初二上学期几何期中考试
 一、填空题:(每小题3分,共30分)
一、填空题:(每小题3分,共30分)
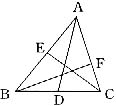
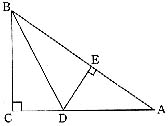
1.已知,如图,AD是△ABC的中线,CE是△ABC的角平分线,BF是△ABC的高,则有:BD=![]() ,∠ =90°,∠ACE=∠ 。
,∠ =90°,∠ACE=∠ 。
2.两根木棒的长分别是8cm,10cm,选择第三根木棒将它们钉成一个三角形。那么第三根木棒长x的范围是 。
3.如果以5cm为等腰三角形的一边,另一边为10cm,则它的周长应为 。
 4.在平坦的草地上,有A、B、C三个小球,若已知A球和B球相距3m,A球和C球相距1m,则B球与C球可能相距
米。(球的半径忽略不计只要求填出一个符合条件的数)
4.在平坦的草地上,有A、B、C三个小球,若已知A球和B球相距3m,A球和C球相距1m,则B球与C球可能相距
米。(球的半径忽略不计只要求填出一个符合条件的数)
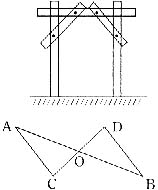
5.木工师傅做完门框后,为防止变形,常常像图中所示那样钉上两条斜拉的木板条,这样做根据的数学道理是 。
6.已知,如图,AB、CD相交于点O,且互相平分,则AC和DB的位置关系是 。
 7.如果两个等腰三角形
,那么两个等腰三角形全等(只填一种能使结论成立的条件)。
7.如果两个等腰三角形
,那么两个等腰三角形全等(只填一种能使结论成立的条件)。
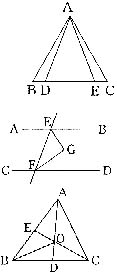
8.如图,△ABD和△ACE中,有下列四个论断:①AB=AC,②AD=AE,③∠B=∠C,④BD=CE,请你以其中三个论断作为条件,余下一个论断作为结论,写出你认为正确的一个命题 。
9.如图,AB∥CD,EG、FG分别是∠BEF与∠EFD的角平分线,交点为G,则∠G= 。
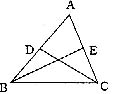
10.如图,已知AD、CE为△ABC的角平分线,连结BO,∠DAC=
30°,∠ECA=35°,则∠ABO的度数为 。
二、选择题:(每小题3分,共27分)
1.根据定义,三角形的角平分线、中线和高都是( )
A.直线 B.线段 C.射线 D.以上都对
2.三角形一边上的高( )
A.必在三角形的内部 B.必在三角形的外部
 C.必在三角形的边上 D.以上三种情况都有可能
C.必在三角形的边上 D.以上三种情况都有可能
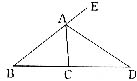
3.如图,AD是∠CAE的平分线,∠B=35°,∠DAE=60°,那么∠ACD等于( )
A.95° B.85° C.60° D.93°
4.下列命题正确的是( )
A.等腰三角形一定不是直角三角形 B.等边三角形一定是等腰三角形
C.等腰三角形一定是锐角三角形 D.直角三角形一定是不等边三角形
5.下列结论名错误的是( )
A.全等三角形对应边上的高相等
B.全等三角形对应边上的中线相等
C.斜边和一个锐角对应相等的两个直角三角形全等
D.两个锐角对应相等的两个直角三角形全等
6.在锐角三角形ABC中,∠A>∠B>∠C,则下列结论错误的是( )
A. ∠B+∠C<90° B. ∠A>60° C. ∠B>45° D. ∠C<60°
7. 下列命题中,逆命题为真的是( )
A.在△ABC中,若∠A的钝角,则∠B、∠C都是锐角
B.如果两个角是对顶角,那么这两个角相等
C.角平分线上的点到角两边的距离相等
D.若x=1,则x(x-1)=0
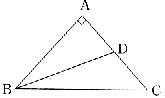 8.如图,△ABC是直角三角形,∠A=90°,BD是角平分线,AD=n,BC=m,则△BDC的面积是( )
8.如图,△ABC是直角三角形,∠A=90°,BD是角平分线,AD=n,BC=m,则△BDC的面积是( )
A.2mn B.mn
C.![]() mn D.
mn D.![]() mn
mn
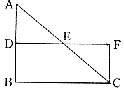
9.如图,已知AB∥CF,DE=EF,AB=15,CF=8,那么DB等于( )
 A.5
B.6
A.5
B.6
C.7 D.8
三、(8分)
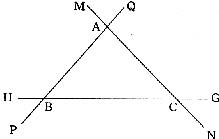
如图,直线MN、GH、PQ表示三条两两相交点A、B、C的公路,现要建一个货物中转站,使该站到三条公路的距离相等,这样的中转站应建军在哪里?符合条件的位置有几个?请用尺规在图中画出供选择的所有位置。
四、解答题:(每小题8分,共16分)
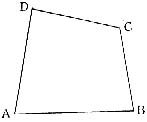
1.如图,草原上的4口油井位于四边形ABCD的4个顶点,现在要建立一个维修站H,试间H建在何处,才能使它到4口油井的距离之和HA+HB+HC+HD为最小,说明理由。
2.在学习“角的平分线”一节的课堂上,老师要求同学们练习一道题,题目是图形如图,图中的BD是∠ABC的平分线,在同学们忙于画图和分析题目时,张小明同学忽然兴奋地大声说:“我有个发现!”原来他感到自己创造了一个在直角三角形中画锐角的平分线的方法,他的方法是这样的:如图,在AB上取点E,使BE=BC,然后画DE⊥AB交AC于D,那么BD就是∠ABC的平分线。
有的同学对张小明的画法表示怀疑,你认为他画得对吗?请说明理由。
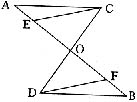
五、(8分)如图,AB与CD相交于点O,且AC∥BD,OC=OD,E、F为AB上两点,且AE=BF,求证:△COE≌△DOF。
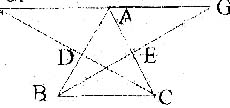
六、(11分)已知△ABC中,延长AC边上的中线BE到C,使EG=BE,延长AB边上的中线CD到F,使DF=CD,连结AF、AG。
 (1)补全图形
(1)补全图形
(2)AF与AG的大小关系如何?证明你的结论。
初二上学期几何期考试答案
一、填空题(每小题3分,共30分)
1.BC AFB(或∠CFB)BCE 2.2cm<x<18cm 3.25cm 4.略 5.三角形的稳定性 6.AC∥BD 7.略 8.略 9.90° 10.25°
二、选择题(每小题3分,共27分)
1.B 2.D 3.A 4.B 5.D 6.A 7.C 8.C 9.C
三、(8分)答:中转站应建在△ABC内部。…………………………2分
符合条件的位置只有一个。……………………………………………4分
作图略(每作一个角的平分线2分)…………………………………8分
四、解答题(每小题8分,共16分)
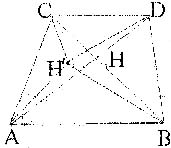 1.解:连结BD AC交点便于工作为H的位置……………………2分
1.解:连结BD AC交点便于工作为H的位置……………………2分
理由:另设不同于点H的另一点H′连结AH′BH′CH′DH′
可得AH′+CH′>AC,即AH′+CH′>AH+CH………………5分
同理:BH′+DH′>BH+DH………………………………………7分
∴HA+HB+HC+HD为最小……………………………………8分
2.解:他的画法是正确的…………………………2分
理由:由题意可知:BE=BC,∠BEF=90°
![]() BE=BC
BE=BC
在Rt△BCD和Rt△BED中
BD=BD
∴Rt△BCD≌Rt△BED ∴∠CBD=∠EBD即:BD为∠ABC的平分线
五、(8分)证明:∵AC∥BD ∴∠A=∠B……………………2分
在△AOC与△BOD中
![]() ∠A=∠B
∠A=∠B
∠AOC=∠BOD ∴△AOC≌BOD ∴AO=BO……4分
OC=OD ∵AE=BE ∴OE=OF……………………6分
![]() CO=DO
CO=DO
在△COE与△DOF中 ∠COE=∠DOF ∴COE≌△DOF……8分
 OE=OF
OE=OF
六、(11分)解:(1)补全图形如图………………4分
(2)AF=AG………………………………5分
证明:∵BE为AC中线 ∴AE=EC
在△AEG与△CEB中AE=EC ∠AEG=∠CEB BE=EG
∴△AEG≌△CEB ∴AG=BC…………………………7分
同理:△ADF≌△BDC ∴AF=BC…………………………9分
∴AF-AG………………………………………………………11分