机密 ★ 启用前
初二数学第二学年末教学质量测试
数 学（非实验区）
本试卷分为试题卷和答题卷两部分，其中试题卷由第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）组成，共4页；答题卷共4页.满分100分.考试结束后将答题卡和答题卷一并交回.
第Ⅰ卷(选择题, 共42分)
注意事项:
1.答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上.
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦擦干净后,再选涂其他答案,不能答在试题卷上.
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的,把它选出填涂在答题卡上.
1.
的平方根是
A.+
B.+2
C.+4
D.4
2.在1.732,-
，π,3.14,2+
,3.…,3.14中无理数有
A.5个 B.2个 C.3个 D.4个
3.商店出售下列形状的地砖:①正三角形;②矩形;③正五边形;④正六边形.若只选购其中某一种地砖镶嵌地面,可供选择的地砖有
A.4种 B.3种 C.2种 D.1种
4.点P是ΔABC中AB上的一点,过点P作直线(不与直线AB重合)截ΔABC,使截得的三角形与原三角形相似,满足这样条件的直线最多有
A.2条 B.3条 C.4条 D.5条
5.已知等腰三角形的两条边长分别为
和
,这个三角形的周长是
A. 
B.
C.或 D.答案都不对
6.若
有意义,则a的取值范围是
A.a≤3且a≠2 B.a<3且a≠2 C.a<3 D.a≤3
7.我国股市交易中,每买、卖一次需各交千分之七点五的各种费用,某投资者以每股10元的价格买入某股票1000股,当该股票涨到12元时全部卖出,该投资者的盈利为
A.2000元 B.1925元 C.1910元 D.1835元
8.以线段a=9,b=10,c=11,d=12为边作四边形,这样的四边形能作
A.0个 B.1个 C.2个 D.无数个
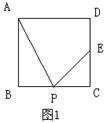
9.如图1,四边形ABCD是正方形,E为DC的中点,P为BC上一
点,则下列条件:①∠APB=∠EPC;②∠BAP=∠CEP;③P是BC的
中点;④BP:BC=2:3,其中能推出ΔABP与ΔECP相似的有
A.4个 B.3个 C.2个 D.1个
10.若数轴上表示数a的点在原点的左边,则化简2a+
的结果是
A.2a B.-3a C.a D.-a
11.若a=
,b=
,则a+b+ab的值是
A. 
B.
C.-5
D.3
12.在线段、角、平行四边形、矩形、菱形、直角梯形、正方形、圆中，既是中心对称图形又是轴对称图形的个数是
A．7 B.6 C.5 D.4
13．梯形ABCD中,AD∥BC,AC与BD交于点O,则ΔAOB和ΔCOD是
A.等积形 B.相似形 C.全等形 D.以上都不对
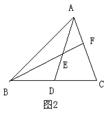
14．如图2，AD是△ABC的中线，E是AD的中点，BE的
延长线与AC交于F，则AF：AC等于
A．
B. 
C.
D. 
第Ⅱ卷(非选择题,共58分)
注意事项:
1. 用钢笔或圆珠笔将答案直接写在答题卷上.
2. 答卷前将答题卷的密封线内项目填写清楚.
二、填空题:本大题共4小题,每小题4分,共16分.把答案填在题中横上.
15.比较大小:
+2 
-2.
16.若x+y=6,xy=4,则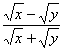
=
.
17.如图3,把一个面积为1的正方形等分成两个面积为
的矩形,接着把面积为的矩形等分成两个面积为
的矩形,再把面积为的矩形等分成两个面积为
的矩形,如此进行下去,试利用图形揭示的规律计算:+++
+
+
+
+
=
18.有一位同学想利用树影测量树高,他在某一时刻测得小树高为1m,树影长为0.9m.但当他马上测量大树影时,因大树靠近一栋建筑物,影子不全在地面上,有一部分影子在墙上,他先测得地面部分的影长BC=2.7m,又测得墙上影高为CD=1.2m,则树高AB为 m.
三、解答题:本大题共6小题,共42分.解答应写出文字说明、证明过程或演算步骤.
19.(本题满分7分)计算: (
-
+
)÷
20.(本题满分7分)化简： 
+(
-
)÷
21.(本题满分7分)最简根式
与
,能否成为同类二次根式?若能,求出x、y的值;若不能,请说明理由.
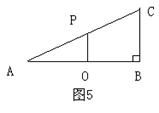
22.(本题满分7分)如图5,在ΔABC中
∠B=90º，AB=4,BC=3,O是AB的中点,
OP⊥AB,交AC于P点.
(1)证明线段OA、OB、OP中,任意两条线段
之和大于第三条线段的长度;
(2)过线段OB(包括端点)上任一点M,作MN⊥AB交AC于点N.如果要使线段AM、MB、MN中任意两条线段之和大于第三条线段的长度，那么请求出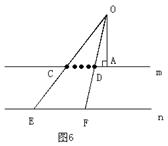
线段AM的长度的取值范围.
23. (本题满分7分)如图6,在一条河的两
岸有一段是平行的,在河岸m上每隔5米有
一棵树,对岸n上每隔50米有一根电线杆.
现在离河岸m处的O点(OA=25米)看对岸n,
发现两根电线杆恰好被河岸m上的两棵树遮
住,并且这两棵树之间还有三棵树,求河宽.
24. (本题满分7分)操作：在正方形ABCD中，点P是CD上一动点（与点C、D不重合），使三角尺的直角顶点与P重合，并且一条直角边始终经过点B，另一直角边与正方形的某一边所在直线交于点E.
(1)观察操作结果，哪一个三角形与ΔBPC相似？并证明.
(2)当点P位于CD的中点时,你找到的三角形与ΔBPC的周长比是多少?