初二数学第二学期期末考试试卷
A卷（100分）
一、专心填一填（每题3分，共39分）
1、64的平方根是 ，立方根是 。
2在π，
，—
，0，12345，2003，
—1这些数中，是无理数的为
3．若∠A为锐角，且sinA=
，则tanA=
．
4．在函数y=
中，自变量x的取值范围是
.
5.在平面直角坐标系中，点P（3，—4）关于y轴的对称点的坐标是 .
6. 己知RtΔABC与RtΔDEF，∠C=90°， ∠F=90°，∠A=67° ∠D=23° 则ΔABC与 ΔDEF （填“相似”或“不相似” ）
7．如图，已知AD是Rt⊿ABC 斜边BC上的高，且AB=6，，BC=10，则AC= ，sinа= .
8．如图，D为AB上一点，只要具备一个条件： ，就可使⊿ACD∽⊿ABC.
9．tan50°×tanа=1,则а= , 4sin260°=
10. 某人沿坡度i=1：的桥向上走50米，这时，他离地面的高度是
米。
11.盒字里装有10颗水果糖、2颗奶糖、3颗巧克力糖，随手拿出一颗，恰好是水果糖的机会是 ，恰好是巧克力糖的机会是 。
12．样本101，98，102，100，99的标准差是
13．边长为2的等边三角形的面积是
二、精心选一选（每题3分，共30分）
| 题号 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 答案 |
14．下列计算正确的是（ ）
A、
=3 B、
=3 C、=±3 D、
=3
15.下列是同类二次根式的是（ ）
A、和
B、和
C、和
D、
和
16. 在RtΔABC中，∠C＝90o，∠A、∠B、∠C所对的边分别为a、b、c，则下列正确的是（ ）
A、
B、
C、
D、
17. 若△ABC∽△A′B′C′，∠A=40°，∠C=110°，则∠B′等于（ ）
A、30° B、50° C、40° D、70°
18.在下列函数中，当x (x > 0) 增大时，y反而减小的函数是( )
A、 y = 
x B、 y= —
C、y= 5 x D、y = 
19.“早穿皮袄午穿纱”是对一天中温度的最佳写照，它的含义是一天中的（ ）
A、最高气温 B、最低温度 C、平均温度 D、温差极大
20. 如图：在△ABC中，
DE∥AC，则DE：AC=（ ）
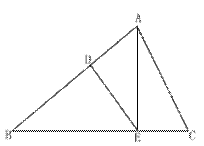
A、8：3 B、3：8 C、8：5 D、5：8
21. 甲、乙两班学生参加了同一次数学考试，班级的均分和方差如下：
则成绩较为整齐的是----------（ ）
A、甲班 B、乙班 C、两班一样 D、无法确定
22．1口袋中有一个红球和2个白球，搅匀后从中摸出第一个球，然后放回口袋，搅匀后摸出第二个球，两次摸的球都是红球的机会是（ ）
A、 
B、 
C、 
D、
23．一个直角三角形的两条边是3㎝和4㎝，则第三边长是( )
A 、5㎝ B 、
㎝
C 、 5㎝或 ㎝ D 、不能确定
三、细心做一做（共31分）
24.（本题10分）计算：（1）2
－9
+4
（2）2sin30°－cot60°+2tan45°
25.（本题6分）在
和
中，已知AB＝7，BC＝5，
试判定与是否相似？请说明理由。
26. （本题6分）某班全体同学在“献爱心”活动中都捐了图书，捐书的情况如下表：
| 每人捐书的册数 | 5 | 10 | 15 | 20 |
| 相应的捐书人数 | 17 | 22 | 4 | 2 |
根据题目中所给的条件回答下列问题：（1）该班的学生共____________名；
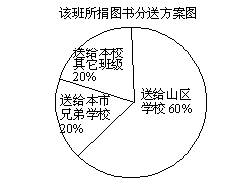（2）全班一共捐了___________册图书；
（3）若该班所捐图书拟按右图所示比例分送给山区学校，本市兄弟学校和本校其它班级，则送给山区学校的书比送给本市兄弟学校的书多________册。
27. （本题9分）在育才中学举行的电脑知识竞赛中，将初三两个班参赛学生的成绩（得分均为整数）进行整理后分成五组，绘制出如下的频数分布直方图（如图）.已知图中从左到右的第一、第三、第四、第五小组的频率分别是0.30、0.15、0.10、0.05，第二小组的频数是40.
(1)求第二小组的频率，并补全这个频数分布直方图；
(2)求这两个班参赛的学生人数是多少；
(3)这两个班参赛学生的成绩的中位数应落在第几小组内（不必说明理由）？
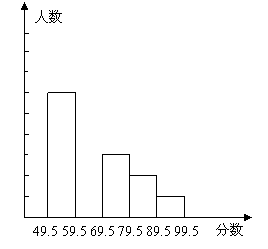
B卷（50分）
四、解答题
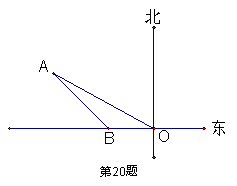28. （本题7分）如图，某轮船在点O处测得一个小岛上的电视塔A在北偏西600的方向，船向西航行20海里到达B处，测得电视塔A在船的西北方向，若要轮船离电视塔最近，则还需向西航行多少海里？（结果保留根号）
29. （本题8分）根据下边给出的调查数据，绘制你认为最恰当的统计图。
调查项目：在互联网上最喜欢做的事情。
| 选项 | 人数 |
| 玩游戏 | 10 |
| 聊天 | 15 |
| 其它 | 25 |
30. （本题9分）甲、乙两名射击运动员在相同条件下各射靶5次，各次命中的环数如下：
甲 5 8 8 9 10
乙 9 6 10 5 10
（1）分别计算每人的平均成绩；
（2）求出每组数据的方差；
（3）谁的射击成绩比较稳定？
31（本题8分）.如图，在⊿ABC中，AD=DB，AE=CE，有一同学发现DE与BC存在以下关系：DE∥BC，DE=
BC。请证明这位同学的结论。
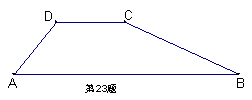
32. （本题8分）如图，一水坝的横断面为梯形ABCD，坝顶DC宽5m，斜坡AD=6m，∠A=600，斜坡BC的坡度i=1：2．求坝底AB的长（精确到0.1m）．(＝1.732, =1.414）
33、提示：此题有A、B、C三道题目， (10分)。
请你根据自已的情况选择其中一道题目给予证明。（多证明的题目不给分）切记：量
|
|
|
力而行，不要勉强噢！
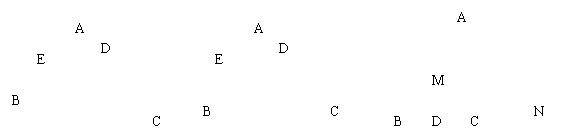
题目A：如图A，已知∠B＝∠C，试说明
。
题目B：如图B，已知
，试说明OB·OD=OC·OE.
题目C：在△ABC中，AD是∠BAC的平分线，M是AD中点，MN⊥AD交BC的延长线
于N，求证：DN2 ＝BN·CN。