| 一、选择题(本题共24分,每小题3分) 下列各题均有四个选项,其中只有一个是正确的。 1、方程x2-4=0的根是( )
A、x1=4, x2=-4 B、x1=2, x2=-2 C、x=4 D、x=2 2、在下列根式中最简二次根式是(其中a>0, b>0)( )
A、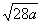 B、 B、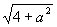 C、 C、 D、 D、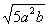 3、当a>3时,化简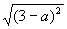 的结果是( ) 的结果是( )
A、a-3 B、3-a C、±(a-3) D、±(3-a) 4、下列图形是轴对称图形而不是中心对称图形的四边形是( )
A、平行四边形 B、菱形 C、正方形 D、等腰梯形 5、能够判断一个四边形是矩形的条件是( )
A、对角线相等 B、对角线互相垂直
C、对角线相等且互相平分 D、对角线相等且互相垂直 6、已知一元二次方程2x2-5x=6的两个根是x1和x2,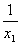 + +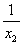 的值是( ) 的值是( )
A、-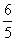 B、 B、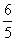 C、- C、-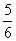 D、 D、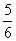 7、两个相似多边形的相似比是2:3,它们的面积之差是30cm2,那么它们的面积之和为( )  A、54cm2 B、76cm2 C、78cm2 D、138cm2 A、54cm2 B、76cm2 C、78cm2 D、138cm2 8、如图,在ΔABC中,AD是BC边上的中线,F是AD上一点,且AF:FD=1:5,连结CF并延长CF交AB于点E,则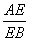 的值是( ) 的值是( )
A、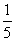 B、 B、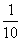 C、 C、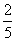 D、 D、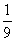 二、填空题(本题共16分,每小题2分) 1、使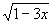 有意义的x值的范围是______________。 有意义的x值的范围是______________。 2、计算:(-2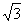 )2=______________. )2=______________. 3、关于x的方程x2-(2k-2)x+k2=0没有实数根时,k的取值范围是______________。 4、关于x的一元二次方程x2-kx-3k=0的一个根是6,那么另一个根是______________。 5、一个凸多边形的内角和是它外角和的2倍,这个多边形是______________边形。 6、已知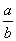 = =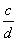 = =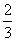 ,且b≠d,则 ,且b≠d,则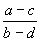 =______________。 =______________。 7、已知梯形的中位线的长为9,下底的长是上底的2倍,则下底的长为______________。 8、在ΔABC中,已知AB=9,AC=12,BC=18,D为AC上一点,DC=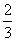 AC,E为AB上一点,若DE截得的三角形与ΔABC相似,则DE的长是______________。 AC,E为AB上一点,若DE截得的三角形与ΔABC相似,则DE的长是______________。 三、计算题(本题共13分,第1、2题每题4分,第3小题5分)
1、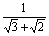 - -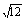 ; ;
2、9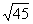 ÷3 ÷3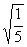 × ×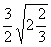 ; ;
3、当x=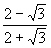 , y= , y=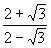 时,求 时,求 + +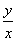 的值。 的值。 四、解方程(本题共17分,第1、2、3小题每题4分,第4小题5分)
1、7x2+2x=0; 2、4(x+3)2=25(x-2)2;
3、2x2=4x+1; 4、x2-m(3x-2m+n)-n2=0(x为未知数) 五、(本题5分)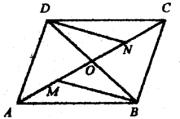 已知:如图,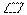 ABCD的对角线AC,BD相交于O点,M是AO的中点,N是CO的中点。 ABCD的对角线AC,BD相交于O点,M是AO的中点,N是CO的中点。
求证:BM//DN,BM=DN。 六、列方程或方程组解应用题(本题6分) 某商场在“五一”假日期间实行让利销售,这样每天所获得的利润恰是销售收入的20%,如果第一天销售收入是4万元,并且每天的销售收入都有增长,第三天的利润是1.25万元。
(1)求第三天的销售收入是多少万元?
(2)求第二天和第三天销售收入平均每天的增长率是多少? 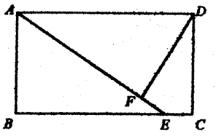 七、(本题6分) 已知:如图,在矩形ABCD中,AB=3,E是BC边上的点,且AE=AD=5,DF⊥AE于点F。
求:EF的长。 八、(本题7分) 已知:如图,△PQR是等边三角形,∠APB=120o. 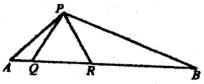
求证:(1)△PAQ∽△BPR; (2)AQ·RB=QR2;
(3)若AQ=2,RB=8,求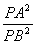 的值。 的值。 九、(本题6分) 已知:如图,在RtΔABC中,∠C=90o, AB=5厘米,BC=a厘米,AC=b厘米(a>b),且a, b是方程x2-(m-1)x+(m+4)=0的两个实根, 求:(1)a和b. 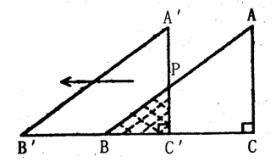
(2)若存在与ΔABC完全重合的ΔA'B'C',在ΔABC不动的条件下,将ΔA'B'C'沿BC所在直线向左以1厘米/秒的速度平移,问几秒种后,两个三角形重叠部分的面积为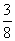 平方厘米。 平方厘米。
初二数学试卷参考答案及评分标准:
一、(本题共24分,每小题3分) | 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | | 答案 | B | B | A | D | C | C | C | B | 二、(本题共16分,每小题2分)
1. x≤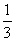 ; 2. 12; 3. k> ; 2. 12; 3. k>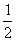 ; 4. -2; 5. 六; 6. ; 4. -2; 5. 六; 6.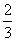 ; 7. 12; ; 7. 12;
8. 6或8. (写对一个给1分) 三、(本题共13分,第1、2小题每题4分,第3小题5分)
1、解:原式=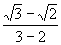 -2 -2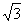 ……………………………………2分 ……………………………………2分
=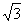 - -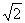 -2 -2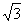 =- =-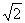 - -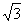 . …………………………4分 . …………………………4分
2、解:原式=(9÷3×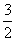 ) )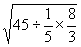 …………………………2分 …………………………2分
=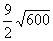 =45 =45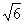 . …………………………………4分 . …………………………………4分 3、解:x=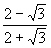 =7-4 =7-4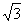 , y= , y=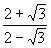 =7+4 =7+4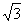 , ………………2分 , ………………2分
x+y=14, xy=1.
 + +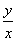 = =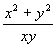 ………………………………………3分 ………………………………………3分
=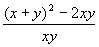 = =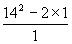 =194. ………………5分 =194. ………………5分 四、(本题共17分,第1、2、3小题每小题4分,第4小题5分) 1、解:原方程变形为
x(7x+2)=0, ……………………………………………………2分
x=0或7x+2=0,
∴x1=0, x2=-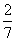 . ………………………………………………4分 . ………………………………………………4分 2、解:原方程变形为
4(x+3)2-25(x-2)2=0, …………………………………………1分
[2(x+3)+5(x-2)][2(x+3)-5(x-2)]=0,
(7x-4)(-3x+16)=0, ……………………………………………2分
7x-4=0或-3x+16=0,
∴x1=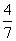 , x2= , x2=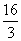 . ………………………………………………4分 . ………………………………………………4分 3、解:原方程变形为
2x2-4x-1=0 …………………………………………………1分
∵a=2, b=-4, c=-1,
b2-4ac=(-4)2-4×2×(-1)=24 …………………………2分
∴x=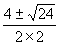 = =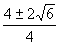 . .
∴x1=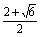 , x2= , x2=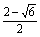 . ……………………………………4分 . ……………………………………4分 4、解:原方程变形为
x2-3mx+(2m2-mn-n2)=0 ……………………………………1分
∵a=1, b=-3m, c=2m2-mn-n2,
b2-4ac=(-3m)2-4×1×(2m2-mn-n2)
=m2+4mn+4n2=(m+2n)2 …………………………3分
∴x=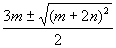 = =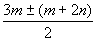
∴x1=2m+n, x2=m-n. ………………………………………5分  五、本题(5分) 证明:连结NB,DM。 ……………1分
∵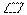 ABCD的对角线AC,BD交于O点, ABCD的对角线AC,BD交于O点,
∴OB=OD,OA=OC. ……………… 2分
∵M是AO的中点,N是CO的中点,
∴OM=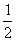 OA,ON= OA,ON=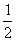 OC。 OC。
∴OM=ON。
∴四边形DMBN是平行四边形。………………………………4分
∴BM//DN,BM=DN。 …………………………………………5分 六、(本题6分) 解:(1)据题意第三天的销售收入是:
1.25÷20%=6.25(万元) …………………………………………1分 (2)设第二天和第三天平均每天的增长率是x, ……………2分
根据题意,得
4(1+x)2=6.25. ……………………………………………………4分
(1+x)2=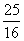 , ,
∴1+x=±1.25,
∴x1=0.25, x2=-2.25(不合题意,舍去)
∴x=0.25=25%. …………………………………………………5分
答:第三天的销售收入是6.25万元;第二天和第三天销售收入平均每天的增长率是25% 。…………………………………………6分 七、(本题6分) 解:连结DE。 …………………………………………………1分
∵矩形ABCD,
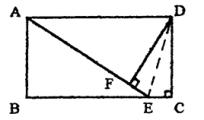 ∴∠B=∠C=90o, AD ∴∠B=∠C=90o, AD BC. BC.
∴∠ADE=∠DEC.
∵AD=AE,
∴∠ADE=∠AED.
∴∠DEC=∠DEF. …………2分
∵DF⊥AE,
∴∠DEF=90o. 在△DFE和△DCE中,
∠DFE=∠C=90o,
∠DEF=∠DEC,
DE=DE,
∴△DFE≌△DCE(AAS). ………………………………………4分
∴EF=EC 在Rt△ABE中,
BE=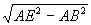 = =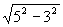 =4, ………………………………5分 =4, ………………………………5分
BC=AD=5,
∴EC=BC-BE=1.
∴EF=1. …………………………………………………………6分 八、(本题7分) 证明:(1)∵△PQR是等边三角形,
∴∠PQR=∠PRQ=∠QPR=60o.
∴∠PQA=∠PRB=120o.
∵∠A+∠APQ=∠PQR=60o.
∠APQ+∠RPB=∠APB-∠QPR=120o-60o=60o.
∴∠A=∠RPB.
∴△PAQ∽△BPR. …………………………………3分 (2)∵△PAQ∽△BPR,
∴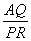 = =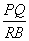 , ,
∴AQ·RB=PQ·PR,
∵PQ=PR=QR,
∴AQ·RB=QR2 …………………………………………5分 (3)∵△PAQ∽△BPR,
∴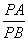 = =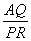 , (1) , (1)
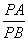 = =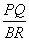 , (2) , (2)
(1)×(2)
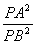 = =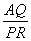 · ·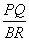 . .
∵PR=PQ,
∴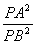 = =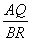 = =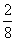 = =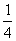 .…………………………………………7分 .…………………………………………7分 九、(本题6分) 解:(1)∵a, b是方程x2-(m-1)x+m+4=0的两个根,且a>b,
∴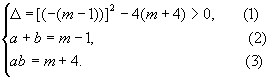 ………………1分 ………………1分
又 在RtΔABC中,∠C=90o, AB=5,
∴ AB2=BC2+AC2,
即 a2+b2=25.
∴ (a+b)2-2ab=25. (4)
将(2), (3)代入(4)式,
得 (m-1)2-2(m+4)=25,
解得m1=8, m2=-4,
但m=-4时,使a+b=-5, 不合题意,舍去.
∴ m=8.
解得a=4, b=3. ………………………………………3分 (2)设A'C′交AB于点P,
∵A'C'//AC, ∴△PBC'∽△ABC.
∴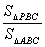 =( =(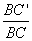 )2. )2.
∵S△PBC=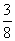 , S△ABC= , S△ABC=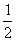 ×3×4=6, BC=4, ×3×4=6, BC=4,
∴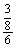 =( =(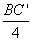 )2. )2.
解得 BC'=±1, BC'=-1 不合题意,舍去.
∴BC'=1, CC'=BC-BC'=3.
由题意可知:3秒后,两个三角形重叠部分的面积为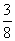 平方厘米。…………6分 平方厘米。…………6分 |