初二数学第二学期期末质检试卷
| 题序 | 一 | 二 | 三 | 四 | 五 | 卷面 | 总分 |
| 得分 |
注意：本卷满分120分，其中书写认真、卷面整洁占2分.
一、填空题（4×10=40）
1． 
的平方根是 ；-27的立方根是 ；
的算术平方根是______.
2.在平面直角坐标系中，点P（－1，2）关于y轴的对称点坐标为 ．
3.函数
中自变量x的取值范围是
．
4.下列各数：
，
，
, 
，
，
，其中无理数有 个.
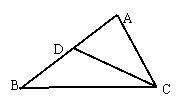
5．如图:D是△ABC的边AB上一点，要使△ABC∽△ACD，还须添加的一个条件可以是__ . (只填一个)
 |
 |  | ||
（第5题） （第7题） （第10题）
6.若点A(7,a),B(3,b)在反比例函数y =
的图象上,则a与b的大小关系是____ _____.
7.如图：一棵大树在距地面5米的C处被台风吹折，折断部分与地面的夹角∠ABC=30º，则大树原来的高度是 米.
8.小明身高是1.5米，他的影长是2米，同一时刻一电线杆的影长是20米，则电线杆的高度是 米.
9.A、B两地相距250千米，一汽车从A地匀速驶往B地，速度是每小时60千米，则汽车和B地距
离y（千米）与行驶时间x（小时）之间的函数关系式是 .(不用求x
的取值范围)
10.如图：Rt△ABC中，∠C=90º, AC=5，AB=13，点P、Q是斜边AB的三等分点，则△CPQ的面积
等于 .
二、选择题 (3×5=15)
11.下列各式中正确的是 （ ）
A.
B.
C.
D.
12.一个布袋里有2个红球和2个白球，先从布袋中摸出一个球，放回后再摸出一个球，则下列事
件中发生的机会最大的是 （ ）
A.两个红球 B.两个白球 C.先红后白 D.一红一白
13.下列图形中一定相似的是 ( )
A. 两个等腰三角形 B. 两个直角三角形
C. 两个矩形 D. 两个正方形
14.Rt△ABC中，∠C=90º,a、b、c分别是∠A、∠B、∠C所对的边，则下列各式中正确的是 （ ）
A. c=a·sinA B. b=c·cosB C. a=b·tanA D. b=a·tanA
15.某人骑车外出，所行路程s（千米）与时间t（小时）的函数关系
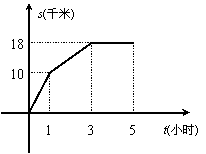如图所示，现有以下四种说法：
① 最初的1小时骑车的速度最快；
② 最初的1小时骑车的速度最慢；
③ 出发后4小时距离起点18千米；
④ 一直骑了5小时，没有休息；
其中说法正确的是 ( )
A．①③ B．②④ C．①④ D．②③
|
三、计算下列各题（2×5=10）
16. 3
＋
—×
17. sin60º•tan30º－cos45º
四、解答题（3×6=18）
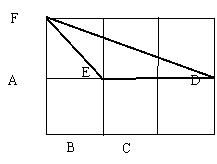
18.如图：在边长为1的正方形网格中，有△ABC和△DEF，它们相似吗？若相似，请说明理由并写出相似比.
 |
 |
19.表一是甲、乙两名射击运动员在选拔赛中的成绩记录表，表二是这次成绩的统计表.
（1）、把统计表补充完整；
表一 表二
| 一 | 二 | 三 | 四 | 五 | 六 | 七 | 八 | 九 | 十 | |
| 甲 | 9 | 6 | 6 | 8 | 7 | 6 | 6 | 8 | 8 | 6 |
| 乙 | 4 | 5 | 7 | 6 | 8 | 7 | 8 | 8 | 8 | 9 |
| 平均数 | 方差 | |
| 甲 | 7 | 1．2 |
| 乙 | 2．2 |
（2）、如果你是教练，你会选择哪位运动员参加正式比赛？请说明理由.
20.某中学部分同学参加初中数学竞赛，指导老师统计了本校所有参赛同学的成绩（成绩都是整数，试题满分120分），并且绘制了“频数分布直方图”（如图）．请回答：
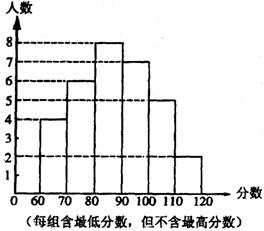(1)该校参加这次数学竞赛共有 名同学；
(2)如果成绩在90分以上（含90分）的同学获奖，那么
该校参赛同学的获奖率约是 ；（精确到1%）
(3)图中还提供了其它信息，例如该中学没有获得满分
的同学等等．请再写出1条信息：
.
五、解答下列各题（5×7=35）
21.
已知直线的解析式为
.
（1）.求直线与y轴的交点A和与x轴的交点B的坐标；
（2）.在右边的方框内建立平面直角坐标系
并画出这条直线；
（3）根据图象回答：当x 时y>0.
| |
 | |||
| |||
23．为发展电信事业，方便用户，A地电信公司对移动电话采用不同的收费方式，其中所使用的“便民卡”和“如意卡”每月(30天)的通话费y（元）与通话时间x(分钟)的关系如图：
 |
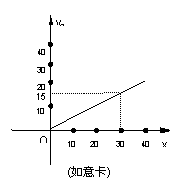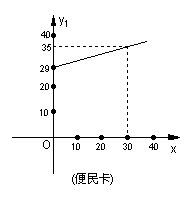
(1)分别求出两种卡每月通话费y1、y2与通话时间x之间的函数关系式.
(2)林小姐决定选用“便民卡”和“如意卡”中的一种.计划每月通话费不超过45元，请你帮助林小姐分析应选哪种卡较合算.
24.如图，在直角△ABC中，∠C＝90°，AC＝4，BC＝3，D为AB上的一点，AD＝2.若点E在AC上，且以A、D、E为顶点的三角形与原三角形相似，试找出所有符合条件的点E，并求出AE的长.
 |
25.如图，四边形DEFG是ΔABC的内接矩形，如果ΔABC的高AH=8cm，底边BC=10cm，设DG=xcm，DE=ycm，
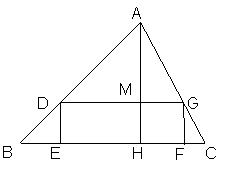(1)求y关于x的函数关系式．
(2)当x=5cm时，求矩形DEFG的面积S.