不等式及不等式组（北师版）
一、选择题
1、不等式组
的解集是（
）
A．－4≤x<1 B．－4<x≤1 C．－4<x≤2 D．－4≤x≤1
2、若ab≠0，则等式a＋b=a＋b成立的条件是（ ）
A．a>0，b>0 B．ab<0 C．a＋b=0 D．ab>0
3、不等式3x－1999≤1的正整数解有（ ）个.
A．669 B．668 C．667 D．666
4、如果关于x的不等式2x＋a≥0的负整数解为－2，－1，那么a的取值范围是（ ）
A．4≤a<6 B．0<a≤2 C．4≤a<5 D．0≤a<2
5、如果不等式
，那么代数式
的值是（
）
A．1或－1 B．1 C．－1 D．0
6、关于x的不等式组
的解集为3≤x<5，则
的值是（
）
A．－2 B．－
C．－4 D．－
7、已知不等式5(x－2)＋8<6(x－1)＋7的最小整数解是方程2x－a=4的解，则a的值是（ ）
A．－6 B．－8 C．－5 D．－4
8、某次数学测验，共有16道选择题，评分办法是：答对一题给6分，答错一题倒扣2分，不答则不扣分，某同学有一道题未答，那么这个同学至少答对多少题，成绩才能在60分以上（ ）
A．11题 B．12题 C．13题 D．14题
9、如果不等式组
的整数解仅为1，2，3，那么适合这个不等式组的整数a、b的有序实数对（m，n）共有（ ）
A．12个 B．64个 C．72个 D．81个
10、长途汽车客运站规定，旅客可随身携带一定重量的行李，如果超过规定，则需要购买行李票，行李费用y（元）是行李重量（千克）的一次函数，如图所示，那么，行李重量x（千克）超过多少千克时就要付行李费（ ）
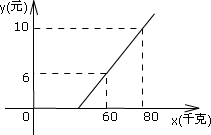
A．25 B．28 C．30 D．35
窗体底端
二、综合题
11、若不等式3(x－1)>2(x＋1)的解都是不等式ax>b的解，问a、b应满足什么条件.
12、小明家的鱼塘中养了某种鱼2000尾，现准备打捞出售，为了估计鱼塘中这种鱼的总质量，从鱼塘中捞了三次，得到的数据如下表：
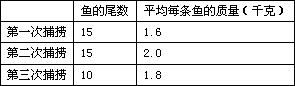
（1）鱼塘中这种鱼平均每条质量约是多少千克，鱼塘中这种鱼的总质量约是多少千克？若将这种鱼不分大小，按每千克7.5元的价格出售，小明家约可收入多少元？
（2）若鱼塘这种鱼的总质量是题（1）中估计的值，现将鱼塘中的鱼分大鱼、小鱼两类出售，大鱼每千克10元，小鱼每千克6元，要使小明家的收入不低于题（1）中估计的收入，问鱼塘中大鱼的总质量应至少有多少千克？
13、某商店先在广州以每件15元的价格购进T血衫100件，又到深圳以每件12.5元的价格购进该商品400件，现定价为x元出售，且获得不小于12%的利润，那么x至少定价多少元时，才能满足以上要求.
14、一家小型放映厅的盈利额y（元）同售票数x之间的关系如图所示，其中保险部门的规定：超过150人时，需缴纳公安消防保险费50元，试根据图象，回答下列问题：
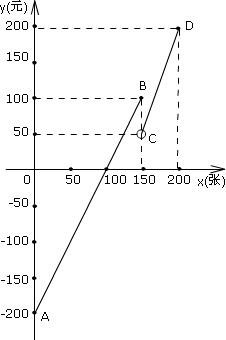
（1）试就0<x≤150和150<x≤200，分别写出盈利额y（元）与x（票数）之间的函数关系式.
（2）当售出票数x为何值时，放映厅不赔不赚？当售出的票数x满足何值时，放映厅要赔本？当售出的票数x为何值时，放映厅能赚钱？
（3）当售出票数x为何值时，此时所获利润较x=150时要多.
答案：一、BDDAC ABBCC
二、11、解：由不等式 3(x－1)>2(x＋1)，得x>5 ① 对不等式 ax>b的解集，要进行讨论.不能认为a必大于零.
（1）当a>0时，x>，∵ x>5的解都是x>的解.
在数轴上表示为：
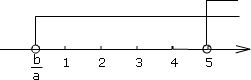∴≤5，∴ b≤5a.
（2）当a=0，且b<0时，ax>b的解集x是一切实数，显然x>5也是ax>b的解. （3）a=0，b≥0时，ax>b无解.
（4）当a<0时，由ax>b，得x<，则不合题意. 综上所述，a，b应满足的条件是a>0，且b≤5a或a=0且b<0.
12、解：（1）依题意，平均每条鱼的质量约为
（千克）
∴ 总质量约为1.8×2000=3600（千克） 可收入7.5×3600=27000（元）
（2）设鱼塘大鱼有x千克，则小鱼有（3600－x）千克. 依题意：10x＋6(3600－x)≥27000，解得x≥1350（千克）.
即鱼塘中大鱼的总质量至少要有1350千克才行.
13、解：若按x元出售，获得不小于12%的利润， ∴ 应满足(100＋400)x≥(15×100＋12.5×400)(1＋12%)
解此不等式，得500x≥6500×
∴ x≥14.56（元）
所以每件T血衫至少按14.56元出售，才能获得不小于12%的利润.
14、解：（1）当0<x≤150时， 线段AB的函数式为（包括A、B两点）y=k1x＋b1，
将点A的坐标（0，－200），B的坐标（150，100）代入， 得到函数式为y=2x－200；
当150<x≤200时， 线段CD（包括点D，但不包括点C）的函数式是y=k2x＋b2，
将点C坐标（150，50）和D的坐标（200，200）代入， 得y=3x－400.
（2）若放映厅若不赔不赚，即盈利y=0，即2x－200=0， ∴ x=100.
若放映厅要赔本，则y<0，即2x－200<0，∴ x<100. 若放映厅要赚，则盈利y>0，即2x－200>0，∴ x>100.
（3）从图象中可看出，当x>100可赚钱，且当x=150时， y=2×150－200=100
即可赚100元钱，要使获利比x=150时要多，则应满足3x－400>100.
∴ x>
≈166.7， 即当售出票数x≥167（张）时，放映厅此时获利比x=150时要多.