八年级数学下综合测试卷(1)
一、选择题（每题3分，共30分）
1. 某市有7万名学生参加中考,要想了解这7万名学生的数学考试成绩,从中抽取了1000名考生的数学成绩进行分析,以下说法正确的是( ) (A) 这1000名考生是总体的一个样本 (B) 每名考生是个体
(C) 7万名考生是总体 (D) 7万名考生的数学成绩是总体
2.甲、乙两班学生参加了同一次数学考试，班级的均分和方差如下：
则成绩较为整齐的是（ ）
（A）甲班 （B）乙班 （C）两班一样 （D）无法确定
3．某地区100个家庭收入按从高到低是5800，……，10000元各不相同，在输入计算时，把最大的数错误地输成100000元，则依据错误的数据算出的平均数比实际平均数多（ ）
（A）900元（B）942元（C）90000元（D）9000元
4.下列命题: (1)相等的角是对顶角. (2) 同位角相等 (3) 直角三角形的两个锐角互余. (4) 若两条线段不相交,则两条线段平行. 其中正确的命题个数有( ) (A) 1个 (B) 2个 (C) 3个 (D) 4个
5. 下列语句不是命题的是 ( ) (A)三角形的三个内角和是180°
(B)角是几何图形 (C) 对顶角相等吗? (D) 两个锐角的和是一个直角
6. 下列图形一定相似的是（ ）
(A)两个矩形 (B)两个等腰梯形
(C)有一个内角相等的两个菱形 (D)对应边成比例的两个四边形
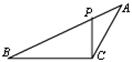
7. 如图，ΔABC中，P为AB上一点，在下列四个条件中：①∠ACP=∠B；②∠APC=∠ACB；③AC2=AP•AB；④AB•CP=AP•CB，能满足ΔAPC与ΔACB相似的条件是（ ） (A)①②③ (B)①③④ (C)②③④ (D)①②④
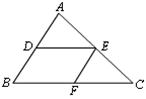
8. 如图，已知DE∥BC，EF∥AB，则下列比例式中错误的是（ ）
(A)
(B)
(C)
(D)
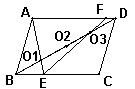
9. 如图,在平行四边形ABCD中,O1、O2、O3分别是对角线BD上的三点，且BO1=O1O2=O2O3=O3D，连接AO1并延长交BC于点E，连接EO3并延长交AD于点F，则AF：DF等于（ ） (A)19:2 (B)9:1 (C)8:1 (D) 7:1
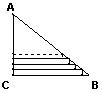
10．某公司在布置联欢会会场时，需要将直角三角形彩纸裁成长度不等的矩形纸条。如图所示：在RT△ABC中，AC=30cm,BC=40cm.依此裁下宽度为1cm的纸条，若使裁得的纸条的长都不小于5cm，则能裁得的纸条的张数 （ ）
(A) 24 (B) 25 (C) 26 (D) 27
二、填空题(共37分)
11. 一个样本的方差是 
，则样本的个数为
,样本的平均数是
.
12. 把命题“等角的补角相等”写成“如果……，那么……”的形式 .
13.某中学初二年级共有400名学生,为了了解这些学生的视力情况,从中随机抽取了50名学生进行测试,若视力为1.0的一组有10人,则该组的频率为 ;若视力为0.8的一组频率为0.3,则该组有 人;根据上述抽样调查可估计该中学初二年级视力为1.0的学生有 人.
14．若
, 则
；若
, 则
；
15. 已知点C是AB的黄金分割点(AC >BC)，若AB=4cm，则AC的长为 。
16. 若
，且a+b+c≠0，则k的值为
.
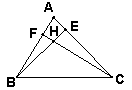
17.在△ABC中,已知∠ABC=66°，∠ACB=54°，BE是AC上的高,CF是AB上的高,H是BE、CF的交点，则∠ABE= ，∠BHC= 。
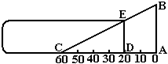
18．如图,测量小玻璃管口径的量具ABC,AB的长为10cm,AC被分为60等份.如果小玻璃管口DE正好对着量具上20等份处(DE∥AB),那么小玻璃管口径DE是 cm。
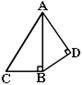
19. 如图，ΔABC与ΔADB中，∠ABC=∠ADB=90°，AC=5cm，AB=4cm，如果图中的两个直角三角形相似，则AD的长= .
20．如图，DE ∥BC，AD = 15 cm , BD = 20cm , AC = 28 cm , 则AE = ；S△ADE:S四边形DBCE= .
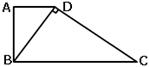
21. 如图，梯形ABCD中,AD∥BC,∠BAD=90°,对角线BD⊥DC, 若AD=4，BC=9，则BD的长= .
22. 如图，ΔABC中，∠C = 
,CD是斜边AB上的高,AD
= 9,BD = 4，那么 CD= ,AC
= .
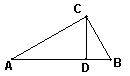
(第19题图) (第20题图) (第21题图) （第22题图）
三、解答题（9分）
23． 甲、乙两位同学本学期11次考试的测试成绩如下：
| 甲 | 98 | 100 | 100 | 90 | 96 | 91 | 89 | 99 | 100 | 100 | 93 |
| 乙 | 98 | 99 | 96 | 94 | 95 | 92 | 92 | 98 | 96 | 99 | 97 |
(1)（4分）他们的平均成绩和方差各是多少？ (2) (2分)分析他们的成绩各有什么特点？
(3)（3分）现要从两人中选一人参加比赛，历届比赛成绩表明，平时成绩达到98分以上才可能进入决赛，你认为应选谁参加这次比赛？为什么？
24．填写推理的依据。(共12分）
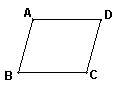
（1）已知：AB∥CD，AD∥BC。求证：∠B=∠D。
证明：∵AB∥CD，AD∥BC（ 已知 ）
∴∠A+∠B=180，∠A+∠D=180°（ ）
∴∠B=∠D （
）
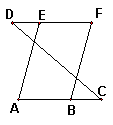
（2）已知：DF∥AC，∠A=∠F。求证：AE∥BF。
证明：∵DF∥AC （已知）
∴∠FBC=∠ （ ）
∵∠A=∠F（已知）
∴∠A=∠FBC （ ）
∴AE∥FB （ ）
四、解答题（每题6分，共12分）
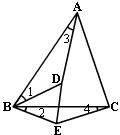
25.如图，D为ΔABC内一点，E为ΔABC外一点，且∠1=∠2，∠3=∠4.找出图
中的相似三角形并说明理由。
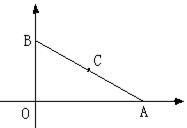
26.如图在平面直角坐标系中，A点坐标为（8，0），B点坐标为（0，6），点C是线段AB的中点。请问在x轴上是否存在一点P，使得以P、A、C为顶点的三角形与△AOB相似？若存在，求出P点坐标(写出计算的过程)；若不存在，说明理由。