八年级数学第二学期期末测试题

八年级数学第二学期期末测试题北师版

一细心选一选（请选择一个你认为最合理的答案，并将答案填写在下面的表格内，每小题 3分，

共30分）

题号	1	2	3	4	5	6	7	8	9	10
答案

， 1. 下列由左边到右边的变形，属于因式分解的是（　 ）

　 A　(x+3)(x -3)=x²-9　　　　　 B　3a²-6a+8=3a(a-2)+8

　 C　- x²- y²+2xy= -(x - y)²　　 C　2a²-4a+1=(2a³-4a²+a)

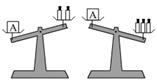2. 如图，在天平盘中的每个砝码的质量都是1g，则物体A的质量m(g)的取值范围，在数轴上可以表示成（　　 ）

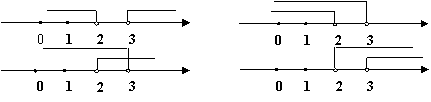A　　　　　　　　　　　　　　　  B

C　　　　　　　　　　　　　　　  D　　　　　　　　　　　　　　　　　　　

（2题图）

3. 电视台要在某地调查某节目的收视率，下列调查方式中最合适的是（　 ）

　A  当地每个看电视的人都调查 　　 B　到当地实验小学调查小学生

　C  在街头随机调查不同行业、不同年龄、不同阶层的几百名市民

　D  调查当地的所有出租车司机

4. 若分式的值为零，则x的值为（　　 ）

　 A　2　　 B　±2　　 C　－2　　　D　0

5. 若≠0，则=（　　　）

A 　　　B 　　 C 　　 D 无法确定

6. 在操场上活动时，小明发现旗杆的影子与旁边的树的影子好像平行，但他不敢确定，

　那么他可以采取的最好的办法是（　 ）

　A 通过平移的办法进行验证　　 B 看看其他同学是不是这样认为

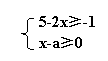  C 构造并测量两个同位角，若相等则影子平行　　D 构造几何模型，用已学知识证明

　　　　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　 

7.　已知关于x的不等式组　　　　　　　  无解，则a的取值范围是（　 ）

　 A　a>3　　　 B　a<3　　 C　a≤3　　 D　a≥3　　

8. 下列说法正确的是（　 ）

　A  数据3、4、3、4、5、5、5、2的众数是3　　

B  为了了解参加运动会的运动员的年龄情况，从中抽取了100名运动员的年龄，在这里100名运动员是抽取的一个样本

C　如果数据x₁ , x₂ ,  …, x_n 的平均数是x ,那么（x₁- x）+（x₂- x）+…+（x_n- x）= 0

D  一组数据的方差为s², 将这组数据中的每一个数都乘以5，得到的一组新数据的方差是5s²

9. 三个同学聚在一起对刚刚结束的甲、乙、丙、丁四个班级的接力赛的成绩进行猜测：李明：甲班第三，丙班是冠军。　赵刚：丙班第二，乙班第三。　王超：丁班第二，甲班是冠军。结果三个人的猜测都只对了一半，则接力赛的成绩顺序应是（　 ）

　 A　乙丙甲丁　　B　乙丁丙甲　　C　丙乙丁甲　 D　丙丁乙甲

10. 已知：如图，△ABC中，AE＝CE，BC＝CD，

那么EF:ED的值是（　 ）

A  2 ׃ 3　　B　1 ׃ 3　  C　1 ׃ 2　　D 3 ׃ 4

二、专心填一填（每空3分，共30分）

　　11．如图2，ABCD的边AD上一点E，DE＝AD，连接CE，交对角线BD于F，则DF∶DB＝________．

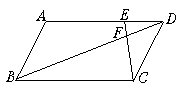
图2

　12．已知一组数据-2，-1，0，x，1的平均数是零，则这组数据的方差是________．

　　13．甲、乙两人比赛飞镖，两人所得平均环数相同，其中甲所得环数的方差为15，乙所得的环数如下：0，1，5，9，10，那么成绩较为稳定的是________(填“甲”或“乙”)．

14．若-2x＋10的值不小于-5，则x的取值范围是_____________．

　

　　15．如图1，在△ABC中，D、E分别在AC、AB上，且AD∶AB＝AE∶AC＝1∶2，BC＝5，则DE＝_______．

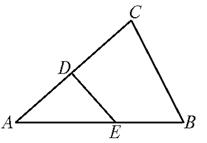
图1

　　

　　16．如图2，在△ABC中，AD是BC边上的中线，BE是AC边上的中线，BE交AD于F，那么AF∶FD＝_______．

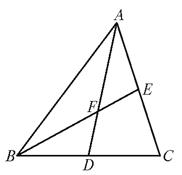
图2

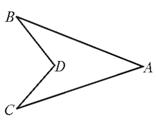
　　17．如图3，∠A＝40°，∠B＝30°，∠BDC＝101°，则∠C＝_______．

18. 科学研究表明，当人的下肢长与身高之比成0.618时，看起来最美，某成年女士身高为153cm，下肢长为92cm，该女士穿的高跟鞋鞋跟的最佳高度约为　　　 cm（精确到0.1cm）

三、解答题（共60分）

 19. 把如图所示的图形放大，使放大前后两个图形的对应线段的比为1:2 。

　　

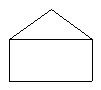
20.

　 （1）解不等式组，并把它的解集表示在数轴上。　　　　( 2 ) 解方程

　　　　　　　　　　　  　　　　　　　　　　　　　　　　　

　　　　

　 （3）请你阅读下列计算过程，再回答提出的问题。

　　 　　　　　　　 （1）左面计算过程中，从哪一步开始出现错误？

=　 （A）　 （2）从B到C是否正确？　

　　= (B)　（3）请你正确解答此题。

= ( x - 3 ) - 3(x+1) 　　　　(C) =  - 2x - 6

　　　　　　　 　　　　　　　　　　　　　　　　

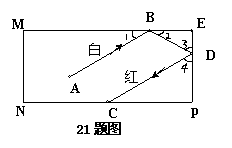
21. 如图所示：长方形台球桌上，选择适当的方向击打白球，使白球两次撞击桌面边缘后将红球撞入袋中，此时，∠1=∠2，∠3=∠4。白球第二次反弹后的方向DC与开始击打白球时的方向AB平行吗？试证明你的结论。答：　　　　　

已知：如图，　　　　　　　　　　　　　　　　　　　　　　　　　　  　　　 

　　　求证：　　　　　　　　　　　　　 　　

22. 某单位将沿街的一部分房屋出租，每间房屋的租金第二年比第一年多500元，所有房屋出租的租金第一年为96 000元，第二年为102 000元。请根据题意提出一个合理的问题：

　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　？

　 并用分式方程进行解答。

　　　　

　　

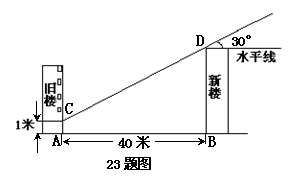23.为解决楼房之间的挡光问题，某地区规定：两幢楼房之间的距离至少40米，中午12时不能挡光。如图23，某旧楼的一楼窗台高1米，要在此楼的正南方40米处再建一幢新楼。已知该地区冬天中午12时阳光从正南方照射，并且光线与水平线的夹角最小为30°，在不违反规定的情况下，新建楼房最高多少米？（结果精确到1米）

　　24．在方格纸中，每个小格的顶点叫做格点，以格点连线为边的三角形叫做格点三角形，请你在图10×10的方格纸中，画出两个相似但不全等的格点三角形，并加以说明．

　　要求：所画的三角形是钝角三角形，并标明相应字母．

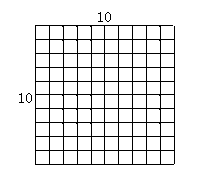
图7

 

 

　　25．为了了解某校九年级300名男学生的身体发育情况，从中对20名男学生的身高进行了测量，结果如下：(单位：厘米)

　　175　161　171　176　167　181　161　173　171　177　179　172　165　157　173　173　166　177　169　181

　　下表是根据上述数据填写的频数分布表的一部分：

分　组	频数累计	频　数	频　率
56.5～161.5		3	0.15
161.5～166.5		2	0.10
166.5～171.5		4	0.20
171.5～176.5	正正		0.30
176.5～181.5	正	5
合　计		20	1.00

　　(1)请填写表中未完成的部分．

　　(2)样本数据中，男生身高的众数是多少？

 

 

　　(3)该校九年级男学生身高在171.5～176.5(厘米)范围内的人数为多少？

 

 

　　(4)根据频数分布表，绘制频数分布直方图．

 

 

　　20．某农科所为了考察两个品种的棉苗生长高度的情况，从甲、乙两种棉苗中各抽出10株，测得它们的株高分别如下(单位：厘米)：

　　甲：27　27　44　16　44　36　38　40　42　30

　　乙：28　46　30　32　44　46　24　18　28　48

　　(1)分别计算两种棉苗的平均苗高．

 

 

　　(2)哪种棉苗长势比较整齐？

 

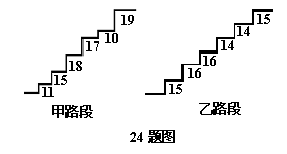24. （10分）在某旅游景区上山的一条小路上，有一些断断续续的台阶，下图是其中的甲、乙两段台阶的示意图，其中的数字表示每一台阶的高度（单位：cm）

（1）两端台阶有哪些相同点和不同点？

（2）那段台阶路走起来更舒服？为什么？

（3）为方便旅客行走，需要重新修整上山的小路，

对于这两段台阶路，在台阶数不变的情况下，

请你提出合理的整修建议。

25. （12分）小华家是某市第一批统一换装“峰谷分时”电表的家庭之一，他们家将率先享受生活用电“峰谷分时电价”的新政策，用电价将按不同时段实行不同的价格：8点至21点为“峰时”，电价为每千瓦时0.55元，21点至次日8点为“谷时”，电价为每千瓦时0.30元。而我市原来实行的电价为每千瓦时0.52元。

（1）　　 小华估计了一下，自己家平时大约每月用电100千瓦时，其中“峰时”用电约占80% 。请你帮小华计算一下，他家原来平均每月需缴电费多少元？实行“峰谷分时电价”后，他家的电费会下降吗？若下降，下降多少元？

（2）　　 小华希望在用电量不变的前提下，改变原来的用电习惯，使他家平均每月的电费能够下降8～12元。假设小华家今后“峰时”用电占整个家庭用电的x% ，那么x在什么范围内时，才能达到小华的期望？