八年级数学
第二学期期中考试试卷2
命题人：于清来
本试卷分A卷和B卷两部分。A卷100分（卷面书写2分），B卷20分，共120分。考试时间120分钟。
A卷 (共100分)
一、填空题（每空2分，共26分）
1．当x＝ 时，分式
无意义．
2．分式
的最简公分母是
．
3．点A（1，6）在反比例函数
图象上，则k＝
，在图象的每一支上，y随x的增大而
（填“增大”或“减小”）．
4．化简
＝
．
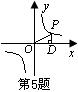
5．点P为反比例函数
的图象上的一点，PD⊥x轴于点D，
则△POD面积为 ．
6．在△ABC中，∠C＝90°，直角边AC＝5cm，BC=12cm，则斜边AB边上的高为 cm．
7．平行四边形ABCD中，∠A＝50°，AB=30cm，则∠C＝ °，DC＝ cm．
8．已知点D，E，F分别为△ABC的边AB，BC，CA中点，连结DE、EF，要使四边形ADEF为菱形，则需要增加的条件是
（只填一个就可以了）．
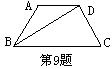
9．如图，在梯形ABCD中，AD∥BC，AB=CD=2㎝, ∠A＝120°，BD平分∠ABC，BD⊥DC，则梯形ABCD的周长为
cm，面积为
cm2．
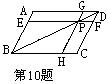
10．如图，在平行四边形ABCD中，EF∥BC，GH∥AB，EF与GH交点P在BD上，图中有 对平行四边形的面积相等．
二、选择题（每小题3分，共24分）
11．在式子
中是分式的个数有（ ）
A．2 B．3 C． 4 D．5
12．如果把分式
中的x和y都扩大3倍，那么分式的值（ ）
A．扩大为原来的3倍 B．缩小为原来的
C．不变 D．缩小为原来的
13．下列等式成立的是 （ ）
A． 
B．
C． 
D．0.=1.68×10-4
14．以下列线段a，b，c的长为三边的三角形中，不能构成直角三角形的是 （ ）
A．a：b：c=1：
：2
B．
C．a=9，b= 40，c=41， D．a=11，b=12，c=13
15．下列命题中正确的是 （ ）
A．对角线相等的四边形是矩形 B．对角线互相平分的四边形是平行四边形
C．对角线互相垂直的四边形是菱形 D．对角线互相垂直且相等的四边形是正方形
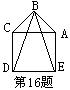16．如图，以等边△ABC的AC边为边，向形外作正方形ACDE，下列结论：
①∠DBE=30°，②BE=BD，③∠BCD=105°，④∠BAE=150°，
其中正确的个数是 （ ）
A．1个 B．2个
C．3个 D．4个
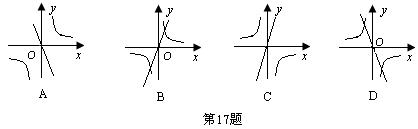17．在同一直角坐标系中，函数
的图象大致是
（ ）
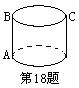18．如图，一有上、下底面的圆柱体纸筒，底面周长为24cm，高AB为5cm，一只蚂蚁从A出发沿着圆柱体的表面爬到点C的最短路程大约是
（ ）
A．12.6cm B．13cm
C．9.1cm D．24.5cm
三、解答题（本题共4小题，共20分）
19．（本题共2小题，共8分）计算
（1）
（2）
20．（本小题4分）先化简
，再选择使等式有意义而你喜欢的数代入求值．
21．（本小题5分）
解方程
22．（本小题3分）
在数轴上作出表示
的点（要求用尺规作图，保留作图痕迹，不要求写作法）．
四、解答题（本题共3小题，共16分）
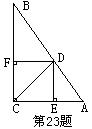
23．（本小题5分）如图，在Rt△ABC中，∠ACB＝90°，CD平分∠ACB， DE⊥AC，
DF⊥BC，垂足分别为E、F．试证明四边形DECF是正方形．
24．（本小题6分）在压力不变的情况下，某物体承受的压强P（Pa）是它的受力面积S（cm2）的反比例函数．请填写下表并回答问题：
| 压强P（Pa） | … |
| 400 | 300 | … |
| 受力面积S（cm2） | … | 0.2 | 0.3 |
| … |
（1）求P与S之间的函数关系式；（2）求当S=0.8 cm2时，物体承受的压强P．
25．列方程解应用题（本小题5分）
甲、乙两种机器人都被用来搬运化工原料，甲型机器人比乙型机器人每小时多搬运30kg，甲型机器人搬运900 kg所用时间与乙型机器人搬运600 kg所用时间相等，两种机器人每小时分别搬运多少化工原料？
五、解答题（本小题共2小题，共12分）
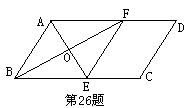26．（本小题5分）如图，在平行四边形ABCD中，∠A的平分线与BC边相交于E，∠B的平分线与AD边相交于点F．（1）求证：四边形ABEF是菱形；（2）如果∠ABC=60°，AB=2．求BF的长．
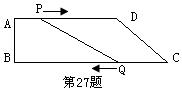
27．（本小题7分）如图，四边形ABCD是直角梯形，∠B=90°，AB=8cm，AD=24cm，BC=28cm，点P从A出发，以1cm/s的速度向D运动，点Q从C同时出发，以3cm/s的速度向B运动．其中一个动点到达端点时，另一个动点也随之停止运动．设运动时间为ts．
（1）当t=7时，四边形ABQP是什么形状的四边形？并证明你的结论．
（2）当t为何值时，线段PQ=10cm．
B卷（共20分）
一、填空题（1—2每小题2分， 3—4小题3分，共10分）
1．顺次连结菱形四边形中点所得的四边形是 ．
2．如图，梯形纸片ABCD，∠B＝60°，AD∥BC，AD=AB=2，BC=6，将纸片折叠，使点B与D重合，折痕为AE，则CE= ．
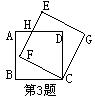3．边长为3的正方形ABCD绕C点按顺时针方向旋转30°后，得到正方形EFCG，EF交AD于点H，那么DH= ．
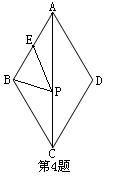
4．如图，在菱形ABCD中，AB=2，∠BAD＝60°，E是AB的中点，P是对角线AC上任一动点，则PE+PB的最小值是 ．
二、解答题（本小题2小题，共10分）
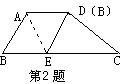
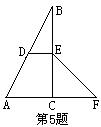
5．（本小题4分）在△ABC中，∠ACB＝90°，DE是△ABC的中位线，点F在AC延长线上，∠B=∠CEF，求证：四边形ADEF是等腰梯形．
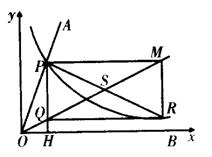
6．（本小题6分）如图，将给定的锐角∠AOB置于直角坐标系中，边OB在x轴上，边OA与反比例函数
的图象交于P点，在反比例函数图象上另取一点R，使PR=2OP，分别过P和R点作x轴与y轴的平行线，两直线交于点M，连结OM，交PR与点S．
（1）设
，求直线OM对应的函数表达式（用含a，b的代数式表示）．
（2）过点P作PH∥ y轴，与x轴交于H点，过点R作RQ∥x轴，与PH交于Q点．
①说明Q点在直线OM上；②请你写出∠MOB与∠AOM的数量关系式，并证明你的结论．
