八年级数学第二学期期中考试试卷
考生注意：1、本卷考试时间120分钟,满分150分；
2、请在密封线内填写清楚班级、姓名、学号；
3、请不要在密封线内填写答案；
4、本卷适用班级是八(1-24)班。
| 题 号 | 1-12 | 13-20 | 21-22 | 23-26 | 27-29 | 总成绩 |
| 得 分 |
| 得 分 | 评卷人 |
一、精心选一选（本大题共12题，每小题3分，计36分 ）
在每小题给出的四个选项中，只有一个是符合题目要求的。请把正确的选项的字母代号填入下表中相应的题号下面。
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
1．如果a＞b ，下列各式中不正确的是 （ ）
A．a－3＞b－3 B．-2a＜-2b C．
＞
D． 
＜
2．下列分式中是最简分式的是 ( )
A.
B.
C.
D.
3．下列不等式解法正确的是 （ ）
A .如果
，那么
． B. 如果
，那么
．
C .如果
，那么
． D. 如果
，那么
4．
（ ）
A．
B.
C.
D.
5.若分式
中的x、y的值都变为原来的3倍，则此分式的值 （ ）
A.不变 B.是原来的3倍 C.是原来的
D.是原来的
6．已知反比例函数的图像经过点（
，
），则它的图像一定也经过 （ ）
A.(－,－) B.(,－) C.(－，) D.（0，0）
7.下列不等式组中，无解的是 （ ）
A.
B.
C. 
D. 
8.一根蜡烛经凸透镜成一实像，物距u，像距v和凸透镜的焦距f满足关系式：＋ = ．若u =12㎝，f =3㎝，则v的值为 （ C ）
A．8㎝ B．6㎝ C．4㎝ D．2㎝
9.如果反比例函数
的图像经过点（－3，－4），那么函数的图像应在（ ）
A. 第一、三象限 B.第一、二象限 C.第二、四象限 D.第三、四象限
10.不等式组
的解集是
，那么
的取值范围是 （ ）
A．
B．
C．
D．
11.若分式
的值为零，则x等于
（ ）
A.0 B.1 C.
D.－1
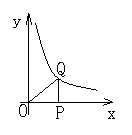
12. 如图,点P是x轴上的一个动点,过点P作x轴的垂线PQ
交双曲线于点Q,连结OQ, 当点P沿x轴正半方向运动时,
Rt△QOP面积 ( )
A.逐渐增大 B.逐渐减小 C.保持不变 D.无法确定
| 得 分 | 评卷人 |
二、细心填一填（本大共8题，每小题4分，计32分）
13.写出一个不等式，使它的解集是x>-3：
14.当x
时，式子
有意义。
15.对于函数
，当时,
随
的 而减小
16.不等式组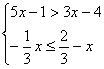
的整数解的和是
.
17.化简
的结果为
18.设有反比例函数
，
、
为其图象上的两点，若
时，
，则
的取值范围是___________
19.不等式-
<1-2x<3的解集是______________.
20.若
求
的值是______________.
| 得 分 | 评卷人 |
三、耐心解一解（本大题共4题，每小题6分，计24分）：
21.解下列不等式(组),并分别将它们的解集在数轴上表示出来．
（1） 
（2）
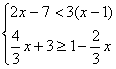
22.计算
(1) 
（2）
| 得 分 | 评卷人 |
四、开心答一答（本大题共8题，第23-26每题7分，第27题8分，第28题10分，第29题12分，计58分）：
23.解分式方程
24.试求当m满足什么条件时，关于x、y的方程组
的解x、y都是负数？
25.先化简再求值
求
的值,其中a=5,b=-2
26.如图，一次函数
的图像与反比例函数
的图像相交于A、B两点，
（1）利用图中条件，求反比例函数和一次函数的解析式
（2）根据图像写出使一次函数的值大于反比例函数的值的的取值范围；
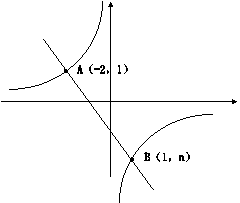
27.某城市平均每天产生垃圾500吨，由甲、乙两个垃圾处理厂处理.已知甲厂每小时可处理垃圾35吨，需费用350元；乙厂每小时可处理垃圾15吨，需费用180元.
（1）甲、乙两厂同时处理该城市的垃圾，每天需几小时完成？
（2）如是规定该城市每天用于处理垃圾的费用不超过5400元，甲厂每天处理垃圾至少需要多少小时?
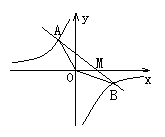28.如图,已知一次函数y=kx+b的图象与反比例函数y=
的图象交于A、B两点, 且点A的横坐标和点B的纵坐标都是-2,求:
(1)一次函数的解析式;
(2)△AOB的面积.
29．国泰玩具厂工人的工作时间：每月25天，每天8小时．待遇：按件计酬，多劳多得，每月另加福利工资100元，按月结算．该厂生产A、B两种产品，工人每生产一件A种产品，可得报酬0．75元，每生产一件B种产品，可得报酬1．40元．下表记录了工人小李的工作情况：
| 生产A种产品件数(件) | 生产B种产品件数(件) | 总时间(分) |
| l | 1 | 35 |
| 3 | 2 | 85 |
根据上表提供的信息，请回答下列问题：
(1)小李每生产一件A种产品、每生产一件B种产品，分别需要多少分钟?
(2)如果生产各种产品的数目没有限制，那么小李每月的工资数目在什么范围之内?