八年级数学第一学期期末考试试卷(模拟二)
班别___________姓名___________学号__________
一、填空题（每题2分，共20分）：
1、在2.3，
，
,
，
，0，
中，其中是无理数的有
。
2、已知
ABCD中，AB=3，AC=BD=6，那么ABCD的面积= ___ 。
3、已知正方形的对角线长为
（
），则它的面积为 __________ 。
4、估算：
（保留两位小数）。
（保留一位小数）。
5、如图的平行四边形ＡBCD中，__________可由线段BA平移后得到，线段OD可以看作是由线段OB__________。
6、一次函数
的图象经过第___________象限，与
轴的交点的横坐标为 ____ ，
的值随的减小而 ___ 。
7、若数据
，0，6，，
，6的平均数为2，则x =_________。数据1，4，2，7，4，4，2，2，3，5的中位数为_________，众数是__________。
8、用正六边形密铺时，每个接点处有_____ 角，每个角的度数为__________。
9、点A关于y轴对称的点B的坐标为（2，-3），则与A关于原点对称的点C的坐标为 。
10、设四边形的各顶点坐标为
，若将该四边形沿着x轴的方向压缩为原来的一般，再向上平移2个单位，那么四边形的各顶点坐标为
。
二、选择题：（每小题2分，共20分）
11、算术平方根等于它本身的数是（ ）
A、0 B、1，0 C、0, 1 ,－1 D、0, －1
12、菱形具有而矩形不一定具有的特征是（ ）
A、对边相等 B、对角相等 C、对角线互相垂直 D、对角线相等
13、点P在第三象限，则点P关于x轴对称的点A在（ ）
A、第一象限 B、第二象限 C、第三象限 D、第四象限
14、下列说法不正确的是（ ）
A、 中心对称图形一定是旋转对称图形
B、轴对称图形一定是中心对称图形
C、在中心对称的两个图形中，连结对称点的线段都被对称中心平分
D、在平移过程中，对应点所连的线段也可能在一条直线上
15、正三角形ABC绕其中心至少要旋转_______度才能与自身重合？（ ）
A、30 B.60 C.180 D.120
16、当k<0，b<0时，一次函数的图像不经过的象限是（
）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
17、小明平时的数学成绩为72分，期中成绩50分，期末为88分，若将平时成绩、期中成绩和期末成绩按1：3：4的权重来计算个人的学期成绩，那么小明的学期成绩为（ ）
(A) 70分 (B) 71.75分 (C) 71.25分 (D) 72分
18、一个长方体的长、宽、高分别为6，4，5,则长方体内所能容下的最长木棒为（ ）
A．
cm
B．
cm
C．7cm
D．
cm
19、下列四个说法中错误的是（ ）
A、两条对角线互相垂直且相等的四边形是正方形
B、菱形的一条对角线平分一组对角
C、顺次连结矩形的各个内角平分线与矩形的交点所围成的四边形是正方形
D、等腰梯形的两条对角线相等
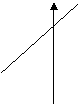
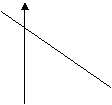
20、已知方程kx+b=0的解是x=3，则函数y=kx+b的图象可能是（ ）
 | |||||||
 | |||||||
 | |||||||
| |||||||
 |  | | |||||
| |||||||
A B C D
三、计算题（共10分）
21、（3分）
22、（3分）
23、（4分）
四、解方程组（共16分）
24、（5分）解方程组
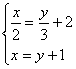25、（5分） 解方程组
 |
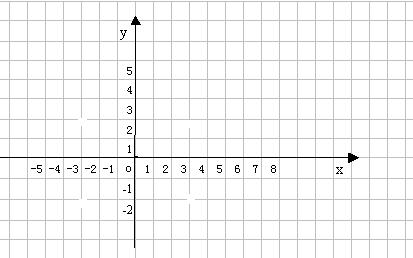26、（6分）利用图象解方程组
五、解答题（共34分）
27、（5分）一艘船由于风向的原因先向正东方向航行了160千米，然后向正北方向航行了120千米，这时它离出发点有多远？
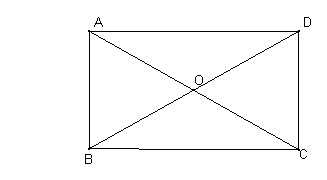28、（6分）如图，已知平行四边形ABCD的对角线AC，BD相交于点O，△AOB是等边三角形，AB＝4cm。平行四边形是矩形吗？请说明理由。
29、（5分）A、B两地相距80千米，一艘船从A出发，顺水航行4时到B，而从B出发逆水航行5时到A，求船在静水中的速度和水流速度？
30、（6分）已知一次函数
的图像与正比例
的图象相交于点（1，2），并且与轴交点的纵坐标为，分别求这两个函数的解析式。
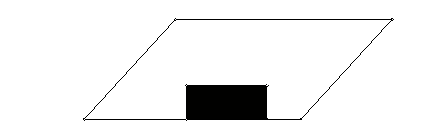31、（5分）在一块平行四边形的稻田内部有一块矩形的水池（阴影部分），现要从池的一边引出一条水渠，将稻田平均分成面积相等的两部分，请你设计一种方案，画出图形，并简单说明画法。
32、（7分）如图：L甲、L乙分别表示甲走路与乙骑自行车（在同一条路上）行走路程y（4米）与时间x（时）之间的关系，观察图象，并回答下列问题。
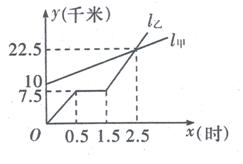(1)乙出发时与甲相距_______________千米.
(2)走了一段路后,乙自行车发生故障停下车修
理修车时间为 时
(3)乙从出发起,经过 时与甲相遇.
(4)求甲行走路程y(千米)与x(时)的函数关系式.