八年级
数学科下学期期中试卷
（考试时间：120分、总分：150分）
一、填空（每空2分，共60分）
1、 9的平方根是 ；4的算术平方根是 ；－8的立方根
是 。
2、计算：
（1）
＝ ； （2）（
）2＝ ；
（3）
＝ ； （4）（1＋
）（1－）＝ ；
（5）
．
＝
3．比较大小：－
－（用“＞”或“＜”或“＝”填空）
4．用计算器计算： 3
－2
≈ （精确到0.01）
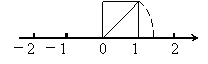5．如图所示：以数轴的单位长度线段为 边作一个正方形，以数轴原点为圆心、正方形对角线为半径画弧交数轴于点A，该图可以说明
6．函数y=
自变量x的取值范围是
7．点P（2，－3）在第 象限，它到x轴的距离为 ，点P关于y轴的对称点坐标是 ，点P关于原点的对称点坐标是 。
8．反比例函数y＝
，当x=－2时，y＝1；
则当y＝－1时，x＝
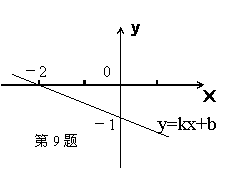
9．根据右图函数的图象填空
（1）当x= 时，y=0；
（2）当x 时，y>0；
10．根据下面图象回答：
y=2x－2
x=_____
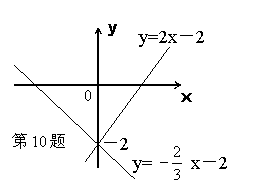方程组 y=－
x－２ 的解是
y=______
11．如上图，已知等腰直角形ABC的直角边长与正方形MNPQ的边长均为20cm，AC与MN在同一直线上，开始时A与M重合，让△ABC以每秒2cm的速度向右运动，最后点A与点N重合。试写出在运动过程中△ABC与正方形MNPQ重叠部分的面积y（cm2）运动时间x（秒）之间的函数关系式是 ，其自变量x的取值范围是 ，重叠部分的最大面积是 cm2。
12．学校平面图的比例尺是1：500，平面图上初中部教学楼与办公楼的距离是6 c
m，则教学楼与办公楼之间的实际距离是_________m 。
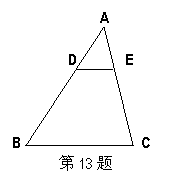
13．如图，△ABC中DE∥BC且
＝
，则
（1）△ADE∽ （2）
＝
（3）若△ADE的面积为1，则四边形BCED的
面积为
 |
14．△ABC∽△A′B′C′，其相似比为2：3，AD、A′D′
分别是对应高，则
＝
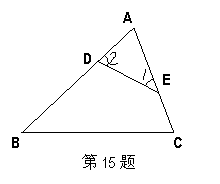
15．如图，请你添加一个条件使△AED∽△ABC，
你添加的条件是
（只需填写一个）
16．请你认真观察、分析、寻找规律：
（1）
＝22，（2）
＝333，
（3）
＝4444，……
由此猜想：
＝
二、选择（每题3分，共27分）
17．下列说法正确的是（ ）
A、0的平方根是0 B、－1的平方根是－1
C、（－3）2的算术平方根是－3 D、－1的立方根是±1
18．在实数－
，0，，3.14, 
，π，0.…，3，中属于无理数的有（ ）个
A、2个 B、3个 C、4个 D、5个
19．已知A（－1，y1）、B（－2，y2）是反比例函数y＝－
上的点，则y1与y2的大小关系是（ ）
A、y1 > y2 B、y1= y2 C、y1 < y2 D、不能确定
20、下列计算正确的是（ ）
A、2＋＝2 B、
－ ＝
＝
C、5
＋5
＝5 
D、5 －4 ＝
21、如图，点D是直角△ABC的斜边AB上一点，过点D画线段DE，使点E在△ABC的边上，并且点D、E和△ABC的一个顶点组成的小三角形与△ABC相似，则满足条件的点E有（ ）
A、2个 B、3个 C、4个 D、5个
22、下列说法正确的是（ ）
A、所有矩形都相似 B、所有的等腰三角形都相似
C、所有菱形都相似 D、所有的等腰直角三角形都相似
23、具有下列条件的两个三角形不一定相似的是（ ）
A、∠A＝40°，∠B＝60°；∠A′＝40°，∠C′＝60°
B、∠A＝60°，AB＝5，AC＝6；∠A′＝60°，A′B′＝15，A′C′＝18
C、∠A＝60°，AB＝3，BC＝4；∠A′＝60°，A′B′＝6，B′C′＝8
D、AB＝3，AC＝5，BC＝7；A′B′＝9，A′C′＝15，B′C′＝21
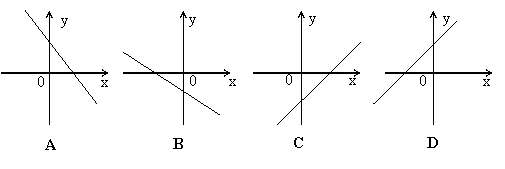
24、一次函数y=kx+b，其中b<0且y随x的增大而减少，则其图象大致是（ ）
| x | 1 | 2 | 3 | 4 |
| y | 2. 02 | 4. 91 | 8. 01 | 11. 02 |
25、某探究性学习小组为了研究某种树木的生长情况，连续几年测得树干直径的数据如下：（y表示树干直径，单位cm；x表示年份），则y与x的函数关系最接近于函数（ ）
A、y=2x B、y=2x2＋1 C、y=3x－1 D、y=2 . 02x
三、解答题
26、计算题（每题6分，计12分）
（1）＋2
－
（2）
·
－
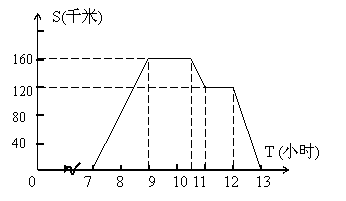
27、（10分）一天上午,李老师从学校出发，乘车去省城开会。返回时，顺路去看望一位朋友，然后返回学校。下图是据此情况画出的图象，请回答下列问题。
（1）李老师是______
点钟离开学校的。
（2）李老师在朋友家待了______小时。
（3）学校离省城开会地大约是________千米。
（4）李老师朋友家距省城开会地是________千米。
（5）李老师在一段路中的车速最快？
答：____________________________
28、（8分）已知直线y=Kx+b与x轴的交点是（，0），且它是由直线y=－3x平移而得到的
（1）求此直线的解析式并画出图象；
（2）求此直线与坐标轴围成的三角形面积；
（3）求直线上与y轴的距离为2的点的坐标。
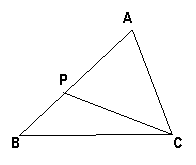29、（8分）如图P是△ABC的边AB上一点，且∠ACP＝∠B。
（1）试说明△ACP∽△ABC；
（2）若AP＝1，BP＝3，求AC的长。
30、（12分）某市为建设节约型社会，鼓励居民节约用水，对民用自来水收费如下规定：每户每月用水不超过5吨按每吨1.20元收费，超过部分按每吨2元收费：
（1）试写出每户月应交水费y（元）与月用水量x（吨）的函数关系式。
（2）若小明家月用水4吨，试求小明家该月应缴的水费是多少？
（3）若小伟家某月缴交的水费为12元，问小伟家该月共用水多少吨？
31、（13分）某公司要印制宣传材料，甲印刷厂表示：每份材料收1元印制费，另收1500元制版费（不考虑单双面制版）；乙印刷厂表示：每份材料收2. 5元印制费，不收制版费。
（1）分别写出两厂的收费y甲、y乙（元）与印制数量x(份)之间的函数关系式并写出自变量x的取值范围。
（2）在同一直角坐标系中，画出题（1）中两个函数的图象。
（3）根据题（2）中的图象回答下列问题：
①若公司拟用3000元印制宣传材料，找哪家印刷厂印制的宣传材料会多一些？
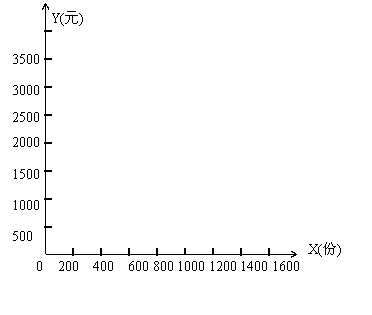②如果某公司计划在甲、乙两印刷厂选择一家印刷一定数量的宣传材料，请你为该公司提供一个合理化选择方案，使每次印制费用支出最省。
附加题：（共10分）
友情提示：请同学们做完上面考题后，再认真检查一遍，估计一下你的得分情况，如果你全卷得分低于90分（及格线），则本题的得分将计入全卷总分，但计入后全卷总分不超过90分；如果你全卷得分已达到或超过90分，则本题的得分不计入总分。
1、（5分）学校请初二同学为校文艺活动制作1000朵小红花，则完成的天数y与该班同学每天能制作的朵数x之间的函数关系式为
2、（5分）已知：如图△ABC∽△DEF，相似比为2：1，若△ABC的三边分别为9cm、12cm、15cm，则△DEF的周长为 cm
 |