八年级数学练习题

八年级数学练习题

（满分100分，90分完卷）

一、选择题：（每小题3分，共30分）

1、在实数，0.6，，，3.14 ，0，中，无理数有（　　 ）。

（A）1个　　　　　　　 （B）2个　　　　　　　　　（C）3个　　　　　　　　 （D）4个

2、若两个等边三角形的边长比为2：3，它们的面积和是78cm²，则这两个等边三角形的面积差是（　　 ）。

（A）16cm²　　　　　　 （B）24cm²　　　　　　　 （C）30cm²　　　　　　　 （D）54cm²

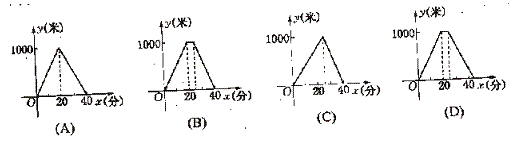
3、小明的妈妈晚饭后出去散步，从家中走20分钟到达离家1000米的万绿园，恰好遇见邻居张大妈也在此散步，就与张大妈聊了5分钟，然后用15分钟返回家里。下面图形中，表示小明妈妈离家的时间与距离之间的关系的是（　　 ）。

4、函数中自变量x取值范围是（　　 ）。

（A）x≥1　　　　　　　　　　　　　　 （B）x≠3

（C）x≥1且x≠3　　　　　　　 （D）x≥1或x≠3

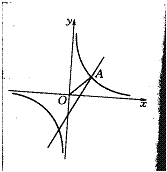
5、对反比例函数，当x₁＜0＜x₂＜x₃时，其对应函数值y₁,y₂,y₃的大小关系是（　　 ）。

（A）y₃＞y₁＞y₂　　　　　　　　　 （B）y₃＞y₂＞y₁

（C）y₁＞y₃＞y₂　　　　　　　　　　 （D）y₂＞y₁＞y₃

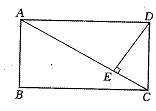
6、如图，在矩形ABCD中，DE⊥AC，设∠ADE=a，

且cos a=，AB=4，则AD的长为（　　 ）。

（A）4.5　 （B）5　 （C）　　　　　　 （D）6

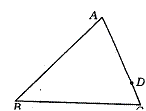7、如图，在△ABC中，AB=24，AC=18，D为AC上

一点，且AD=12，在AB上取一点E，使得以A、D、E为

顶点的三角形与△ABC相似，则AE的长应为（　　 ）。

（A）16　　　　　　　　　　　　　　　　（B）14

（C）16或14　　　　　　　　　　　（D）16或9

8、张老师有4件不同的衬衣和4条不同花色的领带，他要把领带和衬衣搭配，可以有（　　 ）种不同的配法。

（A）12　　　　　 （B）16　　　　　　　（C）8　　　　　　　 （D）4

9、一次函数y= -3x+2的图象与坐标轴交于A、B两点，则A、B两点间的距离为（　　 ）。

（A）　　　　　 （B）　　　　　　　（C）　　　　　　　 （D）

10、“早穿皮袄午穿纱”是对一天中温度的最佳写照，它的含义是（　　）。

（A）一天中的温度气温　　　　　　　　　（B）最低温度

（C）平均温度　　　　　　　　　　　　　　　　　（D）温度极差

二、填空题：（每小题3分，共24分）

1、将直线y= -3x+2向下平移3个单位，得到的直线为　　　　　　  ，y随x的增大而　　 　　 。

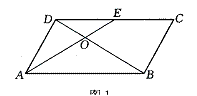
2、如图，平形四边形ABCD中，E为DC的中点，

AE交BD于点O，S_△DOE=12cm²，则平形四边形ABCD的

面积是　　　　 。

3、实数a、b在数轴上如图所示，

化简：　　　　 。

4、若（x-1）³=8，则x=　　　　  。

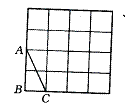5、如图3，在4×4的正方形方格中，△ABC的顶点A、B、C分别在小正方形的顶点上，请在图中画△A₁B₁C₁，使△A₁B₁C₁∽△ABC（相似比不为1），且点A₁、B₁、C₁都分别在小正方形的顶点上。

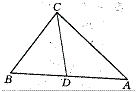6、一艘船向东航行，上午8时到达B处,看到有一灯塔在它的北偏东60°，距离为72海里的A处，上午10时到达C处，看到灯塔在它的正北方向，则这艘船航行的速度为　　　　 。

7、如图，D为AB上的一点，只要具备一个条件（选一

个你认为适当的条件）　　　　  ，就可使△ACD∽△ABC。

8、甲、乙两人在一次射击比赛中的成绩（命中的环数）如下：

甲：9　6  7　6　2  7　7　9  8　9

乙：2　4  6　8　7  7　8　9  9　10

请你通过计算成绩比较稳定的是　　　　 。

三、解答题：（1—4小题，每小题6分；5—6小题，每小题7分；7小题8分）

1、计算：

2、计算：sin²60°+cos²60°-tan30°·cot30°-sin45°·tan45°.

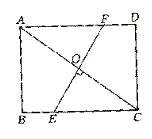3、矩形纸片的长为8cm，宽为6cm，把纸片对折，使相对顶点A、C重合，求折痕EF的长。

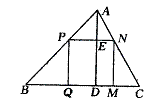4、△ABC是一块余料，边BC=120mm，高AD=80mm，要把它加工成正方形，使一边在BC上，其余两个顶点分别在AB、AC上，这个正方形零件的边长是多少？

5、李老师购买一套单元楼房，房价10万元，与房产公司签订如下付款合同：首期付4万元，其余6万元在银行办理住房袋款，月息0.4%，120个月还清，从贷款之日起，每月28日向银行还本金500元和当月的利息，贷款期限为2000年1月1日起到2009年12月30日止。第一个月向银行还本息和500+60000×0.4%，第二个月还本息和500+（60000 – 500）×0.4%，设第x月的本息和为y元。

（1）求贷款月数x和当月应还本息和y的函数关系式；

（2）今年7月28日，李老师应向银行还本息和多少元？

（3）到2009年12月30日还清贷款后，李老师共向银行还利息多少元？

6、隔湖相对的A、B两地，无法直接测量它们之间的距离，请你用所学的知识，采用两种不同的方案，得到A、B两地之间的距离，说出你具体的想法、做法及所用的知识（主要运用相似或解直角三角形的有关知识）。

7、已知反比例函数和一次函数y=2x-1，其中一次函数的图象经过（a,b），（a+1,b+k）两点。

⑴求反比例函数的解析式；

⑵如图，已知点A（m，1）在第一象限，且同时在上述两个函数图象上，求点A坐标；

⑶利用（2）的结果，请问：在x轴上是否存在点P，使△AOP为等腰三角形？若存在，把符合条件的P点坐标求出来；若不存在，请说明理由。