八年级数学期末复习（三）
第18章 图形的相似（1）
班级 姓名 得分
一、填空题（每小题2分，共20分）
1.已知△ABC与△A'B'C'中，AB=6，BC=8，A'C'=4.5，B'C'=4，要使△ABC∽△A'B'C'，则必有A'B'= .
2.地图上两地间距离为5cm，表示实际距离100km，则地图的比例尺为 .
3.三角形中两边中点的连线段与第三边之比为 .
4.如图1，两个多边形若相似，则x只能取 .
 |
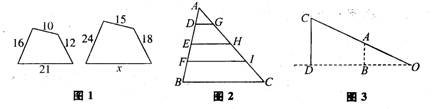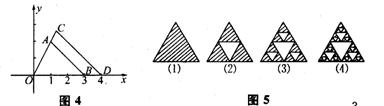
5.如图2，△ABC中，DC//EH//FI//BC，则图中相似三角形有 对.
6.两个相似三角形的边长之比为m，面积之比为5，则
= .
7.某人身高1.7米，某一时刻影长2.04米，同时一棵树影长为10.2米，则此树高 米.
8.如图3，小李在打网球时，使球恰好能打过网，而且落在离网6米的位置（BO长），若小李击球的高度2米（CD），网高0.8米，则击球处离网距离 米.
9.如图4，△AOB以O位似中心，扩大到△COD，各点坐标分别为：A（1，2）、B（3，0）、D（4，0）则点C坐标为 .
10.观察图5，若第一个图中阴影部分面积为1，第二个图中阴影部分面积为4/3，第三个图中阴影部分面积为16/9，第四图中阴影部分的面积为64/27，则第n个图中阴影部分面积为 .
二、选择题（每小题2分，共20分）
11.下列说法：①所有的直角三角形都相似；②所有的等腰三角形都相似；③所有的正方形都相似；④所有的菱形都相似，正确的有 （ ）
A、2个 B、3个 C、4个 D、1个
12.在△ABC与△A'B'C'中，∠B=∠B'=Rt∠，∠A=30°，则以下条件，不能保证△ABC与△A'B'C'相似的为 （ ）
A、∠A'=30° B、∠C'=60° C、∠C=60° D、∠A'=2/1∠C'
13.如图6、线段AB上有三点C、D、E，AB=8，AD=7，CD=4，AE=1，则比值不为1/2的线段比为 （ ）
A、AE：EC B、EC：CD
C、CD：AB D、CE：CB
14.要使正方形ABCD和菱形EFGH相似，则增加的条件不正确的是 （ ）
A、∠G=60° B、EH⊥HG C、∠E=∠F D、 ∠G+∠E=180°
15.△ABC中，DE//BC，交AB、AC于D、E，AD=6，AE=4，BD=5，则EC长为 （ ）
A、3/10 B、3 C、3/22 D、2/7
16.如图7，已知AD是△ABC的中线，AE=EF=FC，下面给出三个关系式：
AG：AD=1:2； ②GE：BE=1:3 ③GE：BE=4:3，其中正确的为 （ ）
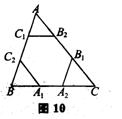
A、① ②
B 、① ③ C、 ② ③ D、①②③
图9
17.如图8，△ABC，AB=12，AC=15，D为AB上一点，且AD=
AB，在AC上取一点E，使以A、D、E为顶点的三角形与 ABC相似，则AE等于
（ ）
A、
B、10
C、或10 D、以上答案都不对
18.如图9，1ABCD中，CE交BD、AB于G、F，则图中的相似三角形有 （ ）
A、4对 B、5对 C、6对 D、7对
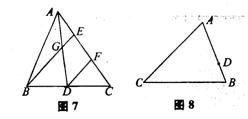
19.如图10，点A1，A2，B1、B1，B2，C1，C2是△ABC的三边的三等分点，△ABC 的周长为L，则六边形A1A2B1B1B2C1C2的周长为 （ ）
A、
L B、
L C、2L
D、
L
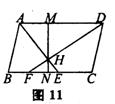20.如图11，1ABCD中，E为BC中点，F为BE中点，AE、DF交于H，过H的直线垂直于AD，交于AD、BC于M、N，则NH：MH的值为（ ）
A、2/1
B、3/1
C、4/1 D、5/1
三、解答题（60分）
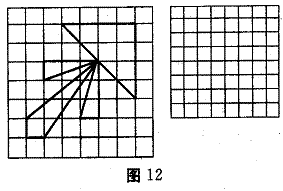21. （4分）在图12的网络中，描述右边图形的缩小图.
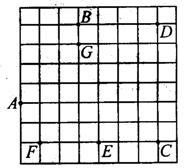22. （5分）图13是小于所在学校的平面示意图，其中各点分别表示：A（大门）；B（教学楼）；C、（宿舍）；D、（食堂）；E（操场）；F（卫生室）；G（国旗），请你选择适当的坐标系，使所标的点尽量多的在坐标轴上.
（1）根据坐标系描述食堂、宿舍、教学楼的位置；
（2）其它各点中，哪一点距卫生室（F）最近？
（3）现确定一图书馆的准确位置：使得与B、D、C三点的距离都相等，请标出此出，并说明理由.
图13
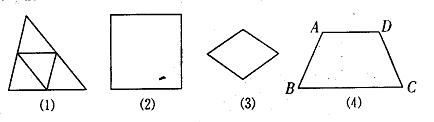
23. (7分)已知，连结三角形三边中点，把任意三角形分成四个小三角形，它们的形状，大小完全相同，并且与原三角形相似，如图（1）请把图（2）、（3）、（4）同样分成四块，使它们形状大小相同，且都和原图形相似，（注：图（2）为正方形，图（3）为菱形，图（4）为等腰三角形，且AD//BC，AB=CD=AD，∠B=60°）
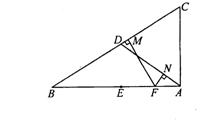
24.（8分）如图，D为Rt△ABC的斜边BC中点，E为AB的中点，F为AE的中点，FM⊥BC,FN⊥AD,垂足分别为M、N，试确定FM是FN的几倍，并说明你写结论的正确性.
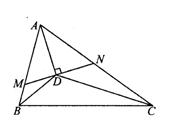
25. （8分）如图，△ABC中，三条内角平分线交于D，过D作AD垂线，分别交AB、AC于M、N，请写出图中相似的三角形，并说明其中两对相似的正确性.
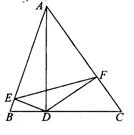26.（8分）如图，AD为△ABC的高，DE⊥AB，DF⊥AC，垂足分别为E、F，试判断∠ADF与∠AEF的大小，并说明明理由.
27.（10分）如图，在△ABC中，点D、E分别在BC、AB上，且∠CAD=∠ADE=∠B，
AC：AD：DC=2：2：1， BD：BC=5：3，设△EBD、△ADC、△ABC的周长分别为m1、m2、m3，求m1：m2：m3.
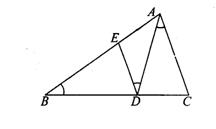
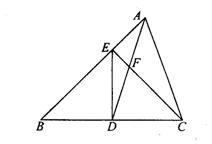28.（10分）如图，已知△ABC中，D为BC中点，AD=AC，DE⊥BC，DE与AB交于E，EC与AD相交于点F.
（1）△ABC与△FCD相似吗？请说明理由；
（2）若S△ABC=5，BD=10，求DE的长.