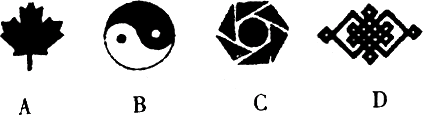八年级数学（上）综合测试题

一、填空题

1、的平方根为__________，的立方根为__________.

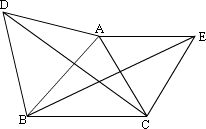
2、如图，△ABD和△ACE都是等边三角形，则△__________和△__________绕点__________旋转得到的。

3、若 □ABCD的周长为22cm，对角线AC、BD相交于O，△AOD的周长比△AOB的周长小3cm，则AD=__________cm，AB=__________cm.

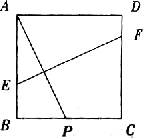
4、如图，在正方形ABCD中，AP=13cm，点A和点P是关于EF为轴的对称点，则EF的长为__________cm.

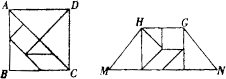
5、七巧板是我们祖先创造的一种智力玩具，它来源于勾股法。如图（1），整幅七巧板是由正方形ABCD分割成七小块（其中：五块等腰直角三角形、一块正方形和一块平行四边形）组成。如图（2）是由七巧板拼成的一个梯形，若正方形ABCD的边长为12cm，则梯形MNGH的周长是___________cm。（结果保留根号）（2002年福建宁德）

6、已知点A（－8，6），它到x轴的距离是___________，它到y轴的距离是___________，它到原点的距离是___________。

7、长沙向北京打长途电话，设通话时间为x（分），需付电话费y（元），通话3分钟以内话费为3.6元，请您根据图中y随x变化的图象找出通话5分钟，需付话费为___________.

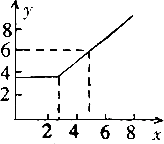
8、如果一次函数y=kx＋b的图象经过点（3，0），且与坐标轴围成的三角形的面积为6，则这个一次函数解析式为___________。

9、二次一次方程组的解为___________，且其解为直线___________和直线___________的交点坐标.

10、某射击选手在10次射击中的成绩如下表：

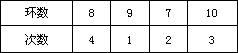
这组数据的平均数是 ___________，中位数是___________，众数是___________.

二、选择题

11、下列各组数据中，能构成直角三角形的是（ ）

A．13，16，19　　　 B．17，21，23

C．18，24，36　　　 D．12，35，37

12、已知等腰直角三角形的直角边长为3，则其斜边长为（ ）

A．整数　　　　　　 B．有限小数

C．有理数　　　　　 D．无理数

13、若数轴上表示数a的点在原点左边，则化简的结果是（ ）

A．3a　　　　　　　 B．－3a

C．a　　　　　　　　D．－a

14、将两个全等三角形用各种不同的方法拼成四边形，在这些拼成的四边形中，平行四边形的个数是（ ）

A．1个　　　　　　　B．2个

C．3个　　　　　　　D．4个

15、下列图案既是中心对称，又是轴对称的是（ ）

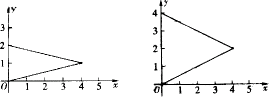
16、如图中两图形的变化是（ ）

A．平移　　　　　　 B．轴对称

C．扩大　　　　　　 D．拉伸

17、如果一次函数y=kx＋b的图象不经过第二象限，则k、b应满足（ ）

A．k>0，b<0　　　　 B．k>0，b≤0

C．k<0，b>0　　　　 D．k<0，b≤0

18、代数式x2＋ax＋b中，当x=2时，其值为3，当x=－3时，其值是4，则代数式a－b的值是（ ）

A．－1　　　　　　B．－3

C．8　　　　　　　D．3

19、某班学生查视力，结果如下：

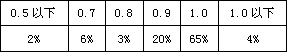
那么全班视力数据的众数如下（ ）

A．65%　　　　　　　B．20%

C．1.0　　　　　　　D．0.9

20、直线y=x＋3与x轴、y轴分别交于点A，B；直线y=2x＋1与x轴、y轴分别交于D、C两点，则四边形ABCD的面积为（ ）

A．8.5　　　　　　　B．4.75

C．4.25　　　　　　 D．9.5

三、解答题

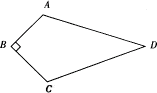
21、已知，如图，四边形ABCD中，∠B=90°，AB=3，BC=4，CD=12，AD=13，求四边形ABCD的面积.

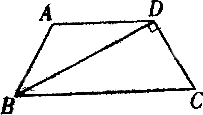
22、如图在梯形ABCD中，AD∥BC，AB=DC，BD⊥DC，且BD平分∠ABC，若梯形的周长为20cm，求此梯形的中位线长.（2002年湖北黄冈）

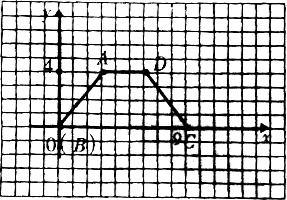
23、如图，梯形ABCD，腰AB=CD=5，点A到x轴的距离是4，点C的坐标为（9，0），求点D的坐标.

24、（2002年陕西）已知直线y=2x＋1.

（1）求已知直线与y轴交点A的坐标；

（2）若直线y=kx＋b与已知直线关于y轴对称，求k与b.

25、（2000年，江苏扬州）某中学组织初一学生春游，原计划租用45座客车若干辆，但有15人没有座位；若租用同样数量的60座客车，则多出一辆车，且其余客车恰好坐满。已知45座客车每日租金每辆220元，60座客车日租金为每辆300元，试问：

（1）初一年级人数是多少？原计划租用45座客车多少辆？

（2）若租用同一种车，要使每位同学都有座位，怎样租用更合算？

26、《中华人民共和国个人所得税》规定，公民用工资，薪金所得不超过800元的部分不必纳税，超过800元的部分为全月应纳税所得额。此项税款按下表累计计算：

（纳税款 =应纳税所得额×对应的税率）

按此规定解答下列问题：

（1）设某甲的月工资、薪金所得为x元（1300<x<2800），需缴交的所得税款为y元，试写出y与x的函数关系式；

（2）若某乙一月份应缴交所得税款95元，那么他一月份的工资、薪金是多少元？

答案：一、1 、∵，∴ 2 的平方根为 ±，立方根为

2 、∵ AD=AB ， AE=AC ，∠DAC= ∠BAE.

　　∴ △ACD 和△AEB 绕点 A 旋转得。

3 、∵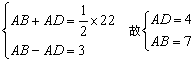

4 、 EF=13cm

　　提示：过 B 点作 BG ∥ EF 交 DC 于 G ，则 BG=EF ，又△BGC ≌△APB ，

　　　　　∴ BG=AP=13 ，∴ EF=13.

5 、（24＋ 24） cm

　　提示：∵ MH＋NG=AD＋DC=24.

　　　　　.

　　　　　故梯形周长为（24＋ 24） cm.

6 、 6 ， 8 ， 10

7 、 6 元

8 、 y=－x＋4 或 y=x－4

　　提示：设 y=kx＋b 交 y 轴于（0 ， b），有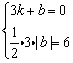

　　　　　∴

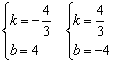
　　　　　∴ y=－x＋4 或 y=x－4

9 、

10 、 8.5 ， 8 ， 8

二、答案：

　　11 、 D 12 、 D 13 、 D 14 、 C 15 、 D

　　16 、 D 17 、 B 18 、 D 19 、 A 20 、 C

提示：

　　11 、 12²＋35²=37².

　　12 、斜边长为 3是无理数 .

　　13 、∵ a<0 ，∴ 原式 =2a－a=a=－a.

　　17 、

　　　　∵ 不经过第二象限，∴ k>0 ， b ≤ 0.

　　18 、

　　　　有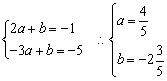

　　　　则.

　　20 、先画图象，后求面积 .

三、21、提示：连 AC ，则.

△ACD 中，有 AC²＋CD²=5²＋12²=16⁹=AD²

∴ ∠ACD=90 °

故

22、中位线长为 6cm.

提示：可证 AD=AB=DC=BC.

故 5AD=20 ，∴ AD=4 ， BC=8.

∴ 中位线长为(AD＋BC)=6(cm).

23、D （6 ， 4）

提示： AB=5 ， A 到 x 轴距离是 4 ，故 A 到 y 轴距离为 3.

∴ A （3 ， 4），又 C （9 ， 0） .

∴ D 到 y 轴距离为 9－3=6.

故 D （6 ， 4） .

24、（1） A （0 ， 1）

（2） k=－2 ， b=1.

提示：∵ y=2x＋1 交 x 轴于点（－， 0） .

则该直线关于 y 轴对称的直线交 x 轴于（， 0），

故所求直线必过 A （0 ， 1）和（， 0）两点 .

有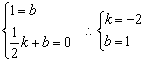

25、解：（1）设初一人数为 x ，原计划租用 y 辆 45 座客车，根据题意，得：

解得

　　（2）租用 6 辆 45 座客车的租金为： 6×220=1320 （元）

租用 4 辆 60 座客车的租金为： 4×300=1200 （元）

∴ 租用 60 座客车更合算些。

26、（1）∵ 1300<x<2800 ，∴ 500<x－800<2000.

∴ y=(x－800－500)×10%＋500×5%.

（2）∵ 500×5%<95<2000×10%＋500×5% ，

∴ 某乙工资适用（1）中的函数关系 .

∴ 95=(x－1300)×0.1＋25.

解得： x=2000.

答：他一月份工资、薪金是 2000 元 .