八年级数学第二学期调研考试试题
| 题号 | 一 | 二 | 三 | 总分 | ||||||
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | ||||
| 得分 | ||||||||||
考生注意：全卷共27道题，满分100分，考试时间120分钟.
一、选择题（每题给出的四个选项中，有且只有一个是正确的，请将正确选项前的字母填入下表相应的空格内.每题2分，计24分.）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
1、
的平方根是
A．
B．
C．
D．
2、
函数
中自变量
的取值范围是
A．
B．
C．
D．
3、
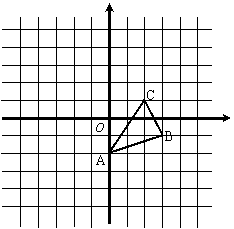
在直角坐标系内，点
关于原点的对称点的坐标是
A．
B．
C．
D．
4、 下列图形中一定相似的是
A. 两个等腰三角形 B.两个直角三角形
C.两个矩形 D.两个正方形
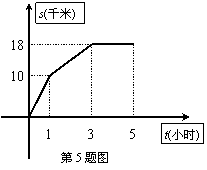
5、 某人骑车外出，所行路程s（千米）与时间t（小时）的函数关系如图所示，现有以下四种说法：①最初的1小时骑车的速度最快；
②最初的1小时骑车的速度最慢；③出发后4小时距离起点18千米；④一直骑了5小时，没有休息；其中说法正确的是
A．①③ B．②④ C．①④ D．②③
6、
如图，反比例函数的图象经过点
，则其函数解析式为
A. 
B. 
C. 
D. 
7、△ABC的三边长分别为6、8、10，与△ABC相似的△
的最短边的长为2，则△的周长是
A.
B.
C.
D.
8、在数轴上，实数
对应的点分别为A、B，点A关于B的对称点为C，则点C表示的数是
A．
B．
C．
D．
9、化简
的结果是
A．
B．
C．
D．
10、如图，在所示的直角坐标系中，P
是第一象限内的点，OP与轴的正半轴的夹角为
，且
，则
的值为
A.
B.
C.
D.
11、已知甲、乙两班的人数均在40至50之间，根据给出的统计图（见上图），比较甲、乙两班的团员人数，则
A.甲班少 B.乙班少 C.一样多 D.无法比较确定
12、从放有三个红球、两个白球、一个黄球的袋中，随意摸出两个球，发生机会最小的事件是
A.都是红球 B.一个红球，一个白球 C.都是白球 D.一个白球，一个黄球
二、填空题（每题3分，计24分）
13、
的立方根是______________.
14、
15、已知点
都在直线
上，则
_____
.（填＜、＞或＝号）
16、一组数据共8个数：
.则这组数据的标准差为___________.
17、如图是函数
的图象，则不等式
的解集是____________.
18、如图，已知∠1＝∠2，若再增加一个条件就能使△ABC∽△ADE，这个条件可以是________________________.
19、抛两枚普通硬币，则“至少有一枚硬币是反面”这一事件发生的机会是______.
20、如图是一堤坝的断面图，上底AD＝6米，堤坝的高为10米，坡面AB与地面的倾角为
，斜坡CD的坡度
，则堤坝的底BC的长为________米.
三、解答题（共6道题，计52分）
21、（本题6分）
计算：
22、 （本题6分）
按要求解答下列问题：
(1)
如图，以点O为位似中心，画出△ABC的位似图形△，使得△与△ABC的相似比为2：1；
(2)
求△的面积.
23、（本题6分）
已知一次函数
的图象与反比例函数
的图象相交，其中一个交点的横坐标为3.
（1）
求
的值；
（2）
求直线被两坐标轴截得的线段的长.
24、（本题8分）
如图(1)，为了求河的宽度，在河对岸岸边任意取一点A，再在河这边沿河边取两点B、C，使得∠ABC＝
，∠ACB＝，量得BC的长为30米.
（1）
求河的宽度；（参考数据：
，精确到
米）
（2）
请你再设计一种测量河的宽度的方案，在下面的图(2)中画出示意图，并对你的方案作简要的文字说明.
25、（本题8分）
为调查某地区居民的生活水平，有关部门在该地区随机抽取了50户，对这50户家庭的存款额进行了调查，数据（单位：万元）如下：
1.6 3.5 2.3 6.5 2.2 1.9 6.8 4.8 5.0 4.7
2.3 1.5 3.1 5.6 3.7 2.2 3.3 5.8 4.3 3.6
3.8 3.0 5.1 7.0 3.1 2.9 4.4 5.8 3.8 3.7
3.3 5.2 4.1 4.2 4.8 3.0 4.0 4.6 6.0 2.4
3.3 6.1 5.0 4.9 3.0 3.1 7.2 1.8 5.0 1.9
根据以上数据，解答以下问题：
| 存款额 | 频数记录 | 频数 |
| 1.0≤ | 正 | |
| 2.0≤ | ||
| 3.0≤ | ||
| 4.0≤ | ||
| 5.0≤ | ||
| 6.0≤ | ||
| 7.0≤ |
（1） 求这50户家庭的存款额的极差是多少？
（2） 将这50户家庭的存款额分成7组，试完成右边的表格；并制作频数分布直方图；
（3）
按存款额1.0≤＜3.0；3.0≤＜6.0；6.0≤＜8.0分成温饱、小康、较富裕三种类型，试画出这三种类型的扇形统计图；
（4） 若该地区共有10000户居民，试估计达到小康的约有多少户？
26、（本题8分）
如图，在
ABCD中，过点B作BE⊥CD，E为垂足，连结AE，
F为AE上的一点，且∠BFE＝∠C.
（1） 试说明：△ABF∽△EAD；
（2）
若AB＝4，∠BAE＝
，求AE的长；
（3） 在(1)、（2）的条件下，若AD＝3，求BF的长.（计算结果保留根号）
27、（本题10分）
如图，锐角△ABC的一边BC＝120，BC边上的高AD＝80，矩形EFGH的一边在线段BC上，另两个顶点分别在边AB、AC上.
(1)
设
,求
与之间的函数关系式；
(2)
记矩形EFGH的周长与△ABC周长的比为，问是否可能等于
？试说明理由；
(3)
题（2）中的比值是否可能等于？为什么？
.