八年级（下）相似三角形练习卷
一、填空题
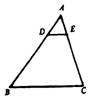
1．如图1，D,E分别是△ABC的边AC,AB上的点，当△AED和△ACB满足条件 时，使得△AED～△ACB.（填上你认为正确的一种条件即可，不必考虑所有可能的情形）
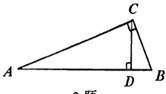
2．如图2，在ΔABC中，∠ACB=90°，CD⊥AB，垂足为D，AC=12，BC=5，则CD的长是
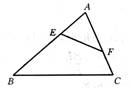
3．如图3，要使△ＡＥＦ∽△ＡＣＢ，已具备条件 还需补充的条件是 ，或 ，或
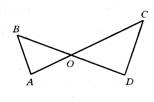
4．如图，线段ＡＣ、ＢＤ相交于点Ｏ，要使△ＡＯＢ∽△ＤＯＣ，已具备条件 还需补充的条件是 或 或
（第1题） （第2题） （第3题） （第4题）
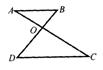
5．如图5，AB∥DC，AC交BD于点O．已知
，BO＝6，则DO=_________。
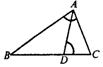
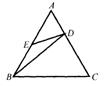
6．如图6，在△ABC中，点D在线段BC上，∠BAC=∠ADC，AC=8，BC=16，那么CD=__________。
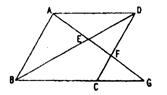
7．如图7，平行四边形ABCD中，G是BC延长线上一点，AG与BD交于点E，与DC交于点F，
则图中相似三角形有
8．如图8，已知△ADE∽△ABC，相似比为2：3，则
=（ ）
（A）3：2 （B）2：3 （C） 2：1 （D）不能确定
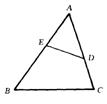
9．如图9，在正三角形ABC中，D、E分别在AC、AB上，且AD：AC=1：3，AE=BE，则有（ ）
△AED∽△BED （B）△AED∽△CBD
（C）△AED∽△ABD （D）△BAD∽△BCD
（第5题） （第6题） （第7题） （第8题） （第9题）
二、解答题
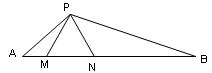
1．已知：如图，△PMN是等边三角形，∠APB=120°。 求证：AM·PB = PN·AP。
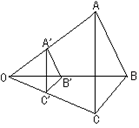2.已知，如图，AB∥A'B'，BC∥B'C' 求证：△A'B'C'∽△ABC
3.▱ABCD中E是对角线AC上任一点，过E的直线，PS分别交AB的延长线，BC、AC、AD、CD的延长线
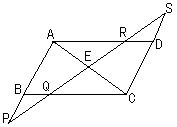于P、Q、E、R、S。求证：EP·EQ=ER·ES
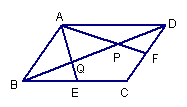
4.：▱ABCD中，E为BC中点，F为CD中点，AE、AF分别交BD于P、Q，求证：BP=PQ=QD
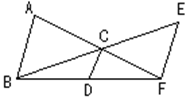5.如图，AB∥CD∥EF求证：
 |
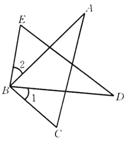6.如图，∠１＝∠２，∠Ｄ＝∠Ａ．求证△ＡＢＣ∽△ＤＢＥ．
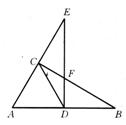7.已知：如图，ＣＤ是Ｒｔ△ＡＢＣ斜边上的中线，过点Ｄ垂直于ＡＢ的直线交ＢＣ于点Ｆ，
交ＡＣ的延长线于点Ｅ．
求证：（１）△ＡＤＥ∽△ＦＤＢ；（２）