八年级
 第二学期期中数学试题1
第二学期期中数学试题1
一、想一想、填一填(每题3分,共24分)
 1.不等式组2≤3x-7<8的整数解为_________;
1.不等式组2≤3x-7<8的整数解为_________;
2. 若分式方程![]() 有增根,则m的值是____。
有增根,则m的值是____。
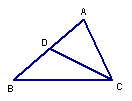
3.如图,D是△ABC的AB边上一点,要使△
ABC∽△ACD则还须具备一个条件是________.(只填一个符合要求的条件即可)
4.如图,测量小玻璃管口径的量具ABC,AB
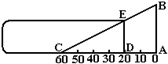 的长为10cm,AC被分为60等份.如果小玻璃管口DE正好对着量具上20等份处(DE∥AB),那么小玻璃管口径DE是_________cm。
的长为10cm,AC被分为60等份.如果小玻璃管口DE正好对着量具上20等份处(DE∥AB),那么小玻璃管口径DE是_________cm。
5. 对于整数![]() ,b,c,d,符号
,b,c,d,符号![]() 表示运算
表示运算![]() ,已知1<
,已知1<![]() <3,则b+d的值是_________.
<3,则b+d的值是_________.
6. 请举一个发生的概率是![]() 的事件:__________________________.
的事件:__________________________.
7. 若双曲线y=![]() 的图象在第一、三象限,那么m的值为____________
的图象在第一、三象限,那么m的值为____________
8.把命题“等角的补角相等”写成“如果…,那么…”的形式________________________.。
二、看一看、选一选(每题3分,共36分)
9.设“○”、“□”、“△”分别表示三种不同的物体,用天平比较它们质量的大小,两次情况如图所示,那么每个“○”、“□”、“△”这样的物体,按质量从小到大的顺序排列为( )
A.○□△ B.○△□ C.□○△ D.△□○
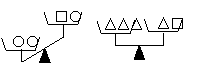 10. 把分式
10. 把分式![]() 中的a、b都扩大2倍,则分式的值( )
中的a、b都扩大2倍,则分式的值( )
A. 扩大4倍 B. 扩大2倍 C. 缩小2倍 D. 不变
11. 若分式![]() =0,则x
的值为( )A 4 B -4 C ±4 D ±2
=0,则x
的值为( )A 4 B -4 C ±4 D ±2
|
|
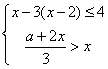 无解,则a的取值范围是( )
无解,则a的取值范围是( )
 A.a<1 B.a≤1 C.a>1
D.a≥1
A.a<1 B.a≤1 C.a>1
D.a≥1
|
|
|
|
A 3对 B 4对 C 5对 D 6对
14.某天同时同地,甲同学测得1m的测竿在地面上影长为0.8m,乙同学测得国旗旗杆在地面上的影长为9.6m,则国旗旗杆的长为( )(A)10m(B)12m(C)13m(D)15m
15.在同一坐标系中画函数y=![]() 和y=-kx+3的图象,大致图形可能是
和y=-kx+3的图象,大致图形可能是
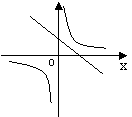 | |||||||
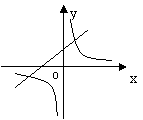 | 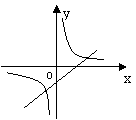 | 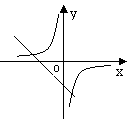 | |||||
A B C D
16. 一个钢筋三角架,长分别为20cm 、50cm、60cm,现要再做一个与其相似的钢筋三角架,而只有长为30cm和50cm的两根钢筋,要求以其中的一根为一边,从加一根截取下两段(允许余料)作为另两边,则不同的截法有
A、1种 B、2种 C、3种 D、4种
17. 中央电视台“幸运52”栏目的“百宝箱”互动环节,是一种竞猜游戏。游戏规则如下:有5个商标牌的背面注明了一定的奖金额。其余商标牌的背面是一张哭脸,若翻到哭脸就不得奖,参与这个游戏的观众有三次翻牌的机会。某观众前两次翻牌均获得若干奖金,如果翻过的牌不能再翻,那么这位观众第三次翻牌获奖的概率是( )
 A.
A.![]() B。
B。![]() C。
C。![]() D。
D。![]()
18、如图,点P是x轴上的一个动点,过点P作x轴的垂线PQ
交双曲线于点Q,连结OQ, 当点P沿x轴正半方向运动时,
Rt△QOP面积 ( )
A.逐渐增大 B.逐渐减小 C.保持不变 D.无法确定
19. 有一对酷爱运动的年轻夫妇给他们12个月大的婴儿拼排3块分别写有“20”,“08”,和“北京”的字块,如果婴儿能够排成“2008北京”或者“北京2008”,则他们就给婴儿奖励,假设婴儿能将字块横着正排,那么这个婴儿能得到奖励的概率是( )
A.![]() B。
B。![]() C。
C。![]() D。
D。![]()
20. 若点(-![]() ,
,![]() )(3,
)(3,![]() )(8,
)(8,![]() )都在反比例函数
)都在反比例函数![]() 的图象上,则下列各式正确的是( )
的图象上,则下列各式正确的是( )
A、![]() <
<![]() <
<![]() B、
B、![]() <
<![]() <
<![]() C、
C、![]() <
<![]() <
<![]() D、
D、![]() <
<![]() <
<![]()
三、解一解、求一求,用一用(12分+8分+8分+10分+10分+12分)
21.解下列不等式(组),并把解集表示在数轴上
(1)、![]() (2)、解不等式组
(2)、解不等式组 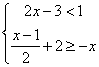
22.有这样一道试题:“计算:![]() 的值,其中
的值,其中![]() .”甲同学把“
.”甲同学把“![]() ”错抄成“
”错抄成“![]() ” ,但他的计算结果也是正确的.你说这是怎么回事?
” ,但他的计算结果也是正确的.你说这是怎么回事?
23.四张大小,质地均相同的卡片上分别标有数字1,2,3,4,现将标有数字的一面朝下扣在桌子上,从中随机抽取一张(不放回),再从桌子上剩下的3张中随机抽取第二张。
(1)用画树状图的方法,列出前后两次抽得的卡片上所标数字的所有可能情况
(2)计算抽得的两张卡片上的数字之积为奇数的概率?
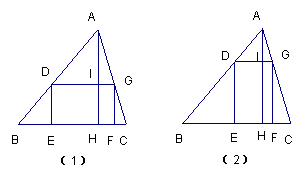 24.有一块三角形铁片ABC,BC=12cm,高AH=8cm,按图(1)(2)两种方法设计,把它加工成一块矩形铁片DEFG,使矩形的长是宽的2倍,试分别求出按(1)(2)两种设计加工成的矩形铁片的面积,并比较两种设计方法的优劣.
24.有一块三角形铁片ABC,BC=12cm,高AH=8cm,按图(1)(2)两种方法设计,把它加工成一块矩形铁片DEFG,使矩形的长是宽的2倍,试分别求出按(1)(2)两种设计加工成的矩形铁片的面积,并比较两种设计方法的优劣.
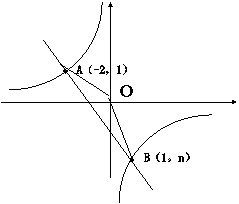
24..如图,一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像相交于A、B两点,
的图像相交于A、B两点,
(1)利用图中条件,求反比例函数和一次函数的解析式
(2)求![]() 的面积
的面积
(3)根据图像写出使一次函数的值大于反比例函数的值的![]() 的取值范围;
的取值范围;
 |
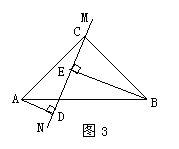
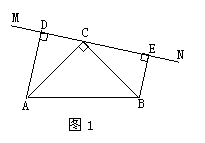
10、在△ABC中∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)当直线MN绕点C旋转到图1的位置时,求证:
①△ADC≌△CEB;②DE=AD+BE;
(2)当直线MN绕点C旋转到图2的位置时,求证:DE=AD-BE;
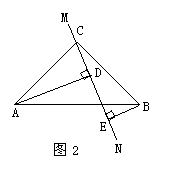 (3)当直线MN绕点C旋转到图3的位置时,试问DE、AD、BE具有怎样的等量关系?请写出这个等量关系,并加以证明.
(3)当直线MN绕点C旋转到图3的位置时,试问DE、AD、BE具有怎样的等量关系?请写出这个等量关系,并加以证明.
 | |||
 | |||