八年级第二学期数学期末试卷
(A卷，共计100分)
一、 填空题（每小题3分，共36分）
1若点A（m,2）与点B（3,n）关于原点对称，则m,n 的值分别是（ ）
Ａ －３，２ Ｂ ３，－２ Ｃ －３，－２ Ｄ ３，２
２、△ABC中 ,若各边长都扩大２倍。则锐角Ａ的的三角函数值（ ）
Ａ 都扩大３倍 Ｂ 都缩小３倍 Ｃ 无变化 Ｄ 都扩大９倍
３、函数y=
中自变量x的取值范围是（ ）
Ａ x>2 且x≠1 Ｂ x>2 Ｃ x≥－２且x≠1 Ｄ x≤2且x≠－１
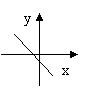
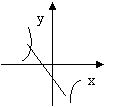
4、一次函数y=kx+b的图象如图所示，则正确的是（ ）
Ａ k>0, b>0 Ｂ k>0 ,b<0
Ｃ k<0, b>0 Ｄ k<0, b<0
5 、△ABC中，Ｄ，Ｅ分别在AB，AC上，且DE∥BC,AD＝3,BD=4, 则DE：BC=（ ）
Ａ 7/3 Ｂ 3/7 Ｃ 4/3 Ｄ 3/4
6、样本101，102，98，99的标准差是（ ）
A 
B 0 C 1 D 
7、下列说法①两个直角三角形是相似三角形，②两个全等三角形是相似三角形，③锐角三角形都是相似三角形，④等边三角形是相似三角形，⑤两个等腰直角三角形是相似三角形。其中正确的有（ ）个
A 1 B 2 C 3 D 4
8、函数y=kx－k与y=k/x在同一坐标系中的图象大致是（ ）
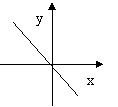
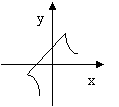
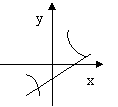
A
B
C
D
 | |||
 | |||
９、两个相似三角形的周长分别是８和６，则它们的相似比为（ ）
Ａ ４：3 Ｂ 2：3 Ｃ 16：9 Ｄ 3：2
10、当锐角A>30０时,CosA的值( )
A <1/2 B >1/2 C >
D
<
11、某水库大坝的横截面是梯形，两面的坡度分别为1：3和1：1，则这两个坡角的和是（ ）度。
A 90 B 75 C 60 D 105
12、若x1,x2,x3,x4,x5的平均数是2，方差是0.5，则2x1,2x2,2x3,2x4,2x5的平均数和方差分别是（ ）
A 4，1 B 1，4 C 4，2 D 2，4
二、 填空题（每空３分，共３０分）
13、若x/2=y/3=z/4 ,则x+y+z/2x= 。
14、一根电线杆在地面影长为40米，同时，高为1.2 米的测杆在地面上的影长为2米，则电线杆的高度是 。
15、从装有同样大小的2个黄球、4个红球的口袋中，任意摸出一个球恰为红球的机会是 。
16一船向正东方向航行，上午8：00在B处，看到一灯塔在它的北偏东600、距离为72海里的A处，上午10：00到达C处，此时灯塔在它的正北方，则此船的航行速度为 。
17、已知y与x成反比例，且当x=2时y= －１，则当y=1/2时，x= 。
18、计算
+
+
－
=
。
19、已知正方形ABCD的边长为2，现以对角线所在的直线为坐标轴，则四个顶点的坐标分别是 。
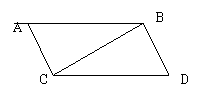20、如图，已知∠ACB=∠CBD=900，AC=b，BC=a，若△ABC∽△CBD，写出 BD与a、b之间满足的关系式 。
21、计算tan300cot450+Sin600－1/2Cos450=
。
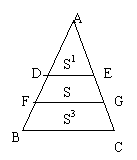
22、如图，△ABC被DE、FG分成面积相等的三部分，（S1=S=S3）
且DE∥FG∥BC，则DE：FG：BC= 。
三、 解答题（5+7+7+7+8）
23、已知△ABC中∠C=900,a=2,∠B=600,解这个直角三角形。
24、已知一次函数y=kx+b的图象经过A（－３，－２）；B（１，６）两点。
（1） 求解析式
（2） 求此函数图象与两坐标轴围成的三角形的面积
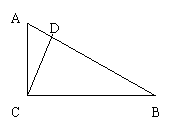25、已知如图，CD为Rt△ABC斜边AB上的高，求证AC2=AD×AB
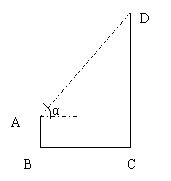26、已知如图，AB=1.5m,BC=30m,∠α=600,求CD的高。
27、已知如图，平行四边形ABCD中AE：EB=1：2
（1）
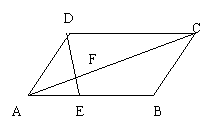求△AEF与△CDF的周长比。
（2）若S△AEF=6cm2求S△CDF
（B卷，共计50分）
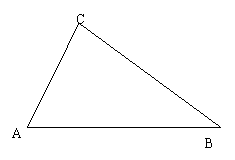28、如图，△ABC中，∠A=600，∠B=450，AB=60，求AB边上的高。（12分）
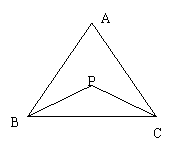29、如图，△ABC中，∠B与∠C的平分线交于点P，设∠A=x、∠BPC=y，当∠A变化时，求y与x之间的函数关系式。并判断y 是不是x的一次函数，说明x的取值范围。（15分）
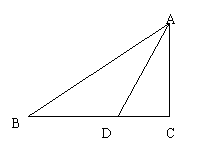30、如图△ABC中∠C=900，∠B=300，AB=2，且AC=BD，求cot∠ADC的值。（12分）
31、已知等腰三角形两边长分别为2和4，求这个等腰三角形底角的四个三角函数值以及此三角形的面积。（11分）