八年级上期末数学监测
数 学
（全卷共三个大题，28个小题，满分100分，考试时间90分钟）
| 题号 | 一 | 二 | 三 | 总分 | 总分人 |
| 得分 |
| 得分 | 评卷人 |
一、填空题：（本大题共10个小题，每小题2分，共20分）请将正确
答案直接填写在题中的横线上。
1．
1－
的绝对值＝___________； 
＝______________；
2． 如图，有一个长方体盒子，长70厘米，宽和高都是50厘米， 50
在A处有一只蚂蚁想吃到B处的食物。若蚂蚁爬行的速度
为1.3厘米每秒，它最少需要爬行__________秒才能吃到食物。Ａ ７０
3．
一个多边形的内角和等于5400，那么这人多边形为_________边形；
y
4． 如图，矩形ABCD中，点A（-4，1）、B（0，1）、C（0，3），则 D C
点A 到x轴的距离是____________，点A关于x轴的对称点
A’坐标是____________；点D坐标是（ ），点D到 A B
原点的距离是______________； O x
5．
一次函数y=kx＋b 的图象过点A（-1，2），且与y轴交于点B， OAB的面积是2，
则这个一次函数的表达式为 。
6． 若直线y=x＋3和直线y=－ｘ＋ｂ的交点坐标为（m，8），则m= ，b= 。
7．
直角三角形有两边长分别为3，4，则该直角三角形第三边为 。E C
8．
如图，Rt ABC中，AB=1cm，AC=2cm，将 ABC绕点A按逆时针
|
方向旋转260得到 ADE，则DE= cm， BAD= 。
9．
已知
是方程2x－ay=5的一个解，则a= 。
A
B
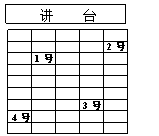
10． 教室中有9排5列座位，请根据下面四个同学的描述，
在右图中标出“5号”小明的位置，1号说：“小明在我的右
后方。”2号同学说：“小明在我的左后方。”3号同学说：“小
明在我的左前方。”4号同学说：“小明离1号和3号同学的
距离一样远。
| 得分 | 评卷人 |
二、选择题：（本大题共10个小题，每小题3分，共30分）在每小题给出的四个选项中有且只有一项是符合题目要求的，请将正确选项的番号填在题后的括号内
11．2的不立根是（ ）
A B
＋ Ｃ ４ Ｄ ＋４
12．在平行四边形、矩形、菱形、正方形、等腰梯形中，对角线相等的有（ ）
A 1个 B 2个 C 3个 D 4个
13．与数轴上的点一一对应的数是（ ）
A 有理数和无理数 B 无理数 C 有理数 D 分数或整数
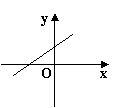
14．已知正比例函数y=kx（k＝0）的函数值y随x的增大而减小，则一次函数y=x+k
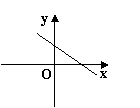
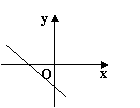
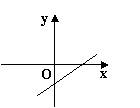的图象大致是（ ）
 |
A B C D
15．四边形ABCD的对角线AC、BD相交于点O，AD∥BC，AD=BC，使四边形ABCD
为正方形，下列条件中：①AC=BD；②AB=AD；③AB=CD；④AC⊥D。需要满
足条件（ ）
A ①② B ②③ C ②④ D ①②或①④
16．一次函数y=x图象向下平移2 个单位长度后，对应函数关系式是（ ）
A y=2x B y=x－2 C y=x D y=（1/2）x
17．若2a3xby+5与5a2-4yb2x是同类项，则（ ）
A 
B 
C 
D 
18．某青年排球队12名队员年龄情况如下：
| 年龄 | 18 | 19 | 20 | 21 | 22 |
| 人数 | 1 | 4 | 3 | 2 | 2 |
则这12名队员年龄的众数、中位数分别是（ ）
A 20，19 B 19，19 C 19，20．5 D 19，20
19．一次函数y=kx+b，经过（1，1），（2，-4），则k与b的值为（ ）
A 
B 
C 
D 
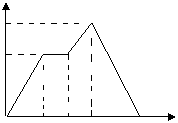
20．如图中的图象（折线ABCDE）描述了一汽车在某一直 直路上的行驶过程中，汽车离出发地的距离s（千米）和行驶时间t（小时） Y(千米)
之间的变量关系，根据图中提供的信息，给出下列 120 D
说法：①汽车共行驶了120千米；②汽车在行驶途 80 B C
中停留了0.5小时；③汽车在每个行驶过程中的平
均速度为（160/3）千米；④汽车自出发后3小时
至4.5小时之间行驶的速度在逐渐减小，其中正确 A F t(小时)
的说法共有（ ） O 1.5 2 3 4.5
A 1个 B 2个 C 3个 D 4个
| 得分 | 评卷人 |
三、 解答题：（本大题共8个小题，共50分）解答应写出文字说明或演算步骤。
21．计算下列各题：（每小题解4分，共8分）
（1）
（2）
A
22．（本题6分）如图，菱形ABCD的面积等于24，对角线BD=8。
（1） 求对角线AC的长； B D
（2） 建立适当的直角坐标，表示菱形各顶点的坐标。
C
23.(本题8分)解下列二元一次方程组（第②题用作图的方法求解）
①
②
|
| |||||||||||||||
24．（本题6分）某瓜农采用大棚栽培技术种植了一亩地的良种西瓜，这亩地产西瓜600个，
在西瓜上市前该瓜农随机摘下了10人成熟的西瓜，称重如下：
| 西瓜质量（千克） | 5.4 | 5.3 | 5.0 | 4.8 | 4.4 | 4.0 |
| 西瓜数量(个) | 1 | 2 | 3 | 2 | 1 | 1 |
（1）这10个西瓜质量的众数和中位数分别是 和 ；
（2）计算这10个西瓜的平均质量，并根据计算结果估计这亩地共可获西瓜约多少千克？
25．（本题5分）矩形ABCD的对角线相交于点O，DE//AC，CE//DB，CE、DE交于点E，请
问：四边形DOCE是什么四边形？请说明理由。 E
D C
O
A B
26．（本题5分）某同学编拟了这样一道数学命题：“如果在四边形ABCD中，AB=CD，AC=BD，
那么四边形ABCD一定是平行四边形。“若你判断这个命题结论成立，请给予证明；若
你认为这个命题的结论不一定成立，请画图举出反例予以说明。
27．（本题6分）某工厂生产某种产品，每件产品出厂价为50元，成本价为25元，因在生产过程中，平均每生产一件产品有0.5立方米污水排出,所以为了净化环境,工厂设计了两种处理污水的方案。方案一：工厂将污水先净化处理再排出，每处理1立方米污水需原料费2元，且每月排污设备损耗费为30000元；方案二：工厂将污水排到污水处理厂统一处理，每处理1立方米污水需付14元的排污费。
（1） 设工厂每日生产6000件产品，每月利润为y元，分别求出两种方案处理污水时，y与x函数关系式（利润＝总收入－总支出）；
（2） 设工厂每月生产6000件产品，则在不污染环境又节约资金的前提下，应选择哪种
方案？请通过计算加以说明。
28．（本题6分）（在下面给出的两个题中任意选作一个题解答，解答正确均可得6分）
（1）A、B两地相距50km，甲于某日下午1时骑自行车从A地出发驶往B地，乙也于同
日下午骑摩托车从A地出发驶往B地，图中折线PQR和线段MN分别表示甲和乙所
行驶的里程s与该日下午时间t之间的关系。
① 甲出发多少小时，乙才开始出发？
② 乙行驶多少小时就追上了甲，这时两人离B地还有多少千米？
（2）座钟的摆针摆动一个来回所需的时间称为一个周期，其计算公式为T=
，其中T表示周期（单位为米），g=9.8米/秒2。假如一台座钟的摆长为0.2米，它每摆动一个来回发出一次滴答声，那么在1分钟内，该座钟大约发出了多少次滴答
声？（
=3.14，结果精确到个位）
参考答案
一、1 
， —4；
2. 10； 3 五； 4 1，（-4，-1），（-4，3），5；
5 y=2x+4或y=—6x—4；
6 5，13； 7 
或5；
8 
，∠CAE ； 9 —1； 10 第5排第3列。
二、 11~15 B C A D D 16~20 B B D C B
三、 21 （1） 
（2）
22 （1）BD=8 AC=6 （2）A（0，3）B（-4，0）C（0，-3）D（4，0）
23 （1）
（2）
（图略）
24 （1） 5.0 ，5.0
（2） x =（5.4*1+5.3*2+5.0*3+4.8*2+4.4*1+4.0*1）/10 = 4.9(千克)
4.9 * 600 = 2940(千克)
25 答:四边形DOCE是菱形
26 答:不一定成立.在等腰梯形ABCD中,AB=CD,AC=BD,但它不是平行四边形.
27 解 ① 方案一利润:y1=24x – 30000
方案二利润:y2=18x
② 当x=6000时 y1=114000元 > y2=108000元 应选方案一。
28 （1） ①甲下午1时出发，乙下午2时出发，乙比甲晚出发1小时；
②乙行驶0.5小时就追上甲,此时两人离B地还有25千米
(2) 在1分钟内,该座钟大约发出了67次滴答声。