八年级上学期期末练习卷
一．耐心填一填（本题共14小题，每题2分，共28分）
1.在平面直角坐标系中P点坐标为（a,b）,当a＝0，点P在_______ 上，当b=0,点P在_______ 上.
2.若P（a,-2）与Q(3,b)关于x轴对称，则a=______, b=_______.
3.一次函数y=2x-3与x轴交点坐标为_______，与y轴交点坐标为_________.
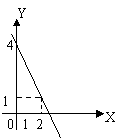
4.一次函数图象的位置如右图所示，请根据图中数据，写出一次函数的解析式__________________.
5.若
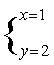是方程组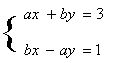
的解，则a=____, b=_______.
6.数据3，3，4，7，6，5，2，8的众数是________,平均数中________.
7.在弹性限度内，弹簧伸长的长度与拉力成正比，一根原长10cm的弹簧挂重10千
克时，其长度为15cm，则挂物重6千克时，弹簧长度的长度是_________.
8.在直角坐标系中，保持图形a的各点的横坐标不变，纵坐标乘以-1，得到图形b，则图形a,b的位置关系__________.
9.平方根等于本身的数是__________,立方根等于本身的数是_____________.
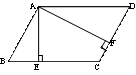
10.如图，平行四边形ABCD中，AE⊥BC,于E，AF⊥CD于F，∠ABC＝75°，则∠EAF=_________.
|
x轴上若点C在x轴上，若点C的坐标为（0，4）,则顶点A的坐标为__________.
12.如图所示，Rt△ABC中，∠ABC＝90°∠A＝32°，△ABC绕着B旋转到△A/B/C/,
此时C点恰好落在A/B/,且A/B/与A/C/相交于点D，则∠BDC=________.
13.某出租车的车费是这样计算的，路程在4km以内（包括4km）为10元，以后每增加1km加一元，达到 16km以后，每1km增加1.2元，某乘客交了21.6元车费，则庐乘客乘出租车行驶路程为________km.
14.用边长相同的正三角形、正方形、正六边形、正八边形、正十边形进行密铺，每个交叉点只允许五块进行密铺，它有_______种铺法。
二、精心选一选（本题共13小题，每题2分，共26分）
15.在－，
，－，－，0.3，
中无理数的个数是（ ）
A．1 B．2 C．3 D．4
16．的算术平方根（ ）
A．2 B．±2 C． D．±
17.甲、乙、丙、丁四种糖的售价分别为每千克12元、9元、8元、5元、若将甲种糖果7千克，乙8千克，丙5千克，丁10千克混合在一起，则这种什锦糖的售价应定为（ ）
A． 8.2元 B．7.6元 C．7.3元 D． 6.9元
18.已知（2,a）和(-3,b)在一次函数y=-x+8的图像上，则（ ）
A．a>b B．a<b C．a=b D．无法判断
19．若一次函数y=-x+㎡与y=2x+4的图象交于x轴上同一点，则m的值为（ ）
A． m=2 B．m=±2 C．m= D． m=±
20.若方程组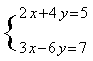
的解为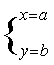
则一次函数 y=
与 y=
交点坐标（ ）
A．（b,a） B．(a,a) C．(a,b) D．(b,b)
21.某校150名学生参加数学竞赛，平均分为55分，其中及格学生平均77分，不及格学生平均47分，则不及格学生人数是（ ）
A．49 B．101 C．110 D． 40
22.点P(m+3,m+1)直角坐标系的x轴上，则P点坐标为（ ）
A． （0,2） B．(2,0) C．(4,0) D． (0,-4)
23.下列说法正确错误的是（ ）
A．如果一组数据的众数是5,那么这组数据出现次数最多的是5。
B．一组数据的平均数，众数，中位数有可能相同。
C．一组数据的中位数有且只有一个。
D．一组数据的平均数一定大于其中的每一个数据
|
|
一边游泳，甲的速度是3米/秒，乙的速度是2米/秒，图中的实线
和虚线分别为甲乙在游泳池一边距离随时间的变化而变化的图象，
若不计转向时间，则从开始起到3分钟止，他们相遇的次数为（ ）
25．已知一个多边形的的内角和为1080º，则这个多边形的边数是（ ）
A．8 B．7 C．6 D．5
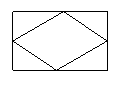26.如图，顺利连结矩形ABCD的各边中点，得到菱形EFGH，这个由矩形和菱形组成的图形（ ）
A．是轴对称图形但不是中心对称图形
B．是中心对称图形但不是轴对称图形
C．是中心对称图形又是轴对称图形
D．没有对称性×√∥
27．已知四边形ABCD中，AC与BD交于点O,如果只给出条件“AB//CD”，那么还不能判定ABCD为平行四边形。给出下列四种说法，①如果再加上条件“BC=AD”,那么四边形ABCD一定是平行四边形，②如果再加上一个条件“∠BAD=∠BCD”,那么四边形ABCD一定是平行四边形，③如果再加上条件“AO=CO”那么四边形ABCD一定是平行四边形，④如果再加上一个条件“∠DBA=∠CAB”,那么四边形ABCD一定是平行四边形，其中正确的是（ ）
A．①和② B．①③和④ C．②和③ D．②③和④
29．已知一次函数y=3x+6与x交于A点，与y轴交于B点，试求△AOB的面积（O为坐标原点）
30．某商场一天中售出李宁牌运动鞋16双，其中各种尺码的鞋销售量如下表所示：
| 鞋的尺码(cm) | 23.5 | 24 | 24.5 | 25 | 26 |
| 销售量（双） | 1 | 3 | 4 | 6 | 2 |
则这16双鞋的尺码组成的一组数据中：
① 众数和中位数是多少？
② 通过计算：如果商场10天进一次货，对李宁牌以上尺码的运动鞋怎么进货？并说明理由？
31．已知菱形的两条对角线长的和为8
，周长为8cm，求菱形的面积。
32.某工厂要把一批产品从A运往B地，若通过铁路运输，则每千米需交运费15元，还要交装卸费400元及手续费200元，若通过公路运输，则每千米需要交运费25元，还需交手续费100元（由于本厂职工装卸，不需交装卸费）。设A地到B地的路程为X km，通过铁路运输和通过公路运输需交总运费Y1元和Y2元，
（1）求Y1和Y2关于x可以节省总运费。
（2）问哪种运输可以节省总运费
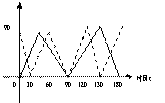
33．某气象研究中心观测一场沙尘暴从发生到结束的全过程，开始时风速平均每小时增加2千米，4小时后，沙尘暴经过开阔荒地，风速变为平均每小时增加4千米，一段时间后，风速保持不变，当沙尘暴遇到绿色植被时，其风速平均每小时减少1千米，最终停止，结合风速与时间关系图象，回答下列问题：
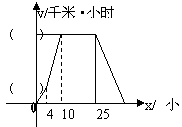⑴在y轴的（ ）内填入相应的数值
⑵沙尘暴从发生到结束，共经过多少小时？
⑶求出当x≥25时，风速y（千米/小时）与时间x之间的关系式。
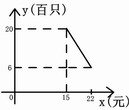34、（本题10分）已知某种型号的计算器进价是每只14元，每月平均销量y（百只）与销售价x（元）的关系如图，销售成本每月4600元。⑴求y关于x的函数关系式。⑵当售价是每只19.5元时，销售这种计算器每月可获利多少元？⑶当每只售价分别是19.5元和22元时，试比较该店每月获利的多少？
35．（本小题满分9分）
甲、乙两件服装的成本共500元，商店老板为获取利润，决定将甲服装按50﹪的利润定价，乙服装按40﹪的利润定价。在实际出售时，应顾客要求，两件服装均按9折出售，这样商店共获利157元，求甲、乙两件服装的成本各是多少元？
36．如图，正方形纸片ABCD的BC边上有一点E，AE=10㎝．若把纸片沿AE的中垂线折叠，使点E与点A重合，你能求出纸片上折痕MN的长吗？解释你的方法．
 |
37．（本小题满分9分）
甲、乙两件服装的成本共500元，商店老板为获取利润，决定将甲服装按50﹪的利润定价，乙服装按40﹪的利润定价。在实际出售时，应顾客要求，两件服装均按9折出售，这样商店共获利157元，求甲、乙两件服装的成本各是多少元？
38、(本题满分10分)
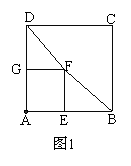
已知正方形ABCD和正方形AEFG有一个公共点A,点G、E分别在线段AD、AB上.
(1) 如图1, 连结DF、BF,若将正方形AEFG绕点A按顺时针方向旋转,判断命题:“在旋转的过程中线段DF与BF的长始终相等.”是否正确,若正确请证明,若不正确请举反例说明;
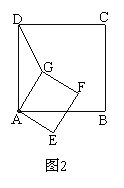
(2) 若将正方形AEFG绕点A按顺时针方向旋转, 连结DG,在旋转的过程中,你能否找到一条线段的长与线段DG的长始终相等.并以图2为例说明理由.
 |  | ||