八年级（上）数学第一学期期末调研测试卷
一、 选择题
1．下列各数中是无理数的是（ ）
A、2
B、
C、
D、
2．9的平方根是（ ）
A、3
B、－3
C、±3
D、±
3．将下列长度的三根木棒首尾顺次连接，能组成直角三角形的是（ ）
A、1、2、3 B、2、3、4 C、3、4、5 D、4、5、6、
4．下列图案中，是中心对称图形的是（
）
5．位于坐标平面上第四象限的点是（ ）
A、（0，－4） B、（3，0） C、（4，－3） D、（－5，－2）
6．根据下列表述，能确定位置的是（ ）
A、某电影院2排 B、南京市大桥南路
C、北偏东30° D、东经118°，北纬40°
X=2
7．已知 是方程kx－y=3的一个解，那么k的值是（ ）
y=1
A、2 B、－2 C、 1 D、－1
8．下列一次函数中，y的值随着x值的增大而减小的是（
）
A、y=x B、y=－x C、y=x+1 D、y=x－1
9．如图，将两块全等的含30°角的直角三角板拼接在一起，这个图形可以看作是由一块直角板绕着直角顶点经过一次旋转后得到的，那么旋转的角度可以是（ ）
A、30° B、60° C、90° D、180°
10．甲、乙两人参加植树活动，两人共植树20棵，已知甲植树数是乙的1.5倍，如果调甲植树x棵，乙植树y棵，那么可以列方程组（ ）
x+y=20 x=20+y
x+y=20
x+y=20
A、 B、 C、 D、
X=2.5y x=1.5y x=1.5y x=y+1.5
二、 填空题
11．如果一次函数y=x+b经过点A（0，3），那么b=________________
12．某中学举行广播操作赛，六名评委对某班打分如下：
7.5分，8.2分，7.8分，9.0分，8.1分，7.9分
去掉一个最高分和一个最低分后的平均分是____________分
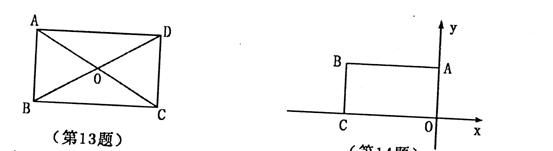13．如图，在矩形ABCD中，两条对角线AC、BD相交于点O，AB=OA=4，则AD=__________
14．如图，矩形ABCDO中，C、A两点的坐标分别为（－4，0）、（0，2），则B点的坐标是（ ）
15．写出两个无理数，使这两个无理数的积为有理数，那么这两个无理数可以是__________、___________________
三、 化简
16．
－3
17．（3+）
四、 解方程组
y=2x
18．
x－y=1
x+y=4
19.
2x－y=－1
五、 解下列各题
20．对于边长为2的正△ABC，建立适当的直角坐标系，写出各个顶点的坐标。
21．在平面直角坐标系中，将坐标是（0，4），（1，0），（2，4），（3，0），（4，4）的点用线段依次连接起来形成一个图案
（1）在下列坐标系中画出这个图案
（2）若将上述各点的横坐标保持不变，纵坐标分别乘以－1，再将所得各个点用线段依次连接起来，所得的图案与原图案相比有什么变化？
22．蜡烛燃烧，每小时耗去4.8厘米，已知蜡烛原来的长度为24厘米，设燃烧x小明后剩下的长度为y厘米
（1）写出y与x之间的函数关系式
（2）经过多长时间后，蜡烛燃烧完？
23．某运动鞋专柜在一天中销售的运动鞋尺码如下：
| 尺码 | 17 | 21 | 22 | 23 | 24 |
| 数量 | 1 | 1 | 5 | 2 | 1 |
（1）求销售的运动鞋尺码的平均数、众数和中位数；
（2）你认为该专柜应当多进什么尺码的运动鞋？
六、 列方程组解应用题
24．小颖和她的爸爸一起玩篮球游戏，两人商定规则为：小颖设中1个得3分，爸爸投中1个得1分，结果两人一共投中了20个，一计算，发现两人的得分刚好相等，你知道他们两人各投中几个吗？
七、
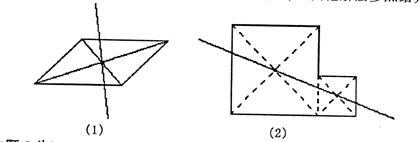
24．封闭的中心对称图形都可以过对称中心作一条直线把它分成面积相等的两部分，
例如：经过圆心的直线把圆分成面积相等的两部分，如图
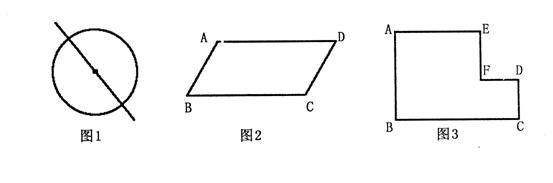请你在图2、图3中分别画一条直线将它们分成面积相等的两部分，其中图2是平行四边形，图3中，∠A=∠B=∠C=∠D=∠E=∠EFD=90°
八、
26．某学校准备添置一批电脑。
方案1：在本地购买，每台需要7000元；
方案2：到外地购买，每台需要6000元，另外需要支付运输费等其它费用总计3000元
设学校需要添置电脑x台，方案1与方案2的费用分别为y
、y
元
（1）分别写出y与x之间的关系式及y与x之间的关系式
（2）当学校添置多少台电脑时，两种方案的费用相同？
（3）如果学校需要添置电脑50台，那么采用哪一种方案较省钱？说说你的理由。
九
27．如图，等腰梯形ABCD中，AD∥BC，AB=CD，AD=10cm,BC=30cm，动点P从点A开始沿AD边向点以每秒1cm的速度运动，同时动点Q从点C开始沿CB边向点B以每秒3cm的速度运动，当其中一点到达端点时，另一点也随之停止运动，设运动时间为t秒
（1）t为何值时，四边形ABQP是平行四边形？
（2）四边形ABQP能成为等腰梯形吗？如果能，求出t的值；如果不能，请说明理由
十、附加题
28．如图，在直角坐标系中，y轴上有一个机器人在A处发现有一个小球在B处沿x轴向坐标原点匀速直线滚动，机器人立即从A处沿直线匀速出发去截小球，如果小球滚动的速度与机器人行走的速度相等
（1）试在图中画出机器人能最快截住小球的位置C，并写出画图方法
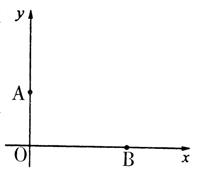（2）如果A点坐标是（0，1），B点坐标（，0），问机器人最快截住小球的位置C的坐标。
参考答案
一、选择题
1．B 2、C 3、C 4、B 5、C
6、D 7、A 8、B 9、C 10、C
二、填空题
11、3
12、8
13、4
14、（－4，2）
15、答案不唯一，可以是形如b
和c，或者+
和－等等
三、化简
16。、解：原式=
－3
=1
17、解：原式=3+2×3×+()
=9+6+2
=11+6
四、解方程组
18、解：将①代入②，得 x－2x=1
－x=1
x=－1
将x=－1代入①得y=－2
x=－1
所以原方程组的解是
y=－2
19、解：①+②，得3x=3
x=1
将x=1代入①,得1+y=4
y=3
x=1
所以原方程组的解是
y=3
五、解下列各题
20、解法一、如图，以边BC所在直线为x轴，以边BC的中垂线为y轴，建立直角坐标系
此时B、C点的坐标分别为（－1，0）、（1，0）
在Rt△ABO中，AB=2，BO=1，则AO=
=
所以A点的坐标为（0，）
解法二：以点B为坐标原点，以边BC所在直线为x轴，建立直角坐标系，则A（1，）、B（0，0）、C（2，0）可仿照解法一给分。
21、解：（1）画出符合要求的图形
（2）所得的图案与原图案关于x轴对称
22、解：（1）y=24－4.8x
(2)当x=5时，y=0，因此经过5小时后，蜡烛点完
23、解：（1）销售的运动鞋尺码的平均数、众数和中位数分别是21.8、22、22
(2)因为尺码为22的运动鞋卖得最多，所以应多进22码的运动鞋。
六、列方程组解应用题
24、解：设小颖投中x个，爸爸投中y个
x+y=20
①
根据题意，得
3x=y ②
x=5
解这个方程组，得
y=15
所以小颖投中5个，爸爸投中15个
七
25、解：如图（1）先作出平行四边的对角线，经过对角线的交点任意作一条直线
如图（2），先作出两个正方形的中心，经过这两个中心作直线，即为所求（也可以延长AE、CD交于H，分别作出矩形ABCH和矩形EFDH的对称中心P、Q，作直线PQ即可）
八、
26、解：(1)y=7000x；y=6000x+3000
(2)由7000x=6000x+3000，解得x=3
因此当学校添置3台电脑时，两种方案的费用相同
（3）当x=50时，y=7000×50=350000；y=6000×50+3000=303000
因为303000<350000，所以采用方案2较省钱
九、
27、解：（1）因为一组对边平行且相等的四边形是平行四边形
所以当AP=BQ时，四边形ABQP是平行四边形
此时，t=30－3t，解得t=7.5(秒)
所以t为7.5秒时，四边形ABQP是平行四边形
（2）四边形ABQP能成为等腰梯形
因为四边形ABCD是等腰梯形，所以四边形CDPQ是平行四边形。则由PD=CQ
得10－t=3t，解得t=2.5(秒)
即t为2.5秒时，四边形ABQP成为等腰梯形
十、附加题
28、（1）画法：连结AB，画线段AB的垂直平分线交x轴于C点
画图正确
（2）设机器人最快可在C(x，0)处截住小球，则OC=x
因为OB=，OA=1，所以BC=－x
由（1）画法可知：AC=BC=－x
在Rt△AOC中，AC=OC+AO。则（－x）=x+1
即－2x+3=1 ，解得x=
所以C点坐标是（，0）