一次函数复习试题

一次函数复习试题

1．点A(2，4)在正比例函数的图象上，这个正比例函数的解析式是　　　　　

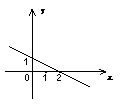
2．若函数(为常数)的图象如图所示，那么当时，的取值范围是（　）

A、　B、　　　C、　D、

3．点A（5，y₁）和B（2，y₂）都在直线y＝－x上，则y₁与y₂的关系（　）

A、y₁≥ y₂B、y₁＝ y₂ C、y₁ ＜y₂ D、y₁ ＞y₂

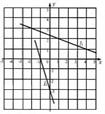4．如图，是在同一坐标系内作出的一次函数y₁、y₂的图象l₁、l₂，设y₁＝k₁x＋b₁，y₂＝k₂x＋b₂，则方程组的解是_______.

A、　　 B、

C、　　 D、

5．在某地，人们发现某种蟋蟀1分钟所叫次数与当地温度之间近似为一次函数关系。下面是蟋蟀所叫次数与温度变化情况对照表：

蟋蟀叫次数	…	84	98	119	…
温度（℃）	…	15	17	20	…

（1）根据表中数据确定该一次函数的关系式；

（2）如果蟋蟀1分钟叫了63次，那么该地当时

的温度大约为多少摄氏度？

某软件公司开发出一种图书管理软件，前期投入的开发、广告宣传费用共50000元，且每售出一套软件，软件公司还需支付安装调试费用200元.

（1）试写出总费用y(元)与销售套数x(套)之间的函数关系式；

（2）如果每套定价700元，软件公司至少要售出多少套软件才能确保不亏本？

6．将直线y=2x向上平移两个单位，所得的直线是（　 ）

A、y=2x+2　　　 B、y=2x-2　 C、y=2（x-2）　 D、y=2（x+2）

7．已知一次函数y = ax +b(a，b是常数)，x与y的部分对应值如下表：

x	－2	－1	0	1	2	3
y	6	4	2	0	－2	－4

那么方程ax + b = 0的解是___________；不等式ax + b＞0的解集是____________.

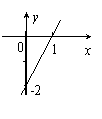8．．已知一次函数y=kx+b的图象如图，当x＜0时，y的取值范围是（　 ）

A、y＞0　　　 B、y＜0　 C、2＜y＜0　　　 D、y＜2

9．老师给出一个函数，甲、乙、丙各正确指出了这个函数的一个性质：甲：函数的图象经过第一象限；乙：函数的图象经过第三象限；丙：在每个象限内，y随x的增大而减小．

请你根据他们的叙述构造满足上述性质的一个函数：　　　　　　　　　　　　  ．

10．某纺织厂生产的产品,原来每件出厂价为80元,成本为60元.由于在生产过程中平均每生产一件产品有0.5米³的污水排出,现在为了保护环境,需对污水净化处理后再排出.已知每处理1米³污水的费用为2元,且每月排污设备损耗为8000元.设现在该厂每月生产产品x件,每月纯利润y元：

①求出y与x的函数关系式.(纯利润=总收入-总支出)

②当y=106000时,求该厂在这个月中生产产品的件数.

11． 如图，某种旅行帽的帽沿接有两个塑料帽带，其中一个塑料帽带上有7个等距的小圆柱体扣，另一个帽带上扎有七个等距的扣眼，下表列出的是用第一扣分别去扣不同扣眼所测得帽圈直径的有关数据(单位：cm)；

扣眼号数(x)	1	2	3	4	5	6	7
帽圈直径(y)	22.92	22.60	22.28	21.96	21.64	21.32	21.00

⑴求帽圈直径y与扣眼号数x之间的一次函数关系式；

⑵小强的头围约为68.94cm，他将第一扣扣到第4号扣眼，你认为松紧合适吗？

12．某产品每件成本10元，试销阶段每件产品的日销售价（元）与产品的日销售量（件）之间的关系如下表：

（元）	15	20	25	30	…
（件）	25	20	15	10	…

（1）在草稿纸上描点，观察点的颁布，建立与的恰当函数模型。

（2）要使每日的销售利润最大，每件产品的销售价应定为多少元？此时每日销售利润是多少元？

]

13． (1)　甲品牌拖拉机开始工作时,油箱中有油30升.如果每小时耗油6升,求油箱中的余油量y（升）与工作时间x(时)之间的函数关系式.

(2)　如图,线段AB表示乙品牌拖拉机在工作时油箱中的余油量y(升)与工作时间x(时)之间的函数关系的图象. 若甲、乙两种品牌的拖拉机在售价、质量、性能、售后服务等条件上都一样.根据图象提供的信息,你愿意购买哪种品牌的拖拉机,并说明理由.

14．某地电话拨号入网有两种收费方式，用户可以任选其一：

（A）计时制：0.05元/分；（B）包月制：50元/月（限一部个人住宅电话上网）．

此外，每一种上网方式都得加收通信费0.02元/分．

（1） 请你分别写出两种收费方式下用户每月应支付的费用y（元）与上网时间x（小时）之间的函数关系式；

（2）　若某用户估计一个月内上网的时间为20小时，你认为采用哪种方式较为合算？

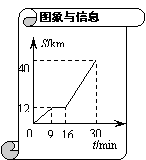
15． 如图是某汽车行驶的路程S(km)与时间t(min) 的函数关系图.观察图中所提供的信息，解答下列问题：

（1）汽车在前9分钟内的平均速度是多少？　　（2）汽车在中途停了多长时间？

（3）当16≤t≤30时，求S与t的函数关系式.

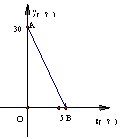
16．如图，直线与轴交于点(－4,0)，则>0时，的取值范围是(　　)

A、>－4　B、>0　　 C、<－4 　　　D、<0

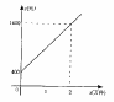
17．某公司市场营销部的营销人员的个人月收入与该营销员每月的销售量成一次函数关系，其图像如图所示.根据图像提供的信息，解答下列问题：

（1）求出营销人员的个人月收入y元与该营销员每月的销售量x万件（x≥0）之间的函数关系式；（2）已知该公司营销员李平5月份的销售量为1.2万件，求李平5月份的收入.

18．大连市内与庄河两地之间的距离是160千米，若汽车以平均每小时80千米的速度从大连市内开往庄河，则汽车距庄河的路程y(千米)与行驶的时间x(小时)之间的函数关系式为_______________________________；

19．某出版社出版适合中学生阅读的科普读物，该读物首次出版印刷的印数不少于5000册时，投入的成本与印数间的相应数据如下：

印数x(册)	5000	8000	10000	15000	…
成本y(元)	28500	36000	41000	53500	…

(1)　　　 发过对上表中数据的探究，发现这种读物的投入成本y (元)是印数x (册)的一次函数，求这个一次函数的解析式(不要求写出x的取值范围)。

(2)　　 如果出版社投入成本48000元，那么能印该读物多少册？

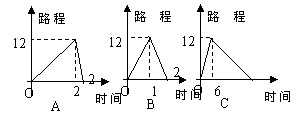
20．百舸竞渡，激情飞扬。端午节期间，某地举行龙舟比赛。甲、乙两支龙舟队在比赛时路程y（米）与时间x（分钟）之间的函数图象如图所示。根据图象回答下列问题：

（1）1.8分钟时，哪支龙舟队处于领先位置？

（2）在这次龙舟赛中，哪支龙舟队先到达终点？先到达多少时间？

（3）求乙队加速后，路程y（米）与时间x（分钟）之间的函数关系式。

21．已知某山区的平均气温与该山的海拔高度的关系见下表：

海拔高度（米）	0	100	200	300	400	500	…
平均气温（℃）	22	21.5	21	20.5	20	19.5	…

（１）若海拔高度用（米）表示，平均气温用（℃）表示，试写出与之间的函数关系式；

（２）若某种植物适宜生长在18℃～20℃(包含18℃,也包含20℃)山区,请问该植物适宜种植在海拔为多少米的山区?

1.函数中，自变量x的取值范围是　　　 。

2.函数y=中，自变量x的取值范围是___________；

3．函数的自变量x的取值范围是　　　　  .

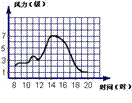
4.沈阳市的春天经常刮风，给人们的出行带来很多不便，小明观测了4月6日的连续12个小时的风力变化情况，并画出了风力随时间变化的图象，则下列说法正确的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

A、在8时至14时，风力不断增大　　  B、 在8时至12时，风力最大为7级

C、8时风力最小　　　　　　 D、20时风力最小

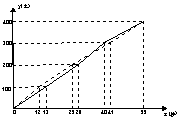5.  4×100米拉力赛是学校运动会最精彩的项目之一。图中的实线和虚线分别是初三（1）班和初三（2）班代表队在比赛时运动员所跑的路程y(米)与所用时间x(秒)的函数图象(假设每名运动员跑步速度不变，交接棒时间忽略不计)。

问题：

⑴初三（2）班跑得最快的是第______接力棒的运动员；

⑵发令后经过多长时间两班运动员第一次并列？

　

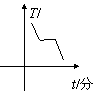
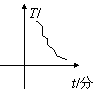
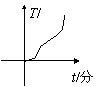
6.蜡是非晶体，在加热过程中先要变软，然后逐渐变稀，然后全部变为液态，整个过程温度不断上升,没有一定的熔化温度，如图所示，四个图象中表示蜡溶化的是

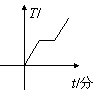A、 　　　　　　　　　 B、　

C、　　　　　　 　　　 D、

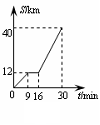
7.　如图是某汽车行驶的路程S(km)与时间t(min) 的函数关系图.观察图中所提供的信息，解答下列问题：　 （1）汽车在前9分钟内的平均速度是多少？

（2）汽车在中途停了多长时间？　　（3）当16≤t≤30时，求S与t的函数关系式.8. 函数的自变量x的取值范围是　　　　  .

9. 函数中，自变量x的取值范围是（　）

A、x>3　B、x≥3　 C、x>-3　 D、x≥-3

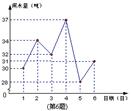
10. 某住宅小区六月份中1日至6日每天用水量变化情况如图所示，那么这6天的平均用水量是（　　）

A、30吨　B、31吨 C、32吨 D、33吨

11．水池有2个进水口，1个出水口，每个进水口进水量与时间的关系如图甲所示，出水口出水量与时间的关系如图乙所示．某天O点到6点，该水池的蓄水量与时间的关系如图丙所示．

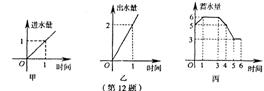下列论断：①O点到1点，打开两个进水口，关闭出水口；②1点到3点，同时关闭两个进水口和一个出水口；③3点到4点，关闭两个进水口，打开出水口；④5点到6点，同时打开两个进水口和一个出水口．其中，可能正确的论断是(　 )

(A)①③ (B)①④ (C)②③ (D)②④

12．用一水管向图中容器内持续注水，若单位时间内注入的水量保持不变，则在注满容器的过程中，容器内水面升高的速度

A、保持不变　　　B、越来越慢

C、越来越快　　　D、快慢交替变化

13．2004年6月3日中央新闻报道,为鼓励居民节约用水,北京市将出台新的居民用水收费标准:①若每月每户居民用水不超过4立方米,则按每立方米2元计算;②若每月每户居民用水超过4立方米,则超过部分按每立方米4.5元计算(不超过部分仍按每立方米2元计算).现假设该市某户居民某月用水立方米,水费为元,则与的函数关系用图象表示正确的是（　 ）

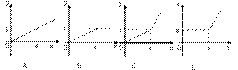14．小明、爸爸、爷爷同时从家里出发到达同一目的地后立即返回，小明去时骑自行车，返回时步行；爷爷去时是步行，返回时骑自行车；爸爸往返都是步行。三人步行的速度不等，小明和爷爷骑自行车的速度相等，每个人的行走路程与时间的关系如图9中的A、B、C表示，根据图象回答下列问题：（1）三个图象中哪个对应小明、爸爸、爷爷？（2）小明家距离目的地多远？

（3）小明与爷爷骑自行车的速度是多少？爸爸步行的速度是多少？

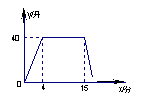
10．某洗衣机在洗涤衣服时，经历了进水、清洗、排水、脱水四个连续过程，其中进水、清洗、排水时洗衣机中的水量y(升)与时间x(分钟)之间的关系如折线图所示：

根据图象解答下列问题

（1）洗衣机的进水时间是多少分钟？清洗时洗衣机中的水量是多少升？

（2）已知洗衣机的排水速度为每分钟19升， ①求排水时y与x之间的关系式。②如果排水时间为2分钟，求排水结束时洗衣机中剩下的水量。

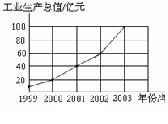
 2．（2004鹿泉）右图是根据某市1999年至2003年工业生产总值绘制的折线统计图.观察统计图可得：增长幅度最大的年份是　　　年，比它的前一年增加　　　亿元.

3．（2004南宁） 如图，l₁反映了某公司的销售收入与销售量的关系，l₂反映了该公司产品的销售成本与销售量的关系，当该公司赢利（收入大于成本）时，销售量（）

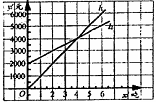A 小于3吨　　B 大于3吨　

C 小于4吨　 D 大于4吨

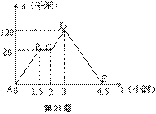
6．（2004无锡）如图中的图象（折线ABCDE）描述了一汽车在某一直线上的行驶过程中，汽车离出发地的距离s（千米）和行驶时间t（小时）之间的函数关系，根据图中提供的信息，给出下列说法：①汽车共行驶了120千米；②汽车在行驶途中停留了0.5小时；③汽车在整个行驶过程中的平均速度为千米/时；④汽车自出发后3小时至4.5小时之间行驶的速度在逐渐减少.其中正确的说法共有（　　  ）

A、1个　 B、2个　 C、3个　 D、4个

7．（2005常州）某水电站的蓄水池有2个进水口，1个出水口，每个进水口进水量与时间的关系如图甲所示，出水口出水量与时间的关系如图乙所示.已知某天0点到6点,进行机组试运行,试机时至少打开一个水口,且该水池的蓄水量与时间的关系如图丙所示:

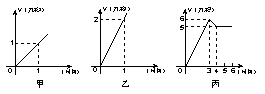
给出以下3个判断:

①0点到3点只进水不出水；②3点到4点,不进水只出水；③4点到6点不进水不出水. 则上述判断中一定正确的是（　）

A、①　　B、②　　C、②③　 D、①②③