勾股定理检测题
班级________ 姓名__________总分_______
一、填空题：（每空2分，共28分）
1. 若直角三角形两直角边之比为3∶4，斜边的长为25cm，则这个直角三角形的面积是________________.
2.
在△ABC中，
，
（m>n），当c=__________时，∠B=90°.
3.
在△ABC中，∠C=90°，BC=12，
，则AC=_________.
4. 在△ABC中，AB=AC=17cm，BC=16cm，AD⊥BC于D，则AD=___________cm.
5.
若三角形的三边长a、b、c满足
，则此三角形是______三角形.
6. 一棵树从离地面3米处断裂，树顶落在离树根部4米处，则树高为 米.
7. 以一个直角三角形的一条直角边为边长的正方形的面积为225，以这个直角三角形的斜边为边长的正方形的面积为625，则以这个直角三角形的另一条直角边为边长的正方形的面积为____________.
8. 消防云梯的长度是34米，在一次执行任务时,它只能停在离大楼16米远的地方,则云梯能达到大楼的高度是 米.
9.
有一根长24 cm的小木棒，把它分成三段，组成一个直角三角形，且每段的长度都是偶数,则三段小木棒的长度分别是________cm 、_________cm 、_________cm.
10. 在Rt△ABC中，∠C=90°，c=34，a:b=8:15，则a=_______，b=_______.
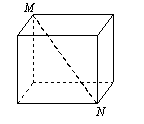
11. 如图所示，长方体底面长为4，宽为3，高为12，求长方体对角线MN的长为_______.
二、选择题：（每题2分，共18分）
12. 把直角三角形的两条直角边同时扩大到原来的2倍，则斜边扩大到原来的（ ）
A. 2倍 B. 4倍 C. 6倍 D. 8倍
13、分别以下列四组数为一个三角形的边长：(1)0.6、0.8、1；(2)5、12、13；
(3)8、15、17；(4)4、5、6其中是能构成直角三角形的勾股数有( )。
A．4组 B．3组 C．2组 D．1组
14、下列条件中，不能确定三角形是直角三角形的是（ ）
A. 三角形中有两个角是互为余角 B. 三角形三个内角之比为3∶2∶1
C. 三角形的三边之比为3∶2∶1 D. 三角形中有两个内角的差等于第三个内角
15下列说法中，错误的是（ ）
A. △ABC中，若∠B=∠C－∠A，，则△ABC是直角三角形
B. △ABC中，a2=(b+c)(b－c), 则△ABC是直角三角形
C．△ABC中，∠A:∠B:∠C=3:4:5, 则△ABC是直角三角形
D. △ABC中，a:b:c=3:4:5, 则△ABC是直角三角形
16、在△ABC中，∠C=90°，周长为60，斜边与一直角班的比为13∶5，则这个三角形的三边长分别为（ ）
A. 5，4，3 B. 13，12，5 C. 26，24，20 D. 26，24，10
17、以面积为9cm2的正方形的对角线为边，作一个正方形，其面积为（ ）
A. 9cm2 B. 12cm2 C. 18cm2 D. 249m2
18、如果△ABC的三边分别为
，
，
（m>1），那么（ ）
A △ABC是直角三角形，且斜边长为
B △ABC是直角三角形，且斜边长为
C △ABC是直角三角形，但斜边长需由m的大小确定
D △ABC不是直角三角形
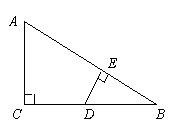
19、如图所示，△ABC中，∠C=90°，D为BC边的中点，DE⊥AB于E，则
等于（ ）
A. 
B.
C. 
D. 
20、等腰三角形底边上的高为4cm，周长为16cm，则三角形的面积为（ ）
A. 14cm2 B. 12 cm2 C. 10 cm2 D. 8 cm2
三、解答题：（共54分）
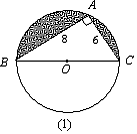
21、（10分）求下列图形中阴影部分的面积.
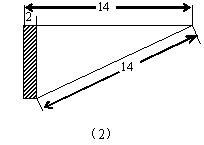
22、（6分）某人步行向北走了2公里，接着又向正东方向走了1.5公里，则他此时离出发地点多远？
23、（6分）如图所示，△ABC中，D为BC边上一点，若AB=13，BD=5，AD=12，BC=14，求AC的长.
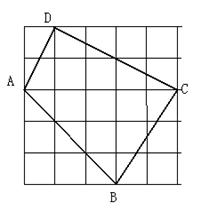
24、（8）如图，每个小方格都是边长为1的正方形，求图中格点四边形ABCD的周长和面积。
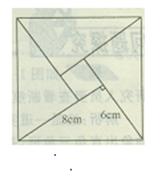25、（8）由四个完全相同的直角三角形拼得一个大正方形，如图3-1．已知直角三角形两条直角边分别是6cm，8cm，求大正方形的面积。(用两种方法解)
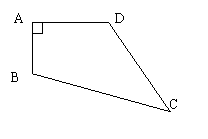
26、（8分）已知，如图，四边形ABCD中，AB=3cm，AD=4cm，BC=13cm，CD=12cm，且
∠A=90°，求四边形ABCD的面积。
 |
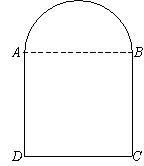
27、 （8分）某工厂的大门如图所示，其中四边形ABCD是长方形，上部是以AB为直径的半圆，已知AD=2.3米，AB=2米，现有一辆装满货物的卡车，高2.5米，宽1.6米，问这辆汽车能否通过大门？请说出你的理由.
