平行四边形复习题
一、填空题：
1．菱形两条对角线分别长6cm，8cm，则菱形边长为 ；
2．如图，在⊿ABC中，AD⊥BC于D，E、F分别是AB、AC的中点，当⊿ABC满足条件 时，AEDF是菱形；
3．如图，在平行四边形ABCD中，EF∥BC，GH∥AB，EF、GH的交点P在BD上，图中有 对四边形面积相等；他们是 。
4.矩形的两条对角线的夹角为
,较短的边长为12
,则对角线长为 .
5.根据图中所给的尺寸和比例,可知这个“十”字标志的周长为
.
6.已知菱形的两条对角线长为12和6,那么这个菱形的面积为 
.
7．如图,
是四边形ABCD的对称轴,如果AD∥BC,有下列结论: (1)AB∥CD;(2)AB=CD;(3)AB
BC;(4)AO=OC.其中正确的结论是
.
(把你认为正确的结论的序号都填上)
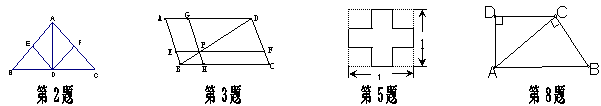8．如图，已知梯形ABCD中，AB∥CD，AD⊥CD，若腰BC=15，对角线AC=20，且AC⊥BC，则AB=
，AD= ，CD= ，
。
二、选择题
1.已知平行四边形ABCD，AC、BD是对角线，下列结论中不一定正确的是（ ）；
A． AB=CD； B． AC=BD； C． AC⊥BD时，它是菱形； D． 当∠ABC=90°时，它是矩形
2.能够找到一点，使该点到各边距离都相等的是（ ）
①平行四边形 ②菱形 ③矩形 ④正方形 ⑤三角形
A．①② B．②③④⑤ C． ②④ D． ②④⑥
3.用一批形状完全相同的正多边形的地板砖铺地面，要求顶点聚在一起，且砖与砖之间不留空隙，现有：①正三角形；②正四边形；③正五边形；④正六边形；四种形状的地板砖，则符合要求的有：
A．①②③； B。①②④； C。②③④； （D）①③④；
4.菱形周长为40，两邻边所夹锐角为30°，则菱形的面积为（ ）
A．30； B．40； C．50； D．60；
5.顺次连结矩形的各边中点，所得四边形是（ ）
A． 平行四边形； B．矩形； C．菱形； D．正方形；
6.有两个角相等的梯形是（ ）
A． 等腰梯形； B．直角梯形； C．一般梯形； D．等腰梯形或直角梯形；
7.小红画了两条相等并且垂直的线段，以它们为对角线的四边形是（ ）
A． 平行四边形； B．菱形； C．正方形； D．无法确定
8．在平行四边形ABCD中，∠A：∠B：∠C：∠D的值可以是（ ）
A．1：2：3：4 B． 3：4：4：3 C． 3：3：4：4 D ．3：4：3：4
9．能确定平行四边形的大小和形状的条件是（ ）
A．已知平行四边形的两邻边 B．已知平行四边形的两邻角
C．已知平行四边形的两条对角线 D．已知平行四边形的的两边及夹角
10.在线段、角、等边三角形、等腰三角形、平行四边形、矩形、菱形、正方形、圆、等腰梯形这十种图形中,既是轴对称图形又是中心对称图形的共有 ( )
A.4种 B.5种 C.7种 D.8种
11.下列说法中,错误的是 ( )
A.平行四边形的对角线互相平分 B.对角线互相平分的四边形是平行四边形
C.菱形的对角线互相垂直 D.对角线互相垂直的四边形是菱形
12.给出四个特征(1)两条对角线相等;(2)任一组对角互补;(3)任一组邻角互补;(4)是轴对称图形但不是中心对称图形,其中属于矩形和等腰梯形共同具有的特征的共有 ( )
A.1个 B.2个 C.3个 D.4个
13.如果一个四边形的两条对角线互相平分,互相垂直且相等,那么这个四边形是 ( )
A.矩形 B.菱形 C.正方形 D.菱形、矩形或正方形
14.如图,矩形ABCD沿着AE折叠,使D点落在BC边上的F点处,如果
,则
等于（ )
A.
B.
C.
D.
15.已知四边形ABCD中,AC交BD于点O,如果只给条件“AB∥CD”,那么还不能判定四边形ABCD为平行四边形,给出以下四种说法:
(1)如果再加上条件“BC=AD”,那么四边形ABCD一定是平行四边形;
(2)如果再加上条件“
”,那么四边形ABCD一定是平行四边形;
(3)如果再加上条件“AO=OC”,那么四边形ABCD一定是平行四边形;
(4)如果再加上条件“
”,那么四边形ABCD一定是平行四边形
其中正确的说法是( )
A.(1)(2) B.(1)(3)(4) C.(2)(3) D.(2)(3)(4)
16．下列美丽的图案，既是轴对称图形又是中心对称图形的个数是
 |
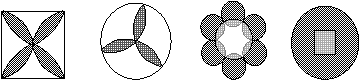A．1个 B．2个 C．3个 D．4个
17．下列命题中，正确命题是（ ）
A．两条对角线相等的四边形是平行四边形；
B．两条对角线相等且互相垂直的四边形是矩形；
C．两条对角线互相垂直平分的四边形是菱形；
D．两条对角线平分且相等的四边形是正方形。
18．将一圆形纸片对折后再对折，得到图3，然后沿着图中的虚线剪开，
得到两部分，其中一部分展开后的平面图形是( )
三、解答题：
1.工人师傅做铝合金窗框分下面三个步骤进行:
(1)先截出两对符合规格的铝合金窗料(如图①),使AB=CD,EF=GH;
(2)摆放成如图②的四边形,则这时窗框的形状是 形,根据的数学道理是:
;
(3)将直角尺靠紧窗框的一个角(如图③),调整窗框的边框,当直角尺的两条直角边与窗框无缝隙时(如图④),说明窗框合格,这时窗框是 形,根据的数学道理是:
|
(图①) (图②) (图③) (图④)
四、证明题：
1.已知：如图，AD是△ABC的角平分线，DE∥AC与E，
DF∥AB交AC于，请判断四边形AEDF的形状，并说明理由。
2.正方形ABCD中，AE=CF，则四边形BEDF是菱形吗？
请说明理由。