《三角形》、《命题和证明》、《轴对称和等腰三角形》
综合测试卷二
考试时间：100分，满分：100分
班级： 姓名： 得分：
一、填空题（每题4分，共20分）
1、三角形的三边长为3、7、x，则x的取值范围是 。
2、等腰三角形有一个角是70度，则其他两个角的度数是 .
|
|
|
3、如图，AB＝CD，AD＝CB，O为AC上一点，过O任作直线EF分别交AD、BC于E、F，要使BE＝FD,则应满足的条件是 。
4、如图4，已知⊿ABC≌⊿ADE，D是∠BAC的平分线上一点，且∠BAC=60°，
则∠CAE= 。
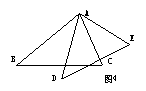
5、如图：，在
ABC中，AB=AC，
，P是ABC内一点，且
PBC= PCA，
则BPC=_____.
二、选择题（每题3分，共30分）
1、△ABC中，AB＝4，AC＝3，若E为BC的中点，AE＝x，则x的取值范围为（ ）
A.3＜x＜4 B.1＜x＜7 C.0＜x＜1 D. x≤1
2、锐角三角形中任意两个锐角的和必大于 ( )。
A 120° B 110° C 100° D 90°
3、若
， AB=6cm，BD=7cm，AD=4cm，那么BC的长为（ ）
A、6 cm B、5 cm C、4cm D、不能确定
4、下列说法中正确的是（ ）
A、轴对称图形是由两个图形组成 B、等边三角形有三条对称轴
C、两个全等三角形能组成一个轴对称图形 D、直角三角形一定是轴对称图形
5、下列命题中正确的是（ ）
①全等三角形对应边相等；②三个角对应相等的两个三角形全等；③三边对应相等的两三角形全等；④有两边对应相等的两三角形全等。
A．4个 B、3个 C、2个 D、1个
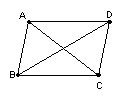
6．如图，已知AB=CD，AD=BC，则图中全等三角形共有（ ）
A．2对 B、3对 C、4对 D 、5对
7、如图，A在DE上，F在DC上，且∠1＝∠2＝∠3，AC＝CE，则DE的等于（ ）
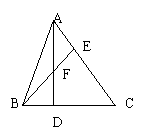A.DC
B.BC
C.AB
D.1
|
|
|
|
|
8、如图，ΔABC中，∠CAB=520，∠ABC=740，AD⊥BC，BE⊥AC，AD，BE交于F，则∠AFB=（ ）度
A、126 B、120 C、116 D、110
9、在钝角三角形ABC中，把AB=AC，D是BC上一点，AD把ABC分成两个等腰三
角形，则BAC的度数为（ ）
A、
B、
C、
D、
10、如图，在ABC中，AB、BC的垂直平分线相交于三角形内一点O，下列结论中，错误的是（ ）
A、点O在AC的垂直平分线上B、AOB、BOC、COA都是等腰三角形
C、OAB+OBC+OCA=
D、点O到AB、BC、CA的距离相等
三、作图题（10分）
1、用一个圆、一个正三角形、一条线段设计一个轴对称图案，并说明你要表达的含义。
2、已知△ABC，求作△
，使∠C=∠
，
= BC，
= AC.（使用尺规作图，并保留作图轨迹，不要求写出作图过程）
 |
四、解答题（40分）
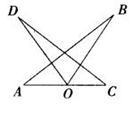
1、（5分）已知：如图，∠AOD=∠BOC，∠B=∠D，O是AC的中点。求证：OB=OD．
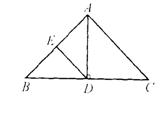
2、（5分）如图，ABC中，AB=AC，AD
BC，DE//AC，试说明BDE和AED都是等腰三角形
3、（5分）如图，已知：在
中，
，
，BD是 的角平分线，求
的度数.
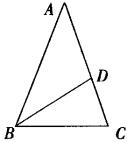
4、（7分）已知：在△ABC中，AB=AC，点D在AC上，且BD=BC=AD，
求∠C的度数。
5、（8分）如图，等腰直角三角形ABC中，∠ACB＝90°，AD为腰CB上的中线，CE⊥AD交AB于E．求证∠CDA＝∠EDB．
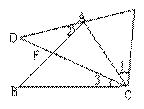
5、（10分）△ABC中，∠MAC为∠BAC的补角，P为∠MAC的平分线上一点（AP段）。
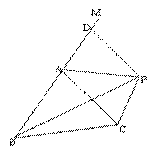①试比较AB＋AC与BP＋PC的大小。②若P在角平分线的反向延长线上，则结论仍然成立吗？