第十七章反比例函数检测题
班级__________ 姓名___________
一、选择题(每小题3分,共30分)
1．下列函数中，y是x的反比例函数的为（ ）
A.
B.
C.
D.
2．反比例函数y=
的图象位于（ ）
A．第一、二象限 B．第一、三象限 C．第二、三象限 D．第二、四象限
3．已知矩形的面积为10，则它的长y与宽x之间的关系用图象表示大致为（ ）
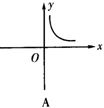
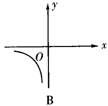
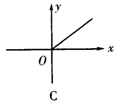
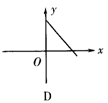
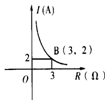4．某闭合电路中，电源电压为定值，电流I（A）与电阻R（Ω）成反比例，如右图所表示的是该电路中电流I与电阻R之间的函数关系的图象，则用电阻R表示电流I的函数解析式为（ ）．
A．I=
B．I=-
C．I=
D．I=
5．若点（3，4）是反比例函数
图象上一点，则此函数图象
必经过点（
）
A.（3，－4） B.（2，－6） C.（4，－3） D. （2，6）
6．在第三象限中，下列函数，y随x的增大而减小的有（ ）。
①、y=-
②、y=
③、y=-2x+5 ④、y=-5x-6
A.1个 B.2个 C.3个 D.4个
7．若函数y=（m+2）xm-3是反比例函数，则m的值是（ ）
A．2 B．-2 C．±2 D．以上答案均不正确
8．若y与x成正比，y与z的倒数成反比，则z是x的（ ）
A.正比例函数 B.反比例函数 C.二次函数 D.z随x增大而增大
9．已知点A（-3，y1），B（-2，y2），C（3，y3）都在反比例函数y=
的图象上，则（ ）
A．y1<y2<y3 B．y3<y2<y1 C．y3<y1<y2 D．y2<y1<y3
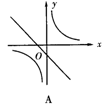
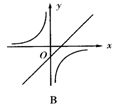
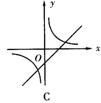
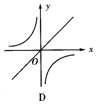
10．已知关于x的函数y=k（x+1）和y=-
（k≠0）它们在同一坐标系中的大致图象是（ ）
二、填空题（每题3分，共30分）
11．已知反比例函数y=（k≠0）的图象经过点P（-2，-1），则该反比例函数的解析式是________．
12.已知
-2与
成反比例，当=3时，=1，则与间的函数关系式为
；
13．已知关于x的一次函数y=kx+1和反比例函数y=
的图象都经过点（2，m），则一次函数的解析式是________．
14．一批零件300个，一个工人每小时做15个，用关系式表示人数x与完成任务所需的时间y之间的函数关系式为________．
15.
是关于的反比例函数，且图象在第二、四象限，则
的值为 ；
16．反比例函数y=（k是常数，k≠0）的图象经过点（a，-a），那么该图象经过第_________象限
17．若m＜-1，则下列函数①y=
（x＞0）；②y=-mx+1；③y=mx； ④y=（m+1）x中，
y随x的增大而增大的是 （填写编号）。
18.若一次函数y=x+b与反比例函数y=图象，在第二象限内有两个交点，则k______0，b_______0，（用“>”、“<”、“＝”填空）
19．已知一次函数y=3x+m与反比例函数y=
的图象有两个交点，当
m=_____时，有一个交点的纵坐标为6．
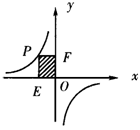
20.如图，P是反比例函数图象在第二象限上的一点，且矩形PEOF的面积 为8，则反比例函数的表达式是_________．
三、解答题
21.(8分)已知点A(0,-6),B(-3,0),C(m,2)三点在同一直线上,试求出图象经过其中一点的反比例函数的解析式并画出其图象(要求标出必要的点,可不写画法)
22.(8分)一司机驾驶汽车从甲地去乙地，以80千米/小时的平均速度用6小时到达目的地.
(1)当他按原路匀速返回时，求汽车速度v(千米/小时)与时间t(小时)之间的函数关系式；(2)如果该司机匀速返回时，用了48小时，求返回时的速度.
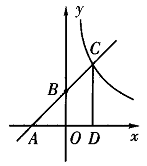23．（8分）如图，已知一次函数y=kx+b（k≠0）的图象与x轴、y轴分别交于A、B两点，且与反比例函数y=
（m≠0）的图象在第一象限交于C点，CD垂直于x轴，垂足为D，若OA=OB=OD=1．
（1）求点A、B、D的坐标;
（2）求直线AB的解析式．
（3）反比例函数的解析式
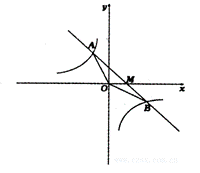
24．（8分）如图，已知一次函数y=kx+b的图象与反比例函数y=-
的图象交于A、B两点，且点A的横坐标和点B的纵坐标都是-2．求：
（1）一次函数的解析式；
（2）△AOB的面积．
（3）根据图象写出使一次函数的值大于反比例函数的 值的x的取值范围．
25.(8分)某厂从2002年起开始投入技术改进资金,经技术改进后,其产品的生产成本不断降低,具体数据如下表:
| 年 度 | 2002 | 2003 | 2004 | 2005 |
| 投入技术改进资金x/万元 | 2.5 | 3 | 4 | 4.5 |
| 每件产品的生产成本y/万元 | 7.2 | 6 | 4.5 | 4 |
(1) 请你认真分析表中数据,从你所学习过的一次函数和反比例函数中确定哪种函数能表示变化规律,并求出它的解析式.
(2) 按照这种变化规律,若2006年已投入技术改进资金5万元;
① 请你预计每件产品的生产成本比2005年降低多少万元.
② 如果打算在2006年把每件产品成本降低到3.2万元,则还需投入技术资金多少万元(结果精确到0.01万元)