中学初二年级数学质量检测 学号 姓名
一、填空:2×18=36
1.
当k 时，函数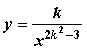
是正比例函数，且图象在第二、四象限内；若一次函数y=（m2－1）x2＋（m-3）x+m+1的图象不经过第三象限，则m的取值是
。
2．反比例函数
的反比例系数为 ，当
＜0时，图象位于第 象限。
3．已知图象
与
的一交点为（a，b），那么另一个交点坐标为
。
4．一次函数
与
轴、
轴的交点分别为A、B，若△OAB的周长为
，（O为坐标原点），则
。
5．一次函数的图象过点（－1，0），且函数值随着自变量的增大而减小，写出一个符合条件的关系式
；如果反比例函数
的图象位于第二、四象限内，那么满足条件的正整数k的值是
。
6一次函数
中，
随的增大而减小，且
，则这个函数的图象经过 象限。点A为直线
上一点，点A到两坐标轴的距离相等，则点A的坐标为
。
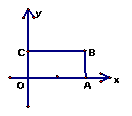7．如图，在直角坐标系中，矩形OABC的顶点B（15，6），
直线
恰好将矩形分成面积相等的两部分，那么
。
8．点P是反比例函数
上的一点，PD^轴与D，则
△POD的面积 。
9．已知反比例函数
与一次函数
的图象的一个交点的纵坐标是－4，则
。函数
的自变量的取值范围是
。
10．一次函数的图象与反比例函数
的图象交于A、B两点，A（－2，1），B（1，n），则①反比例函数和一次函数的解析式分别为
，
；②根据图象写出使一次函数的值大雨反比例函数的值的的取值范围是
。
11．请写出“命题：线段垂直平分线上的点到此线段的两端点的距离相等 ”的逆命题
。
二、选择:3×10
1．在函数
的图象上有三点A1（
），A、2（
），A3（
），已知
，则下列各式中，正确的是··················································································································· （ ）
（A）
（B）
（C）
（D）
2．一个矩形的面积是6，则这个矩形的一组邻边长与的函数关系的图象大致是·· （ ）
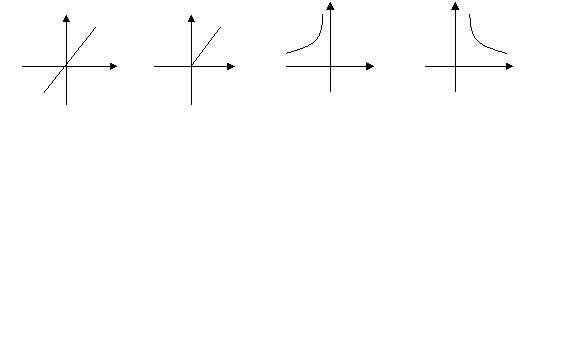
（A） （B） （C） （D）
3．已知反比例函数
，当＜0时，随的增大而增大，那么一次函数
的图象经过 （ ）
（A）第一、二、三象限 （B）第一、二、四象限
（C）第一、三、四象限 （D）第二、三、四象限
4．已知线段a、c（a＜c），求作：Rt△ABC，使∠C=90°，BC=a，AB＝c。作法是①以B为圆心，c为半径作弧，交CM于点A；②连结AB；③作线段BC＝a；④过点C作CM^BC，垂足为C，作法的合理顺序为·· （ ）
（A）①②③④ （B）④③②① （C）③①④② （D）③④①②
5．命题：①对顶角相等；②同角的余角相等；③同一平面内，垂直于同一直线的两条直线平行；④两边和一角对应相等的两个三角形全等。其中假命题的个数········································································· （ ）
（A）1个 （B）2个 （C）3个 （D）4个
6．下列各条件中，不能唯一作出直角三角形的是····················································· （ ）
（A）已知两条直角边 （B）已知两个锐角（C）已知一锐角及其邻边（D）已知一锐角及其对边
7．下列各句中，是命题的是····················································································· （ ）
（A）作∠A的平分线AM （B）垂线段最长
（C）延长线段AB到C （D）两条直线相交于一点吗？
8．已知：如图1，点G是BC的中点，点H在AF上，动点P以每秒2cm的速度沿图1的边线运动，运动途径为：G
CDEFH，相应的△ABP的面积（cm2）关于运动时间t（s）的函数图象如图2，若AB＝6cm，则下列四个结论中正确的个数有······························································································ （ ）
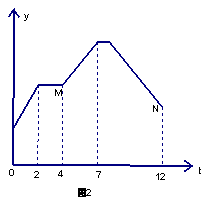
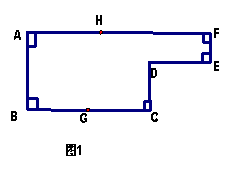①图1中的BC=8cm；②图2中的M点表示第4秒时的值为24cm2；③图1中的CD= 4cm；
④图2中的N点表示第12秒是的值为 18cm2。
（A） 1个 （B） 2个 （C）
3个
（D）4个
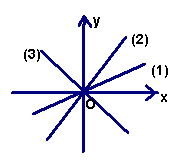
9．如图，三个正比例函数的图象分别对应的关系式是：（1）
；（2）
；（3）
，则
的大小关系是 （ ）
（A）
（B）
（C）
（D）
10．将直线
向左平移两个单位，所得直线方程为··········································· （ ）
（A）
（B） 
（C） 
（D）
三、尺规作图题：4×2＝8分
1．已知线段a，b，c，d，求作梯形ABCD，使得AB∥CD，且AB＝a，BC＝b，CD＝c，DA=d。
（保留痕迹，不需写出作法）
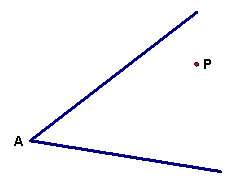
2．已知∠A及∠A内一点P，分别在∠A的两边上作出点B，C，使得△PBC的周长最短。
 |
四、解答题：
1．两条直线l1：y=ax+b和l2：y=cx+5，学生甲解出它们的交点是（3，-2），学生乙因把c抄错而解出它们的交点是（
），试写出这两条直线的解析式. 4分
2．已知一次函数的图象经过点A（0，1）和点B（a，－3a），a＜0，且点B在反比例函数
的图象上。
（1）求a的值； （2分）
（2）求一次函数的解析式，并画出它的图象；（3分）
（3）利用函数的图象，求当这个一次函数y的值在－1≤y≤3范围内相应的x的取值范围（2分） ；
（4）如果P（m，y1）,Q(m＋1，y2)是这个一次函数图象上的两点，试比较y1 与y2的大小（1分）
姓名
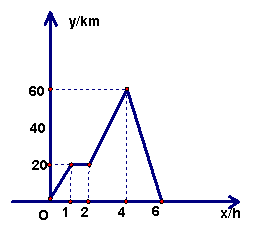
3．小张骑车往返于甲、乙两地，距甲地的路程（km）与时间（h）的函数图象如图所示。
①小张在路上停留 h，他从乙地返回时骑车的速度为 km/h。 （2分）
②小李与小张同时从甲地出发，按相同路线匀速前往乙地，到乙地停止。途中小李与小张共相遇3次。请在图中画出小李距甲地的路程（km）与时间（h）的函数的大致图象。（2分）
③小王与小张同时出发，按相同路线前往乙地，距甲地的路程（km）与时间（h）的函数关系式为
。小王与小张在途中共相遇几次？请你计算第一次相遇的时间。（3次）
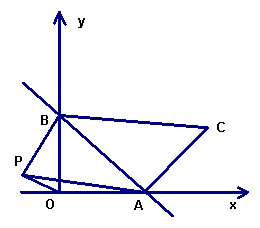
4．如图，直线
与轴、轴分别交于点A、B，以线段AB为直角边在第一象限内作等腰直角三角形△ABC，∠BAC＝90°，如果在第二象限内有一点P（a，
），且△ABP的面积与△ABC的面积相等，求a的值。
（7分）
 |