中学初二数学检测2007-3-18班级 姓名
一、填空题(每空2分，共36分)
1、
的平方根是__________，-8的立方根是
。
2、在实数范围内分解因式：
=____________。
3、化简：
，若a＜-6，则
。
4、式子
有意义，则x的取值范围是
。
5、如果
，则x的取值范围是
。
6、已知x，y为实数，
，则x+y=
。
7、观察下列各式，再完成化简：
，
，… …
，
你能写出一个相同类型的化简题吗？请写出并化简： 。
8、已知直角三角形中两条边的长分别是6cm和8cm，则第三条边长为 。
9、已知等腰梯形的上、下底边的长分别为6cm和16cm，腰长13cm，则它的面积是 。
10、Rt△ABC中∠C=90°，若a=8，b=6，则sinB= ；若b=25，c=30，则cotA= 。
11、含有30°角的直角三角形三边长的比是 ；
含有45°角的直角三角形三边长的比是 。
12、已知梯形的两底边长分别是3cm、5cm，同一底边上两个角分别是30°、60°，则这个梯形的周长是 ，面积是 。
二、选择题(每题2分，共20分)
1、计算
的结果是（ ）
（A）
（B）
（C）1 （D）-1
2、下列各式属于最简二次根式的是（ ）
（A）
（B）
（C）
（D）
3、若
与
是最简同类二次根式，则-b的值是（ ）
（A）0 （B）1 （C）-1 （D）
4、把
根号外的因式移到根号内，结果化简为（ ）
（A）
（B）
（C）
（D） 
5、满足
的整数对（x，y）的个数是（ ）
（A） 1个 （B）2个 （C）3个 （D）多于3个
6、在△ABC中，A、B都是锐角，且sinA=
，cosB=
，则此三角形是（ ）
(A)锐角三角形 (B)直角三角形 (C)钝角三角形 (D)不能确定形状
7、野外生存训练中，第一小组从营地出发向北偏东60o方向前进了3千米，第二小组向南偏东30o方向前进了3千米，经观察、联系，第一小组准备向第二小组靠拢，则行走方向和距离分别为( )
（A）北偏东15°，
千米 （B）南偏西15°， 千米
（C）南偏西15°，3 千米 （D）南偏西45°， 千米
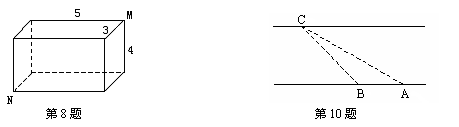
8、设长方体的长、宽、高分别是5分米、3分米、4分米，在长方体表面上从点M到点N处的最短的途径是( )。
（A）
分米 （B）10分米 （C）
分米（D）
分米
9、在△ABC中∠A、∠B是锐角，等式acosB+bcosA=c成立的条件是( )
(A)∠C是锐角 (B)∠C是直角 (C)∠C是钝角 (D)上述三种情形都可以
10、在河岸边一点A测得与对岸河边一棵树C的视线与河岸的夹角为30°、沿河岸前行100米到点B，测得与C的视线与河岸的夹角为45°，则河的宽度为( )
（A）200米 （B）
米 （C）
（D）
 |
三、计算题(各小题3分，共12分)
（1）
（2）
（3） sin60°-4cot30°+3tan30° （4） 已知a是锐角，且cosa=
，
求sina，tana，cota。
四、化简求值(4分)
，其中
，
；
五、解答题(第4题8分，其余每题5分，共28分)
1、已知：
，且x为偶数，求
。
2、已知
，求
的值。
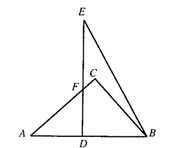
3、将两块三角板如图放置，其中∠C=∠EDB=90°，∠A=45°，∠E=30°，AB=DE=6，
求重叠部分四边形DBCF的面积。
4、（1）判断下列各式是否成立？你认为成立的，在括号内打“√”，否则打“×”。
① 
（ ）
② 
（ ）
③ 
（ ）
④ 
（ ）
（2）你判断完以上各题后发现了什么规律？请用含有n的式子将规律表示出来，并写出n的取值范围。
（3）请你用所学数学知识说明你所写式子的正确性。
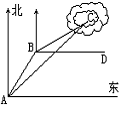
5、一艘渔船在A处观测到东北方向有一小岛C，已知小岛C周围4.8海里范围内是水产养殖场。渔船沿北偏东30°方向航行10海里到达B处，在B处测得小岛C在北偏东60°方向，这时渔船改变航线向正东（即BD）方向航行，这艘渔船是否有进入养殖场的危险？
 |