《三角形》复习题 姓名
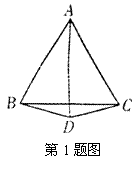1.如图，已知∠ABD=∠BDA=∠ADC=∠DCA=750。请你写出由已知条件能够推出的四个有关线段关系的正确结论（注意：不添加任何字母和辅助线，线段关系仅限于垂直、相等）①________________；②________________；
③________________；④________________.
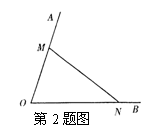
2.已知：M、N分别在∠AOB的边OA、OB上。
求作：以MN为底边的等腰△MNP，使点P在∠AOB的平分线OC上。（要求：用尺规作图，保留作图痕迹，不必写作法和证明）
3.在△ABC中，若AB=AC，若过其中一个顶点的一条直线，将△ABC分成两个等腰三角形，求△ABC个内角的度数（只要求求出三个不同的解）.
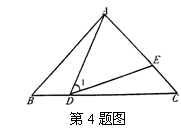4.如图，在△ABC中，AB=AC，D、E分别在BC、AC边上，且∠1=∠B，AD=DE.
求证：△ADB≌△DEC
5．已知等腰三角形一边的长为3，另一边的为5，那么它的周长是 （ ）
A、8 B、11 C、13 D、11或13
6．已知：如图，在△ABC中，AB＝AC。
（1） 按照下列要求画出图形：①作∠BAC的平分线交BC于点D；②过D作DE⊥AB，垂足为点E；③过D作DF⊥AC，垂足为点F。
（2） 根据上面所画的图形，求证：EB＝FC。
7.用反证法证明：“三角形中必有一个内角不小于60°”，应先假设这个三角形中（ ）
（A） 有一个内角小于60°（B）每一个内角都小于60°
（B） 有一个内角大于60°（D）每一个内角都大于60°
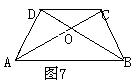
8.如图7，已知AB∥CD,AD=BC,AC、BD相交于点O.求证:OD=OC
9.已知：如图，∠ACB＝∠DBC，要使ΔABC≌ΔDCB，只需增加的一个条件是＿＿＿（只需填写一个你认为适合的条件）
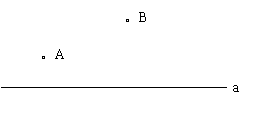10.如图，A、B是两个蓄水池，都在河流a的同旁，为了方便灌溉作物，要在河边建一个抽水站，将河水送到A、B两池，问该站建在河边哪一点，可使所修的渠道最短，试在图中画出该点（不写作法，但要保留作图痕迹）
11．(02宁波)已知：如图，AB⊥BC，AD⊥DC，垂足分别为B、D，AC平分∠BCD.求证：BC＝DC．
12.三角形三内角的度数之比为1：2：3，最大边的长是8㎝，则最小边的长是 ㎝.
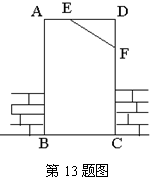
13.如图，工人师傅砌门时，常用木条EF固定矩形门框ABCD，使其不变形，这种做法的根据是
.
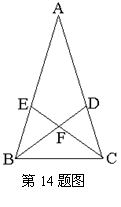
14.如图，在
中，AB=AC，
BD,CE分别为
和
的角平分线，且相交于点F，则图中等腰三角形有 个.请证明其中的一个为等腰三角形.
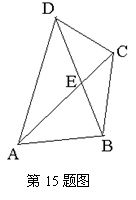15.如图，AC与BD相交于点E，若AC平分
，且AB=AE，AD=AC,有如下四个结论：①AC⊥BD；②BC=DE; ③
;④
是正三角形，请写出正确结论的序号
（你认为正确结论的序号都填上），并选择其中一个正确结论进行证明.
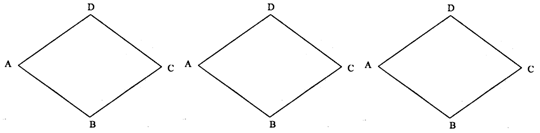
16．已知：如图，图形ABCD中，AB∥CD，AD∥BC，AD=AB，∠A＝72°，请设计三种不同的分法，将图形ABCD分割成四个三角形，使得每个三角形都是等腰三角形．（画图工具不限，要求画出分割线段；标出能够说明分法所得三角形内角的度数；不要求写出画法，不要求证明．）
注：两种分法只要有一条分割线段位置不同，就认为是两种不同的分法．
分法一： 分法二： 分法三：
17.如图,在△ABC中,P,Q分别是BC,AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R,S,若AQ=PQ,PR=PS,下面三个结论: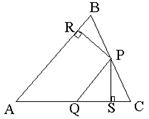 
（1）AS=AR，（2）QP∥AR（3）△BRP≌△CSP正确的是 .
A．(1)和(2) B．(2)和(3) C．(1)和(3) D．(1) 、(2)和(3)
并证明你的结论.
18.已知：如图，点A、E、F、D在同一条直线上，AE＝DF，BF⊥AD，CE⊥AD，垂足为F、E，BF＝CE.求证：AB＝DC.
19.如图，已知△ABC，其中AB＝AC，（1）作AB的垂直平分线DE，交AB于点D，交AC于点E；连结BE.(尺规作图，不写作法，保留作图痕迹)。（2）在（1）的基础上，若AB＝8，△BCE的周长为14，求BC的长. 
20．下列平面图形中，是轴对称图形的有 个.请别作出他们的对称轴.
21.角形一边长为4，一边长9，它的周长是 .
22.求证：等腰三角形底边的中点到两腰的距离相等。（要求完成图形，写出已知。求证，并加以证明）
23.已知：如图，AD是△ABC的角平分线，DE∥AC交AB于点E，DF∥AB交AC于点F.求证：AD⊥EF.
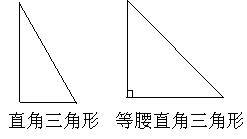
24、试比较下面两个几何图形的异同，请分别写出它们的两个相同点和两个不同点。例如：相同点：直角三角形的内角和为180°，等腰直角三角形的内角和也为180°等。不同点：
等腰直角三角形是轴对称图形，直角三角形不是中心对称图形等.
相同点：（1）
（2）
不同点：（1）
（2）
25. 如图，是一个长方形的门窗，在装修房屋时，为了把它设计成美观大方的图案，设计师要求在长方形形中设计若干个全等的三角形，使其面积的和等于长方形的面积。请你按要求在长方形形中画出你的设计图形（至少三种）.
26.在平面内，分别用3根、5根、6根……火柴首尾依次相接，能搭成什么形状三角形？通过尝试，列表如右所示：
问（1）4根火柴能搭成三角形吗？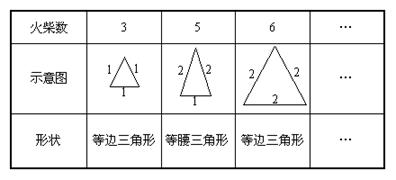
（2）8根、12根火柴能搭成几种不同形状三角形？并画出它们的示意图.
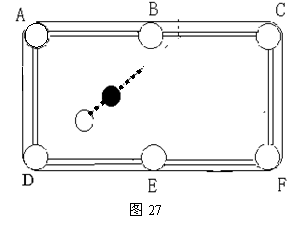27.如图27所示：打台球时，用白球沿着虚线方向击打黑球，已知入射角等于反射角，试问黑球经过一次反弹后是否会进入F号洞？请利用尺规作图来判断（保留画图痕迹，不必证明）.
答： .
22、已知等腰三角形一腰上的中线将三角形的周长分成9㎝和15㎝两部分，求这个三角形腰长和底边的长。
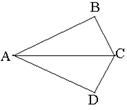
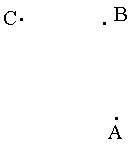
23、如图，点A（乡镇）、B（村）、C（村）同处一片平坦的地区，计划经过点A修筑一条水泥直路l，使点B、C到l的距离相等，在图中画出直线l（用虚线表示能说明画图过程的有关线条）
24、在Rt△ABC中，∠C＝90°，a=3,b＝4,则c= ,斜边上的高线长为
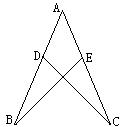25.如图，点D在AB上，点E在AC上，BE和CD相交于点O，AB=AC，∠B=∠C，求证：AD=AE.
26.如图，点C为线段AB延长线上一点，ΔAMC, △BNC是等边三角形，且在线段AB的同侧，求证：AN=MB
27.在△ABC与△A/B/C/中，∠A=∠A/，CD和C/D/分别为AB边和A/B/边上的中线，再从以下三个条件：①AB=A/B/； ②AC=A/C/； ③CD=C/D/中任取两个为题设，另一个为结论，则可以构成3个命题。这三个命题是否正确？若正确，请证明；若不正确，请举反例说明.