华师新版数学八年级第一学期期末测试卷
(时间:120分钟 满分:100分)
一、精心选一选(每题3分,共18分)
1.下面的说法不正确的是( )
A.火车在笔直的铁轨上行驶,可看作火车在平移
B.小明第一次乘观光电梯,随着电梯的上升,他高兴地对同伴说:太棒了,我现在比大楼还高呢,我长高了
C.推开屋门回到温暖的家,离不开旋转变换
D.小明把自己的左手手印和右手手印按在同一张白纸上,左手手印不能通过平移或旋转与右手手印完全重合
2.下列图形中,既是轴对称图形又是中心对称图形的是( )
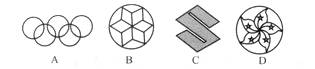
3.在四边形ABCD中,AD∥BC,AC=BD,则四边形ABCD是( )
A.平行四边形 B.等腰梯形 C.矩形 D.等腰梯形或矩形
4.在下列实数中,无理数是( )
A.5 B.0 C. 
D. 
5.
可以写成( )
A.
+ B.·
C.
·
D.
6.如图所示,等腰梯形ABCD中,AB∥DC,AD=BC=8,AB=10,CD=6,则梯形ABCD的面积是( )
A.
B.
C.
D.
二、细心填一填(每题3分,共27分)
7.计算: 
=__________.
8.如果
、
两个实数满足
,则
的立方根是____________.
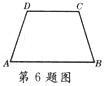
9.如图所示,□ABCD中的全等三角形是___________________.
10.如果2
、、1-这三个实数在数轴上所对应的点从左到右依次排列,那么的取值范围是_____________.
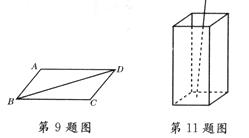
11.如图所示,将一根25cm长的细木棒放入长、宽、高分别为8cm、6cm和
cm的长方体无盖盒子中,则细木棒露在外面的最短长度是___________cm.
12.已知菱形ABCD中,若它的面积是12,且AC=3,则BD=__________.
13.用两个全等的三角形最多能拼成________个不同的平行四边形.
14.如图所示,在周长为30cm的梯形ABCD中,AB∥CD,若DE∥BC,CD=5cm,则ΔADE的周长为__________.
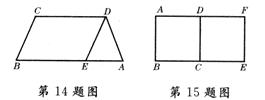
15.如图所示,四边形CDEF旋转后与正方形ABCD重合,那么旋转中心可以取的位置有_____个.
三、用心解一解(共55分)
16.(4分)计算:(x+1)(x+2).
17.(4分)分解因式:
18.(4分)已知:长方体的体积为
cm3,它的长为
cm,宽为
cm.
求:(1)它的高;(2)它的表面积.
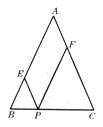
19.(4分)小明和小东经常在一块等腰三角形的草坪上玩耍,一天他们发现了一个有趣的现象:如图,草坪为等腰三角形ABC,AB=AC,他们两人同在BC边上一点P,然后小明沿AC平行线PE(点E在AB上)、EA走向A处,小东沿BA的平行线PF(F点在AC上)、FA走向A处,当他们两个步行速度一样时,则同时到达A点.并且在BC边上不断改变P点位置,在步行速度一定时,他们到达A处的时间也完全一样,你知道为什么吗?说说你的理由.
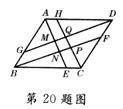
20.(5分)如图,在平行四边形ABCD中,AE、BF、CH、DG分别为四个内角的平分线,这四条角平分线分别交于点M、N、P、Q.
试问:四边形MNPQ是什么四边形?并说明理由.
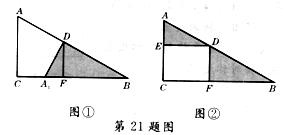
21(6分)观察图①和图②,请回答下列问题:
(1) 请简述由图①变换为图②的形成过程;
(2) 若AD=3,DB=4,求ΔADE与ΔBDF面积的和.
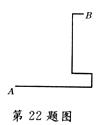
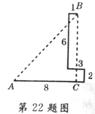
22.(6分)假期中,小明和小强到某海岛观光旅游,在岛上两人参加探宝游戏,按照旅游公司提供的探宝图(如图),它们登陆后先往东走8千米,又往北走2千米,遇到障碍后又往西走3千米,再折向北走6千米往东一拐,仅走1千米就找到了宝藏.问:登陆点A到宝藏老于埋藏点B的直线距离是多少千米?
23.(7分)自我设计:
通 知
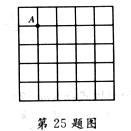
学校有一块正方形空地(见图),要在上面修建一个花园,现征集花园设计方案,要求:在布局上必须体现出旋转的特点,既美观又大方简练,既要是旋转对称图形,又要是轴对称图形......
团委
2007年1月5日
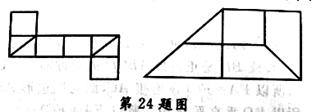
24.(7分)你会把下图分成四个全等的图形吗?试一试.(保留你画的痕迹)
25.(8分)如图,在5×5的正方形网格中,每个小正方形的边长都为1.请在所给网格中按下列要求画出图形.
⑴从点A出发的一条线段AB,使它的另一个端点落在格点(即小正方形的顶点)上,且长度为
;
⑵以⑴中的AB为边的一个等腰三角形ABC,使点C在格点上,且另两边的长都是无理数;
⑶以⑴中的AB为边的两个凸多边形,使它们都是中心对称图形且不全等,其顶点都在格点上,各边长都是无理数.
参考答案:
一.精心选一选
1～6.BBDCDA.
二.细心填一填
7.-72
;8.2;9.ΔABD≌ΔCDB;10.m<0;11.5;12.8;13.3;14.20;15.3;
三.用心解一解
16.
;17.
;18.⑴
(cm);⑵
(cm2);
19.因为PE∥AC,PF∥AB,所以四边形PEAF是平行四边形.所以PE=AF,PF=AE.所以PE+AE=PF+AF.即小明和小东从点P到点A的距距离相等.因此他们在步行速度一定时,到达A处的时间也完全一样.
20.四边形MNPQ是矩形.因为四边形ABCD是平行四边形,所以AD∥BC.所以∠BAD+∠ABC=180O.因为AE、BF平分∠BAD和∠ABC,所以∠BAE+∠ABF=90O,所以∠ANB=180O-(∠BAE+∠ABF)=90O,所以∠MNP=180O -∠ANB=90O.同理可得∠NPQ=∠MQP=90O,所以四边形MNPQ是矩形.
21.⑴图①变换为图②的形成过程是ΔDA1F绕点D顺时针方向旋转90O.
⑵根据旋转的特征,可得AD=A1D=3,∠A1DF=∠ADE.所以∠A1DB=90O.
所以
22.根据题意,构造如图所示的直角三角形,根据勾股定理可得到:登陆点A到宝藏埋藏点B的直线距离是10千米.
23.只要设计的图案体现出旋转的特点,既是旋转对称图形,又是轴对称图形就行.(图略)
24.把图形分成四个全等的图形的情况如图所示:
25.⑴线段AB如图①所示.
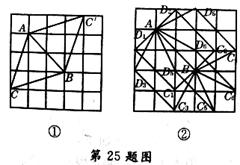
⑵符合要求的等腰三角形有两个,只需画出图①中的两个三角形中的一个即可;
⑶本题答案不惟一,只要画出图②中不全等的两个四边形即可.