反比例函数单元检测

反比例函数单元检测

　　　　　　　　　　　　　　　 2006-4

班别：　　 座号：　 　姓名：　　　 分数：　　　　

一、　　　　 填空题：

1.反比例函数y=的图象经过点(-2,-1),那么k的值为_________。

2.如果点(a,-2a)在函数y=的图象上,那么k______0 (填“>”或“<”)。

3．已知反比例函数，当时，其图象分布在第二、四象限内；当时，其图象在每个象限内随的增大而减小。

4．已知P（1，m+1）在双曲线上，则双曲线在第 　　　　  象限，在每个象限y随x的增大而________。

5．若点A(-2,y₁)、B(-1, y₂)、C(1, y₃)在反比例函数y=的图象上，则、、的大小关系：　　　　　　　　　　　　　　 。

6．式子是　　　　   函数，它的k的值是 　　　　　。

7．已知反比例函数y=(k≠0)与一次函数y = x 的图象有交点, 则k 的范围是____　 __。

二、　　　　 选择题

1．若变量与成正比例，变量又与z成反比例，则与的关系是（　 ） 。

A．成反比例　 B．成正比例　C．y与成正比例  D．与成反比例

2. 若函数y=(m-1)是反比例函数,则m的值等于(　 )。

A.±1　 　　 B.1 　　　　　C.　　　　　　 D.-1

3．一次函数与反比例函数的图象交点的个数为（　　　 ）。

A．0个　　　　B.1个　　　　　  C.2个　　　　　  D.无数个

4．如果P（a，b）在的图象上，则在此图象上的点还有（  ）。

A．（-a，b） 　　B．（a，-b）　 C．（-a，-b） 　D．（0，0）

5．已知函数，又对应的函数值分别是，若， 则有（　　）。

A．y₁>y₂>0　　　 B．y₂>y₁>0　　　 C．y₁<y₂<0　　　D．y₂<y₁<0

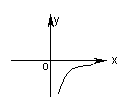6.下列函数中,图象大致为如图的是(　)。

A. y=　 x<0)　　 B. y= (x>0)　

C. y= - (x>0)　  D. y= - (x<0)　

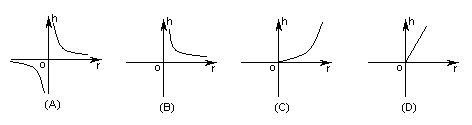
7．已知圆柱体的侧面积为80cm²,若圆柱底面半径为r(cm),高线长为h(cm),则h关于r的函数的图象大致是(　 )。

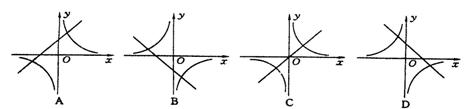
8．若，则函数与在同一平面直角坐标系的图象大致是（　　）。

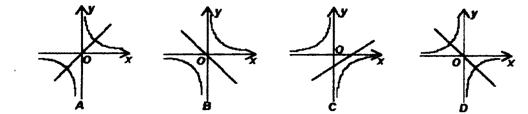
9．函数y=a(x-3)与在同一坐标系中的大致图象是（　　 ）。

10．一次函数y＝kx-2,y随x的增大而减小，那么反比例系数y＝(　　)。

A.当x＞0时，y＞0　　　　 B.在每个象限内，y随x的增大而减小

C.图像在第一、三象限　　　D.图像在第二、四象限

三、填写下面的表格：

函数解析式	k值	图象分布在什么象限	y随x的增大而如何变化	图象可能经过的点
y＝		二、四		（ 3，-2）
y=－2x+4				（　 ，0）
y＝			y随x的增大而增大

四、解答题：

1．已知变量与成反比例，当时，.

求(1) y与x之间的函数关系式;  (2)当 时，的值.

2．码头工人以每天50吨的速度从一艘轮船上卸货，把货物卸完刚好用了10天时间。

（1）轮船到达目的地后开始卸货，卸货的速度v（单位：吨/天）与卸货时间t（单位：天）之间有什么的函数关系？

（2）由于遇到紧急情况，船上的货物必须在不超过5天内卸载完毕，那么平均每天要卸货多少吨？

3．已知反比例函数的图像与一次函数y=kx+m的图像相交于点A（2，1）.

（1）分别求出这两个函数的解析式；

（2）当x取什么范围时，反比例函数值大于0；

（3）若一次函数与反比例函数另一交点为B，且纵坐标为-4，当x取什么范围时，反比例函数值大于一次函数的值；

4．已知反比例函数的图像与一次函数的图像相交于点A（4，-1）、B（-2，m）

（1）求m的值？

（2）分别求出这两个函数的解析式？

（3）如果将一次函数平移后与原来的反比例函数相交与点C（2，-2），那么平移后的一次函数解析式？