说明 ：Ⅰ卷／Ⅱ卷分开制卷
初三毕业考试数学试题（卷）
Ⅰ卷 （请将选择题的答案写在Ⅱ卷的答题卡上）
一 选择题.（每小题３分，共３０分）
1.下列各式计算正确的是（ ）
Ａ． 
Ｂ．
Ｃ． 
Ｄ．
2. 我国“杂交稻之父”袁隆平主持研究的某种超级杂交稻平均亩产820千克。某地今年计划栽插这种超级杂交水稻3000亩，预计今年收获这种杂交水稻的总产量（用科学记数法表示）是 （ ）
A、
B、
C、
D、
3．下列图案是几种名车的标志，在这几个图案中，是轴对称图形的有（ ）
Ａ．1个 Ｂ．2个 Ｃ．3个 Ｄ．4个
4.用两个完全相同的三角形不能拼成下列图形的是 （ ）
A、平行四边形 B、矩形 C、等腰三角形 D、梯形
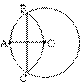5. 如图，⊙O的半径
以A为圆心，OA的长为
半径画弧，交⊙O于B、C，则BC是 （ ）
A、
B、
C、
D、
6．已知点A（2，0）、点B（－
，0）、点C（0，1），以A、B、C三点为顶点画平行四边形．则第四个顶点不可能在（
）
A．第一象限 B．第三象限 C．第二象限 D．第四象限
7．直角三角形中一锐角的正切值为
，周长为24，则斜边长为（ ）
A 10 B 14 C 12 D 15
8. 如图，在
中，
（ ）
A、4 B、5 C、6 D、7
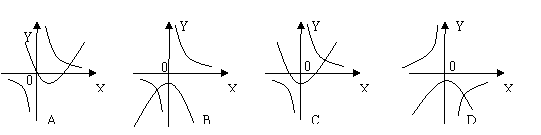9. 函数
在同一坐标系中的图像可能是 （ ）
10.如图，在以O为圆心的两个同心圆中，大圆
的弦AB交小圆于C、D已知AB = 4，CD = 2，
AB 的弦心距等于1，那么两个同心圆的半径之
比（ ）
A 3 ：2 B 
：2 C ：
D 5 ：4
Ⅰ卷 选择题答题卡
| 题号 | １ | ２ | ３ | ４ | ５ | ６ | ７ | ８ | ９ | １０ |
| 选项 |
Ⅱ卷
二．填空题。（每小题４分，共２４分）
11. 某人沿坡度为
的山坡向上走了30米，这时他升高了________米。
12. 冬天某日上海最低气温是
℃，北京最低气温是
℃。这一天，上海的最低气温比北京的最低气温高 ℃
13. 平面镜里看到背后墙上的电子钟示数如图所示，
这时的实际时间是
14. 一次函数y =（m-1）x – m的图像不经过第一象限，则m的取值范围是
15.已知：在⊙O中，弦AB=8cm，弦心距为3cm，则⊙O的半径是
16．梯形ABCD四个顶点都在直径是20cm的⊙O上，其中AB∥CD，AB = 12cm，CD = 16cm， 则梯形ABCD的面积为
三．解答题。
17. （本小题６分）先化简，再求值：
18. （本小题７分）有两组卡片，第一组三张卡片上都写着A、B、B，第二组五张卡片上都写着A、B、B、D、E。试用列表法求出从每组卡片中各抽取一张，两张都是B的概率。
１９． （本小题７分） 有一群猴子，一天结伴去偷桃子，在分桃子时，如果每个猴子分了3个，那么还剩59个；如果每一个猴子分5个，就都能分得桃子，但剩下一个猴子分得的桃子不够5个，你能求出有几只猴子，几个桃子吗？
20. （本小题７分）已知函数：
和
⑴ 在所给的坐标系中画出这两个函数的图像；⑵ 求这两个函数图像的交点坐标；⑶ 观察图像，当
在什么范围时，
？
21. （本小题７分） 求满足下列条件的二次函数解析式：过
两点，与
轴交点的纵坐标为 －2
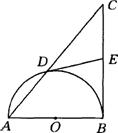
22. （本小题１０分）如图，以Rt△ABC的直角边AB为直径的半圆O，与斜边AC交于D，E是BC边上的中点，连结DE.
(1)DE与半圆O相切吗？若相切，请给出证明；若不相切，请说明理由；
(2)若AD、AB的长是方程x2－10x+24=0的两个根，求直角边BC的长。
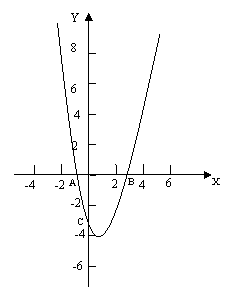
23．（本小题１０分）在直角坐标平面中，O为坐标原点，二次函数
的图象与y轴的负半轴相交于点C（如图5），点C的坐标为（0，－3），且BO＝CO
（1） 求这个二次函数的解析式；
（2） 设这个二次函数的图象的顶点为M，求AM的长.
24. （本小题１２分） 阅读下列材料并填空。平面上有n个点（n≥2）且任意三个点不在同一条直线上，过这些点作直线，一共能作出多少条不同的直线？
（1）分析：当仅有两个点时，可连成1条直线；当有3个点时，可连成3条直线；当有4个点时，可连成6条直线；当有5个点时，可连成10条直线……
（2）归纳：考察点的个数和可连成直线的条数
发现：如下表
| 点的个数 | 可作出直线条数 |
| 2 | 1= |
| 3 | 3= |
| 4 | 6= |
| 5 | 10= |
| …… | …… |
| n |
|
(3)推理：平面上有n个点，两点确定一条直线。取第一个点A有n种取法，取第二个点B有（n－1）种取法，所以一共可连成n(n-1)条直线，但AB与BA是同一条直线，故应除以2；即
（4）结论：
试探究以下几个问题：平面上有n个点（n≥3），任意三个点不在同一条直线上，过任意三个点作三角形，一共能作出多少不同的三角形？
（1）分析：
当仅有3个点时，可作出 个三角形；
当仅有4个点时，可作出 个三角形；
当仅有5个点时，可作出 个三角形；
……
（2）归纳：考察点的个数n和可作出的三角形的个数，发现：（填下表）
| 点的个数 | 可连成三角形个数 |
| 3 | |
| 4 | |
| 5 | |
| …… | |
| n |
(3)推理：
（４）结论：