初中二年级上学期期末考试卷

初中二年级上学期期末考试卷

一、填空题：（每空2分，共28分）

1．直线y＝－2x－1与x轴的交点坐标为_______，与y轴的交点坐标为_______.

2. 直线y＝－3x＋5过第_______象限，y随x的增大而_______.

3． 若正比例函数y＝（m－1）x^︳m︱-3的图像经过第二、四象限，则m的值是________.

4．已知等腰三角形的周长为10cm，将底边长y（cm）表示成腰长x（cm）的函数关系式是______________________，自变量x的取值范围是_______.

5．已知y－1与x+3成正比例，且x＝2时，y＝10，则y与x的函数关系式为_______.

6.请你写出一个以为解的二元一次方程组______________________.

7.已知方程组中，x，y的值相等，则a ＝ ________.

8．已知不等式组无解，则m的取值范围是_______.

9．已知一次函数y = kx+b,当x减少9时，y反而增大3，则k＝ ________.

10．当x________时，函数y＝－2x+5的函数值大于－1.

二、选择题：（每题3分，共30分）

11．下列四个图像（如图）中，不表示某一函数的是　　　　　　　　 （　　 ）

 　　 　

　　　  A　　　　　　　 B　　　　　　　　　 C　　　　　　　　 D

12.函数y＝ +  中，自变量x的取值范围是　　 　　　　（　　 ）

 A.x≠1　　　　 B.x≥　　　　 C.x≥且x≠1　　　D. x≥或x≠1

13．点A（－5，y₁）和B（－2，y₂）都在直线y＝－x上，则y₁与y₂的关系是（　　 ）

A. y₁≤y₂　　　 B.y₁＝y₂　　　　 C.y₁＜y₂　　　　　  D.y₁＞y₂

14．甲.乙两人练习跑步，，如果甲让乙先跑10米，甲跑5秒钟后就可追上乙，如果甲让乙先跑2秒钟，那么甲跑4秒钟就能追上乙，若设甲、乙每秒钟跑x、y米，列出方程组为　　　　　　　　　　　　　　　　　　　　　  （　　 ）

A．　　　　　　　　　 B.

C．　　　　　　　　  D.

15．不等式组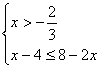的最小整数解为　　　　　　　　　　　  （　　 ）

A.-1　　　　　　 B.0　　　　　　 C.1　　　　　　  D.4

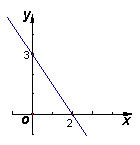
16. 一次函数的图像如右图所示，当y＞0时，

x的取值范围是　　　　　　　　　　　　　　　　　　　　　　　 （　　 ）　　　　　　　　　　　　　　　　　　　　　　　

A.x＞2　　　　　 B.x＜2　　　　

　C.x＞3　　　　　 D. x＜3

17．如果一次函数当自变量x的取值范围是-1＜x＜3时，函数y值的范围是－2＜y＜6，那么此函数的解析式为　　　　　　　　　　　　　　　　　 （　　 ）

A．y＝2x　　B. y＝－2x+4　 C.y＝2x或y＝－2x+4　 D.y＝－2x或y＝2x-4

18．若b≠0，且y＝ax＋b 的图像不过第四象限，则点（a，－b）所在象限为　 （　　 ）

A．一　　　　　 B.二　　　　　　 C.三　　　　　　 D.四

19．将直线y＝5x－平移后过点（－1，－），则平移后直线的解析式为（　　 ）

A．y＝5x＋5　　B.y＝5x－5　　　　C.y＝5x－　　  D. y＝5x＋

三、解答题：（19题8分，20、21题各10分，共28分）

20.解方程组：　　　　21.解不等式组：－3≤＜1

22．画出一次函数y＝x－2 的图像，由图像回答下列问题：

　 （1）求x取何值时，y＝0？

　 （2）当－1＜x＜1时，求y的取值范围.

　 （3）当－2≤y≤－1时，求x的取值范围.

　 （4）在－2≤x≤5范围，求y的最大值和最小值.　

23.正比例函数与一次函数的图像的交点A的坐标为（4，3）； B(0, －3)为一次函数与y轴的交点.

　 （1）求两个函数的解析式.

　 （2）求三角形AOB的面积. 

 

24.在某校初一年级四个班的200名学生中，有部分学生在校住宿，在安排宿舍时，若每间住6人，则有5人住不下；若每间住8人，则有两间寝室没人住，问宿舍共有几间？

25. 某服装厂生产一种西装和领带，西装每套定价200元，领带每条定价40元，厂方在开展促销活动期间，向客户提供两种优惠方案.

（1）买一套西装送一条领带.

（2）西装和领带都按定价90％付款.

某商店老板要到该服装厂购买西装20套，领带x（x＞20）条，问：（1）根据x的不同情况选择这两种方案中哪种方案比较优惠？ （2）此外，你还能找到更省钱的购买方案吗？（写出方案即可）

试卷答案如下：

一、填空题：（每空3分，共27分）

1、（－，0）;(0, -1)　　　　  2.一、二、四；减小　　　　 3、－4　　

4、y＝10－2x ；2.5cm﹤x﹤5cm　　 5、y＝x＋　　 6、答案不唯一　　

7、16　　　　　  8、m≥2　　　　　  9、－　　　　　　　 10、＜3

二、选择题：（每题3分，共21分）

11、D　 12、C　 13、D　 14、D　　15、B　 16、B　 17、C　18、D　 19、D

三、解答题：（19题8分，20、21题各10分，共28分）

20、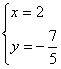　　　　　　　　　　　  21、0＜x≤

22、图略；（1）求x＝3时，y＝0；

　　　　 （2）当－1＜x＜1时，－2＜y＜－1；

　　　　 （3）当－2≤y≤－1时，0≤x≤1.5；

　　　　 （4）在－2≤x≤5时，y_大＝，y_小＝－ .

23、解：

（1）由图像设正比例函数解析式为y＝kx + b （k≠0）

又∵过点A（4，3），

　　 ∴3＝4k，∴k＝，∴y＝x

设一次函数解析式为y＝kx + b（k≠0），

　　 ∴　 　　　　　∴　

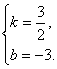
　　 ∴y＝x－3

（2）S_△AOB＝＝OB×︳x_A︳=×3×4=6

24、 11或12或13或14间 

　　 设有宿舍x间，根据题意得x－3＜≤x－2，解得10.5≤x≤14.

25、（1）设购买第一种需用y₁元，购买第二种需用y₂元，

则y₁＝200×20＋（x－20）×40＝40x＋3200，

y₂＝（200×20＋40x）×90％＝36x＋3600

㈠当40x＋3200﹥36x+3600,即：

当x﹥100时用第二种方案省钱.

㈡当x＝100时，两种相同.

㈢当x﹤100时，第一种方案省钱.

（2）方案③若同时选择两种方案，为了能获得厂方赠送领带的数量最多，又同时享受9折优惠，先按方案①购买20套西装并获增20条领带，然后余下（x－20）条领带按优惠方案②购买.