初二数学科期末考试卷
一、选择题（每小题3分，共24分）
1．10名学生的体重分别是41、48、50、53、49、50、53、62、51、67（单位：kg）这组数据的极差是 （ ）
A．27 B．26 C．25 D．24
2．若△ABC中，AB=13，AC=15，高AD=12，则BC的长是 （ ）
A．14 B．4 C．14或4 D．以上都不对
3．在式子
中，分式的个数是
（ ）
A．2 B．3 C．4 D．5
4．下列函数中，y是x的反比例函数的是 （ ）
A．
B．
C．
D．y=2x+1
5．已知y与x成正比例，z与y成反比例，那么z与x之间的关系是 （ ）
A．成正比例 B．成反比例
C．有可能成正比例，也有可能是反比例 D．无法确定
6．下列命题正确的是 （ ）
A．对角线互相平分的四边形是菱形
B．对角线互相平分且相等的四边形是菱形
C．对角线互相垂直的四边形是菱形
D．对角线互相垂直且平分的四边形是菱形
7．如下图，某花木场有一块等腰梯形ABCD的空地，其各边的中点分别是E、F、G、H，测得对角线AC=10米，现想用篱笆围成四边形EFGH场地，则需篱笆总长度是 （ ）
A．40米 B．30米 C．20米 D．10米
 |
8．某班50名学生身高测量结果如下表：
| 身高 | 1.51 | 1.52 | 1.53 | 1.54 | 1.55 | 1.56 | 1.57 | 1.58 | 1.59 | 1.60 | 1.62 |
| 人数 | 1 | 1 | 3 | 4 | 3 | 4 | 4 | 6 | 8 | 10 | 6 |
该班学生身高的众数和中位数分别是 （ ）
A．1.60和1.56 B．1.59和1.58 C．1.60和1.58 D．1.60和.60
二、填空题（每空2分，共28分）
1．当x、y满足关系
时，分式
有意义。
2．直线y=kx+b过一、三、四象限，则函数
的图象在
象限，并且在每一个象限内y随x的增大而
。
3．已知一个直角三角形的两条直角边分别为6cm、8cm，那么这个直角三角形斜边上的高为 。
4．已知正比例函数y=kx与反比例函数
图象都过A（m,1），则m= ，正比例函数的解析式是
。
 |
5．如图，正方形ABCD的周长为16cm，顺次连结正方形ABCD各边的中点，得到四边形EFGH，则四边形EFGH的周长等于 cm，四边形EFGH的面积等于 cm2
6．如图，在平行四边形ABCD中，AE垂直于CB的延长线于E，AF⊥CD，交CD的延长线于点F，若∠EAF=135o,BC=6cm，AB=8cm，则∠C= 度，AF= cm，
AE= cm，□ABCD的面积为 cm2。
7．为了调查某一路段的汽车流量，记录了30天中每天同一时段通过该路口的汽车辆数，其中有4天284辆，4天是290辆，12天是312辆，10天是314辆，那么这30天该路口同一时段通过的汽车平均数为 。
8．某次射击练习中，甲、乙二人各射靶5次，命中的环数如下表：
| 甲射靶环数 | 7 | 8 | 6 | 8 | 6 |
| 乙射靶环数 | 9 | 5 | 6 | 7 | 8 |
那么射击成绩比较稳定的是 。
三、计算题（每小题8分，共24分）
1．化简：
2．解方程：
3．如图，Rt△ABO的顶点A是双曲线
与直线
在第二象限的交点，AB⊥x轴于B且S△ABO=。
（1）求这两个函数的解析式；
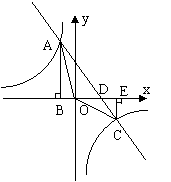（2）若A（-1，3），C（3，-1），求△AOC的面积。
四、证明题（第1题10分，第2题12分，共22分）
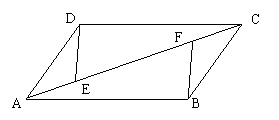
1．已知：如图，在平行四边形ABCD中，E、F是对角线AC上的两点，且AE=CF
求证：DE=BF
 |
2．求证：三角形的中位线平行于三角形的第三边，且等于第三边的一半。
五．解答题（第1题10分，第2题12分，共22分）
1．小明向西南方向走40米后，又走了50米，再走30米回到原地，小明又走了50米后向哪个方向走的？
2．某市举行一次少年滑冰比赛，各年龄组的参赛人数如下表所示：
| 年龄组（岁） | 13 | 14 | 15 | 16 |
| 参赛人数 | 5 | 19 | 12 | 14 |
（1）求全体参赛选手年龄的众数，中位数。（6分）
（2）小明说，他所在年龄组的参赛人数占全体参赛人数的28%，你认为小明是哪个年龄组的选手？请说明理由。（6分）