初二数学期中复习试卷（四）
出卷：洪澄 审核：初二数学备课组 班级_________姓名_______
一填空:
(1)81的平方根是____ 
的算术平方根是 ，0.001的立方根是
(2) 大于
且小于
的所有整数是_____ 比较大小
______ 
。
(3)计算
＝ ；
＝_______；
___
(4) （2x + y）（2x — y）=___________；（2a —1）2= ___________;
____
(5)如图，小红欲横渡一条河，由于水流的影响，实际上岸地点C偏离欲到达点B200m，结果他在水中实际游了520m，则该河流的宽度为 。
(6) 若直角三角形的三边a、b、c满足a2－4a+4+
=0,则笫三边c的长度是_______．
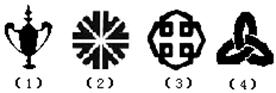
(7)在右边四个图形中是轴对称图形的是 ，是旋转对称图形的是 ，是中心对称图形的是 。（填序号）
(8) 如图，P是正三角形 ABC 内的一点，且PA＝6，PB＝8，PC＝10．若将△PAC绕点A逆时针旋转后，得到△P'AB ，则
点P与点P' 之间的距离为_______，∠APB＝______°
(9) 如图，长方体长、宽、高分别为4cm、3cm、12cm，则
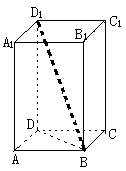BD1＝
cm。
(10)
=_____,
=___
=____;……．通过以上计算,试用含n(n为正整数)的式子表示上面运算揭示的规律:________．
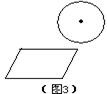
(11) 如图3，请你画一条直线，同时把两个图形分成形状、大小都相同的两部分。
二、选择题
(1)下列说法正确的是（ ）
A.
的平方根是±9
B.
＝±2 C.1的平方根是1 D.
的算术平方根是2
(2) 树顶落在离树干底部
处，则这棵树在折断前（不包括树根）长度是（ ）A. B.
C.
D.
(3)
能成为完全平方式
A、
B、
C、
D、以上都不对
(4) 用一副扑克牌做实验，选其中的黑桃5和方块4，是中心对称图形是 ( )
A.黑桃5 B.方块4 C.黑桃5和方块4 D.以上都不对
(5)一直角三角形的一条直角边长是7cm，另一条直角边与斜边长的和是49cm，则斜边的长( )A、18cm B、20cm C、24cm D、25cm
(6)2002年8月在北京召开的国际数学大会会标取材于我国古代数学家赵爽的《勾股圆方图》，它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形（如图）。如果大正方形的面积是13，小正方形的面积是1，直角三角形较短直角边为a，较长直角边为b，那么（a+b）2的值为（ ）A、13 B、19 C、25 D、169
三、解答题
（1）－12x3y4÷(－3x2y3)·(－
xy). （2）用乘法公式计算14
×15.
（3）(x－2)2(x+2)2·(x2+4)2. （4）[（x-y）2—（x + y）2]÷（—4xy）
（5）(3x+2)(x－1)=3(x－1)(x+1).
（6）若
，求
的值．
 |
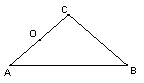（7）在等腰直角△ABC中，∠C=90°，BC=2cm，如果以
AC的中点O为旋转中心，将这个三角形旋转180°，点B落
在点B′处，求BB′的长度.
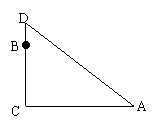（8）在一棵树的10米高处有两只猴子，一只猴子爬下树走到离树20米处的池塘的A处。另一只爬到树顶D后直接跃到A处，距离以直线计算，如果两只猴子所经过的距离相等，则这棵树高多少米？
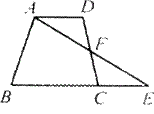
（9）如图，四边形ABCD中，AD∥BC，DF=CF，连结AF并延长交BC延长线于点E.（1）图中哪两个三角形可以通过怎样的旋转而相互得到？（2）四边形ABCD的面积与图中哪个三角形的面积相等？
（3）若AB=AD＋BC，∠B=70°，试求∠DAF的度数.
宜兴市升溪中学初二数学期中复习试卷（八）
出卷：洪澄 审核：初二数学备课组 班级_________姓名_______
一、填空
1、–125的立方根是_____ ，9的算术平方根是 。
的平方根是
2、如果
，那么
要使
有意义，则x可以取的最小整数是
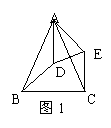3、
；(______)
；3a2 — a（a —1）=________。
4、如图1，△ABC、△ADE均是顶角为400的等腰三角形，BC、DE分别是底边。图中△ACE可看作是由△ABC以点A为旋转中心，逆时针旋转 ________度而得到的。
5、一艘帆船由于风向的原因先向正东方向航行了160km，然后向正北方向航行了120km，这时它离出发点有____________km.
6、在△ABC中，AB＝5，BC＝12，AC＝13，则AC边上的高是
7、将△ABC平移至△DEF,若A与D，B与E，C与F是对应点，AB=6cm,AD=10cm则DE= BE= 。
8、木工周师傅做一个长方形桌面，测量得到桌面的长为60cm，宽为32cm，对角线为68cm，这个桌面 (填”合格”或”不合格”)。
9、如果
那么a2-b2＿＿＿;若
则 
＿＿＿
10、等腰直角三角形ABC中，∠C＝90°，BC=2cm,如果以AC的中点O为旋转中心，将这个三角形顺时针方向旋转180°，点B落在点B′处，那么线段BB′=
cm；
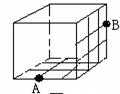
11、所示一棱长为3cm的正方体，把所有的面均分成3
3个小正方形。其边长都为1cm，假设一只蚂蚁每秒爬行2cm，则它从下底面点A沿表面爬行至侧面的B点，最少要用 秒钟；
二、选择
1、⊿ABC中，如果三边满足关系
=
+
，则⊿ABC的直角是（ ）A ∠
C B ∠A C ∠B D 不能确定
2、．如果
，
，则
的值是（
）
（A）2 （B）1 （C）－2 （D）－1
3、下列说法正确的是（ ）A、无限小数都是无理数 B、无理数都是无限小数
C、带根号的数都是无理数
D、两个无理数的和还是无理数
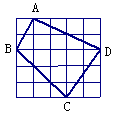
4、如图小方格都是边长为1的正方形,则四边形ABCD的面积是（ ）
A. 25 B. 12.5 C. 9 D. 8.5
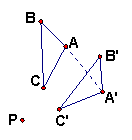
5、如图，⊿
是由⊿ABC绕点P通过旋转得到的，若线段
长度为
，点A在旋转过程中所经过的路程为
，则、的大小关系为（ ）A、＜ B、＞ C、＝ D、、的大小关系不确定
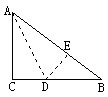
6、如图，有一块直角三角形纸片，两直角边AC=6cm,BC=8cm,现将直角
边AC沿直线AD折叠，使它落在斜边AB上，且与AE重合，则CD等于（ ）
A. 2㎝ B. 3㎝ C. 4㎝ D. 5㎝
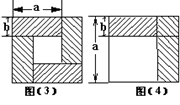7、我们已经接触了很多代数恒等式，知道可以用一些硬纸片拼成的图形面积来解释一些代数恒等式。例如图（3）可以用来解释（a+b）2－（a－b）2=4ab。那么通过图（4）面积的计算，验证了一个恒等式，此等式是（ ）
A、a2－b2=（a+b）（a－b） B、（a－b）（a+2b）=a2+ab－b2
C、（a+b）2=a2+2ab+b2 D、（a－b）2=a2－2ab+b2
三、解答题
（1）
（2）
（3）
（4）[(x-y)2-(x+y)(x-y)]÷(-2y) （5） 98×102－992
（6）化简求值(2x＋1)2－9(x＋2)(x－2)＋5(x＋1)(x－3)其中x=－2
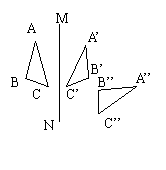
（7）如图，△ABC和△A’B’C’关于直线MN对称，△A’B’C’和△A’’B’’C’’
关于直线EF对称。(1)画出直线EF；(2)直线MN与EF相交于点O，
试探究∠BOB’’ 与直线MN、EF所夹锐角α的数量关系。
（8）如图，要在河边修建一个水泵站，分别向张村A和李庄B送水，已知张村A、李庄B到河边的距离分别为2km和7km，且张、李二村庄相距13km．
（1）水泵应建在什么地方，可使所用的水管最短？请在图中设计出水泵站的位置；
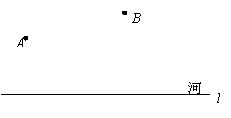（2）如果铺设水管的工程费用为每千米1500元，为使铺设水管费用最节省，请求出最节省的铺设水管的费用为多少元？