初二数学期中练习题
北京市立新学校
 A类要求:
A类要求:
一、 选择题:
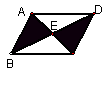
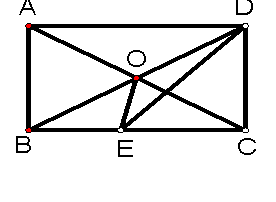
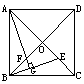
1.如图,E为平行四边形ABCD内一点,若S□ABCD=6,
则图中阴影部分的面积为( ).
A.2 B.3 C.4 D.5
2.如图,在方格纸中有四个图形①、②、③、④,其中面积相等的图形是( )
A.①和② B.②和③ C.②和④ D.①和④
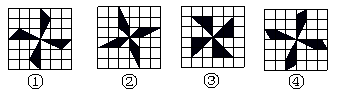
3.在下面图形中,每个大正方形网格都是由边长为1的小正方形组成,则图中阴影部分面积最大的是( )
① ② ③ ④
 4.已知菱形的边长为6cm,一个内角为60度,则菱形较短的对角线长是( )
4.已知菱形的边长为6cm,一个内角为60度,则菱形较短的对角线长是( )
A.6cm B.3cm C.12cm D.9cm
5.已知:如图,在矩形ABCD中,E,F,G,H分别为边AB,BC,CD,DA
的中点.若AB=2,AD=4,则图中阴影部分的面积为( )
A.3 B.4 C.6 D.8
6.矩形具有而一般平行四边形不具有的性质是( )
A.对角线互相平分 B.邻角互补 C.对角相等 D.对角线相等
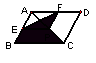 7.如图,四边形ABCD中,P为AC对角线上一点,PE∥BC交
7.如图,四边形ABCD中,P为AC对角线上一点,PE∥BC交
AB于点E,PF∥AB交AD于点F.若S=20(cm2), 则图中阴影部分
的面积= (cm2).
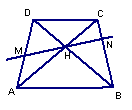
8.如图,已知直线m∥n,A、B为直线n上的两点,C、P为直线上m的两点,
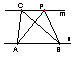 (1) 请写出图中面积相等的各对三角形:
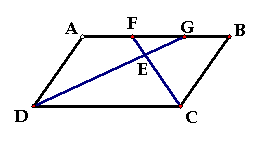
(1) 请写出图中面积相等的各对三角形:
(2) 若A、B、C为三个定点,点P在直线m上移动,
无论P点移动到任何位置,总有与ΔABC的面积相等,
理由是 .
9.若平行四边形的两邻边长分别为16和20,两长边距离为8,则两短边距离为 .
10.矩形ABCD中,对角线AC,BD相交于点O,∠BOC=2∠AOB.若AC=18cm,则
AB= cm.
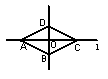 11.已知,平行四边形ABCD的对角线AC和BD交于点O,若△AOB的面积是3,那么平行四边形ABCD的面积是 .
11.已知,平行四边形ABCD的对角线AC和BD交于点O,若△AOB的面积是3,那么平行四边形ABCD的面积是 .
12.如图,直线l是四边形ABCD的对称轴,若AB=CD,有下面的
结论①AB∥CD;②AC⊥BD;③OA=OC;④AB⊥BC.
其中正确的结论有: .
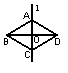 13.如图,l是四边形ABCD的对称轴,如果AD∥BC,有下列结论:
13.如图,l是四边形ABCD的对称轴,如果AD∥BC,有下列结论:
①AB∥CD,②AB=BC,③AB⊥BC,④AO=OC.其中正确的
结论是 .(把你认为正确的结论的序号都填上)
14.写出一条菱形特有而一般平行四边形没有的特性(性质): .
24.菱形具有而矩形不一定具有的特性是 .(写出一条就行)
 15.已知:如图,在矩形
ABCD 中,等腰直角△EFC 内接于矩形.
15.已知:如图,在矩形
ABCD 中,等腰直角△EFC 内接于矩形.
若 ED = 2,矩形周长为 16,则 AE = _ ___.
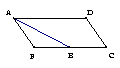 16.如图,在平行四边形ABCD中,AD=5,AB=8,AE平分∠BAD
16.如图,在平行四边形ABCD中,AD=5,AB=8,AE平分∠BAD
交CD于E,求EC的长.
17.(1)如图,AD是△ABC的角平分线,DE∥AC交AB于E,DF∥AB交
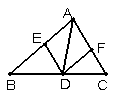 AC于F,试说明四边形AEDF是菱形.
AC于F,试说明四边形AEDF是菱形.
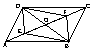 18.如图,在平行四边形ABCD中,对角线AC与BD交于O点,已知点
18.如图,在平行四边形ABCD中,对角线AC与BD交于O点,已知点
E、F分别是AO、OC的中点,试说明四边形BFDE是平行四边形.
B类要求:
 19.如图,面积为12(cm^2)的△ABC沿BC方向平移至△DEF的位置,平移的距离是BC长的两倍,则图中的四边形ABED的面积为( )
19.如图,面积为12(cm^2)的△ABC沿BC方向平移至△DEF的位置,平移的距离是BC长的两倍,则图中的四边形ABED的面积为( )
A.24(cm2) B.36(cm2) C.48(cm2 ) D.无法确定
 20.如图,把一个长方形纸片沿EF折叠后, 点D、C分别
20.如图,把一个长方形纸片沿EF折叠后, 点D、C分别
落在D'、C'的位置,若∠EFB=65度,∠AED'等于( )。
A.50度 B.55度 C.60度 D.65度
21.菱形的周长为a,高为h,一条对角线为m,则另一条对角线的长是( )
(A)ah
(B)hm
(C)am (D)![]()
 22.如图,平行四边形ABCD中,过点A作直线交BC于点E,交DC的
22.如图,平行四边形ABCD中,过点A作直线交BC于点E,交DC的
延长线于点F,若△ABF的面积为5,则△ADE的面积为 .
23.平行四边形ABCD的周长为28,它的对角线AC和BD交于点O,且△AOB的周长比△BOC的周长大2,那么AB的长是 .
24.若一个平行四边形一个内角的平分线把一条边分成2和3两条线段,则该平行四边形的周长是 或 .
25.如图,将矩形ABCD的对角线BD对折,对折后BC、AD的交点为E,将重叠部分剪下并展开,则四边形BE'DE的形状是 ,理由是 .
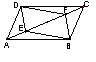 26.如图,点E、F是平行四边形ABCD对角线AC上两点,
请你添加
26.如图,点E、F是平行四边形ABCD对角线AC上两点,
请你添加
一个适当的条件: ,四边形DEBF是平行四边形.
27.已知平行四边形ABCD,试用两种方法将平行四边形ABCD分成面积相等的四个部分.
0.
 28.如图,矩形ABCD中,对角线AC、BD交于点O,DE平分
28.如图,矩形ABCD中,对角线AC、BD交于点O,DE平分
∠ADC交BC于点E,∠BDE=15°,
求(1)∠COD的度数;(2)∠COE的度数.
 29.如图,平行四边形ABCD,∠BCD的平分线CF交 边AB于F,
29.如图,平行四边形ABCD,∠BCD的平分线CF交 边AB于F,
∠ADC的平分线DG交边AB于G.
(1)求证:AF=GB
(2)请你在已知条件的基础上再添加一个条件,使得△EF为等腰直角三角形,并说明理由.

30.如图,在平行四边形ABCD中,AB=2BC,M为AB的中点,
试说明CM⊥DM.
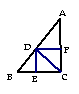 |
31.如图,△ABC中,∠C=90度,CD平分∠ACB,过点D
分别作DE⊥BC,DF⊥AC,垂足分别为E,F,试说明:四边形
DECF是正方形.
32.如图,在△ABC中,D为BC边上的一动点? (点D不与B、
C两点重合).DE∥AC交AB于E点,DF∥AB交AC于F点.?
⑴试探索AD满足什么条件时,四边形AEDF为菱形,并加以说明;
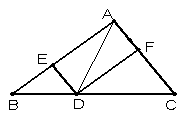 ⑵在⑴条件下,△ABC满足什么条件时,四边形AEDF为正方形.
⑵在⑴条件下,△ABC满足什么条件时,四边形AEDF为正方形.
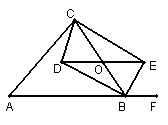 33.如图,在△ABC中,O为BC上一点,过O作直线OE∥AB交∠ABC,
33.如图,在△ABC中,O为BC上一点,过O作直线OE∥AB交∠ABC,
∠CBF的平分线于点D,E,连结CD,CE,
(1)说明DO=OE;
(2)当点O在BC的什么位置时,四边形为矩形?
(3)在(2)的条件下,△ABC又满足什么条件时,四边形BDCE为正方形?
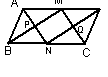
34.如图,M、N分别是平行四边形ABCD的对边AD、
BC的中点,且AD=2AB,说明:四边形PMQN为矩形.
 |
35.如图,ABCD中AQ、BN、CN、DQ分别是∠DAB、∠ABC、∠BCD、
∠CDA的平分线,AQ、BN交于点P,CN、DQ交于点M,求证:MP=NQ.
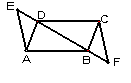 36.如图,在平行四边形ABCD中,E、F是直线BD上两点,
36.如图,在平行四边形ABCD中,E、F是直线BD上两点,
且DE=BF,试说明AE=CF.
37.如图,已知△ABC中,AB=AC,E是AB的中点, D在BC上.延长
 ED到F,使ED=DF=EB.连结FC.说明四边形AEFC是平行四边形.
ED到F,使ED=DF=EB.连结FC.说明四边形AEFC是平行四边形.
38.如图,在平行四边形ABCD中,点E、F在对角线AC上,
 且AE=CF,观察图形,以图中标明字母的点为端点添加线段,
且AE=CF,观察图形,以图中标明字母的点为端点添加线段,
请你猜想出一个与你添加的线段有关的正确结论.
39.如图,把边长为2的正方形剪成四个形状相同,大小相等的直角三角形。请用这四个直角三角形拼成符合下列要求的图形(全部用上,互不重叠且不留空隙),并把你的拼法仿照图中实际大小画在方格纸内.?
 ⑴不是正方形的菱形(一个)
⑴不是正方形的菱形(一个)
⑵不是正方形的矩形(一个)
⑶梯形(一个)
⑷不是矩形和菱形的平行四边形(一个)
⑸不是梯形和平行四边形的凸四边形(一个)
40.已知:平行四边形ABCD,在AD、BC所在直线上分别取点E,F,当满足下列条件时,怎样画线段EF?
⑴AC、EF互相平分
⑵AC、EF互相平分且AC=EF
⑶AC、EF互相平分且AC⊥EF
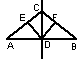
41.如图,点D是线段AB的中点,点C是线段AB的垂直
平分线上的任意一点,DE⊥AC于点E,DF⊥BC于点F.
⑴求证:CE=CF;
⑵点C运动到什么位置时,四边形CEDF成为正方形?请说明理由.
C类要求:
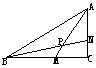
42.点P是边长为1的菱形ABCD对角线AC上一个动点,
点M、N分别为AB,BC边上的中点,MP+NP的最小值是( )
A.2 B.1 C.(3/2) D.(1/2)
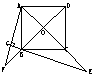
43.如图,点E是平行四边形ABCD的一边延长线上一点,
 DE交BC于F,求证:S△ABF=S△EFC.
DE交BC于F,求证:S△ABF=S△EFC.
 44.如图,平行四边形ABCD中,对角线AC=21cm,
BE⊥AC,垂足为E,
44.如图,平行四边形ABCD中,对角线AC=21cm,
BE⊥AC,垂足为E,
且BE=5cm,AD=7cm,试求AD和BC之间的距离.
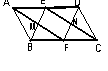 45.已知:如图,平行四边形ABCD中,E、F分别为AD、BC中点,
45.已知:如图,平行四边形ABCD中,E、F分别为AD、BC中点,
BE、AF交于M,EC、DF交于N.?
⑴当ABCD的一组邻边满足什么条件时,四边形EMFN是矩形.?
⑵当ABCD的一个内角满足什么条件时,四边形EMFN是菱形.
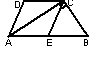 46.已知如图,AB∥CD,AD∥CE,且∠ACB=90度,E是AB的中点.?
46.已知如图,AB∥CD,AD∥CE,且∠ACB=90度,E是AB的中点.?
⑴试说明DE与AC相互垂直平分;
⑵探究:当四边形AECD是正方形时,∠B的度数?
 |
47.如图,已知△ABC中,AB=AC,M是BC的中点,MG⊥AB,
MD⊥AC,GF⊥AC,DE⊥AB,垂足分别为G、D、F、E,GF与
DE相交于H,请你判断四边形HGMD的形状,并说明理由.
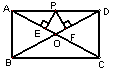
48.如图,在矩形ABCD中,AB=3,AD=4,P是AD上的与A、D
不重合的一动点,PE⊥AC,PF⊥BD,E、F为垂足,求PE+PF的值.
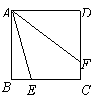
49.已知:如图,E是正方形ABCD中BC上任意一点,AF平分ÐEAD交CD于F.求证:BE+DF=AE.
50.如图,正方形ABCD中对角线AC、BD相交于O,E为AC上一点,AG⊥EB交EB于G,AG交BD于F。
(1)说明OE=OF的道理;
(2)若E为AC延长线上,AG⊥EB交EB的延长线于G,AG、BD的延长线交于F,其他条件不变,如图2,则结论:“OE=OF”还成立吗?请说明理由.
51.如图,在△ABC中,∠C=90°,点M在BC上,且BM=AC,点N在AC上,且AN=MC。AM与BN相交于点P。求证:∠BPM=45°
52.如图,已知AC是□ABCD的对角线,△ACP和△ACQ都是等边三角形,求证:四边形BPDQ是平行四边形.
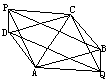
53.如图,以△ABC的三条边为边向BC的同一侧作等边△ABP、等边△ACQ,等边△BCR,求证:四边形PAQR为平行四边形.
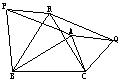
54.如图,两条等宽的长纸条倾斜地重叠着,试证重叠部分ABCD为菱形.
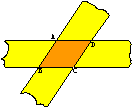
55.如图,△ABC中,∠C=90°,AD平分∠BAC,ED⊥BC于D,DF//AB,求证:AD与EF互相垂直平分。
56.四边形ABCD中,AB=BC=CD=DA,∠BAD=120°,M为BC上的点,若△AMN中有一角等于60°,求证:△AMN为等边三角形.
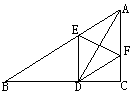
57.如图,△ABC中,∠A=90°, ∠B的平分线交AC于D,AH、DF都垂直BC,垂足为H、F,求证:四边形AEFD为菱形.
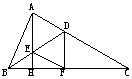
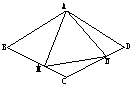
58. △ABC的三条中线分别为AD、BE、CF,H为BC边外一点,且四边形BHCF为平行四边形,求证:AD//EH.
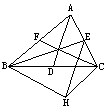
59.如图,点P是等边△ABC内任意一点,过P点分别作各边的平行线,
E、F、M、N、G、H,请猜测线段EF、MN、GH的和是什么?当点P
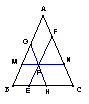 在等边△ABC内运动时,所猜测的结论有变化吗?
在等边△ABC内运动时,所猜测的结论有变化吗?
60.已知:如图,△ABC是等边三角形,过AB边上的点D作
DG∥BC,交AC于点G,在DG的延长线上取点E,使DE=DB,
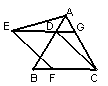 连结AE,CD.
连结AE,CD.
⑴求证:△AGE≌△DAC.
⑵过点E作EF∥DC,交BC于点F,请你连结AF,并判断△AEF是怎样的三角形,试证明你的结论.
61. 以三角形ABC的三边为边,在直线BC的同侧向形外作等边三角形△ABD、△BCE、△ACF.四边形ADEF是平行四边形吗?为什么?
62.如图,分别以AB、AC为边向△ABC形外作正方形ABDE 、
正方形ACGF,M、N、 P、Q分别是EF、BC、EB、FC的中点.
(1)猜想四边形MPNQ的形状:试证明你猜想的结论:
 (2)△ABC形状的改变是否对上述结论有影响,请简要说明.
(2)△ABC形状的改变是否对上述结论有影响,请简要说明.
63. 如图,已知△ABC,分别以AB、AC为边向外作等边△ABF、△ACE,
再以AE、AF为边向外作平行四边形AEDF, 试判断△BCD的形状,
 并证明你的结论.
并证明你的结论.
64. 如图,E为□ABCD外一点,且AE⊥EC,BE⊥ED.
 求证: □ABCD是矩形.
求证: □ABCD是矩形.
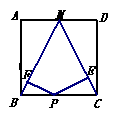 65. 如图,点M是矩形ABCD边AD的中点,点P是BC上一动点,
65. 如图,点M是矩形ABCD边AD的中点,点P是BC上一动点,
PE⊥MC,PF⊥MB,垂足为E、F.
(1) 当矩形ABCD的长与宽满足什么条件时,四边形
PEMF为矩形?
(2) 在(1)中,当点P运动到什么位置时,矩形PEMF边
为正方形,为什么?
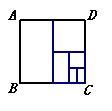 66.如图,把一个面积为1的正方形等分成两个面积为
66.如图,把一个面积为1的正方形等分成两个面积为![]() 的矩形,
的矩形,
接着把面积为![]() 的矩形等分成两个面积为
的矩形等分成两个面积为![]() 的矩形,再把面
的矩形,再把面
积为![]() 的矩形等分成两个面积为
的矩形等分成两个面积为![]() 的矩形,如此进行下去,
的矩形,如此进行下去,
试利用图形揭示的规律计算:![]() = .
= .

67. 如图,已知 □ ABCD中,AE⊥BD,CF⊥BD,垂足为E、F
,G、H分别为AD、BC的中点, 求证:EF和GH互相平分.
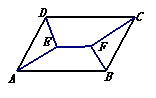 68. 如图, □ABCD中,AB>BC,∠A与∠D的平分线交于点E,
68. 如图, □ABCD中,AB>BC,∠A与∠D的平分线交于点E,
∠B与∠C的平分线交于点F .
(1) EF与AB之间有怎样的位置关系?为什么?
(2) EF、BC与AB之间有怎样的数量关系?为什么?
(3) 如果将条件“AB>BC”改为“AB<BC”,情形有如何呢?
试探索说明.
69. 如图,E为矩形ABCD的边AD上一点,且 BE=DE, P为对角线
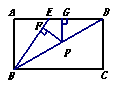 BD上一点,
PF⊥BE于F,PG⊥AD于G.
,求证:PF+PG=AB
BD上一点,
PF⊥BE于F,PG⊥AD于G.
,求证:PF+PG=AB
70.如图,梯形ABCD中,AB∥CD,对角线AC、BD垂直相交于H,
M是AD上的点,MH所在的直线交BC于N,在以上的前提下,
 试将下列设定中的两个作为题设,另一个作为结论组成一个正
试将下列设定中的两个作为题设,另一个作为结论组成一个正
确的命题,并探求这个命题
① AD=BC; ②MN⊥BC; ③AM=DM.
(全等)
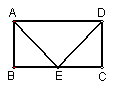 71.已知:如图,平行四边形ABCD中,E
是 BC 中点,AE
= ED,
71.已知:如图,平行四边形ABCD中,E
是 BC 中点,AE
= ED,
求证:四边形 ABCD 是矩形.
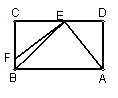 72.已知:如图,在矩形
ABCD 中,BE平分角ABC
交 DC
72.已知:如图,在矩形
ABCD 中,BE平分角ABC
交 DC
于 E,EF⊥AE交 BC 于 F,求证:AE = EF .
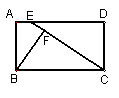 73.已知:如图,在矩形
ABCD 中,点 E 为
AD 上一点,且
73.已知:如图,在矩形
ABCD 中,点 E 为
AD 上一点,且
CE = BC,BF⊥EC,求证:AB = BF .
74.已知:如图,平行四边形ABCD 中,M、N 分别是 CD,
AB 上的点,E、F 是 AC上的点,若CM = AN,AE = CF,
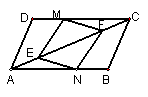 求证:四边形 MENF 是平行四边形.
求证:四边形 MENF 是平行四边形.
75.已知:如图,在矩形 ABCD 中,AC 的中垂线交
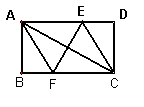 AD 于
E ,交 BC 于
F,求证:四边形AFCE是菱形.
AD 于
E ,交 BC 于
F,求证:四边形AFCE是菱形.
76.如图,矩形ABCD中,AC与BD交于O点,
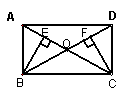 BE⊥AC于E,CF⊥BD于F.求证:BE=CF.
BE⊥AC于E,CF⊥BD于F.求证:BE=CF.
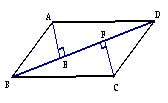 77.如图,平行四边形ABCD中,AE⊥BD,CF⊥BD,
77.如图,平行四边形ABCD中,AE⊥BD,CF⊥BD,
垂足分别为E、F,求证:∠BAE=∠DCF.
平移
1. 下列现象中,属于平移的是: 【 】
⑴温度计中,液柱的上升或下降; ⑵打气筒打气时,活塞的运动;
⑶钟摆的摆动 ; ⑷传送带上,瓶装饮料的移动
A.⑴,⑵ B.⑴,⑶ C.⑵,⑶ D.⑵,⑷
2. 下列现象中,属于平移的是: 【 】
A.空中放飞的风筝 B.飞机在直线跑道上滑行到停止的运动
C.篮球运动员投球进入篮筐的过程 D.乒乓球比赛中的高抛发球后,乒乓球的运动
3. 观察图中的图形,请说出平移的方向和距离.
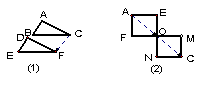
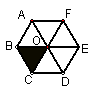 4.如图,O是正六边形ABCDEF的中心,下列图形中可由△OBC平移得到的是( ).
4.如图,O是正六边形ABCDEF的中心,下列图形中可由△OBC平移得到的是( ).
A.△OCD B.△OAB C.△OAF D.△OEF
5.判断:
⑴线段a∥b,则线段b可以看做是线段a平移得到的.( )
⑵线段a=b,则线段b可以看做是线段a平移得到的.?( )
⑶线段b是由线段a平移得到的,则一定有a∥b.? ( )
⑷图形在平移的过程中对应点所连的线段一定平行.( )
6.如图,△ABE沿射线所示方向平移一定距离后成△CDF.
 ⑴图中平行且相等的三条线段是 ;
⑴图中平行且相等的三条线段是 ;
⑵若AB=2cm,则CD= ,
若∠AEB=45O,则∠CFD= .
7.小明把自己的左手和右手手印按在同一张纸上,左手手印(填“能”或“不能”)通过平移与右手手印完全重合.( )
8.如果同一平面的两个图形通过平移,不论其起始位置如何,总能完全重合,则这两个图形是( )
A.两个点 B.两个半径相等的半圆
C.两个点或两个半径相等的半圆 D.两个完全相等的多边形
9.将字母E向上平移4cm的作图中,第一步是在字母“E”上至少需找出关键的 个点.
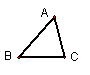 10.将△ABC沿BC方向平移2厘米,画出平移后的图形.
10.将△ABC沿BC方向平移2厘米,画出平移后的图形.
 |
11.如图,经过平移,△ABC的边AB移到了EF,作出平移后的三角形.
12.以线段a=16,b=13,c=10,d=6为边,且使a∥c作四边形,这样的四边形( )
A.能作一个 B.能作两个 C.能作无数个 D.不能作
13. 图形的操作过程(本题中四个矩形的水平方向的边长均为a,竖直方向的边长均为b):
在途中,将线段A1A2向右平移1个单位到B1B2,得到封闭图形A1A2B2B1(即阴影部分);
在图中,将折线A1A2A3向右平移1个单位到B1B2B3得到封闭图形A1A2A3B3B2B1(即
阴影部分).
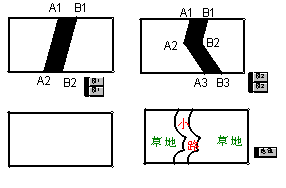 ⑴在图中,请你类似地画一条有两个折点
⑴在图中,请你类似地画一条有两个折点
的线, 同样向右平移1个单位,从而得到一
个封闭图形,并用斜线画出阴影;
⑵请你分别写出上述三个图形中除去阴影
部分后剩余部分的面积;
S1= S2= S3= .
联想与探索:
⑶如图, 在一块矩形草地上,有
一条弯曲的柏油小路(小路任何地方水平宽度都是1个单位),请你猜想空白部分表示的草地面积是多少?并说明你的猜想是正确的.
小明家进行装修的时候,需要一块菱形的木板,但现在手头上只有一块矩形木板,小明想把矩形木板变成菱形木板,又不浪费一点材料,请你想办法通过切割和平移矩形木板,将其变成菱形木板,解决这个难题(画出示意图).
旋转
1.
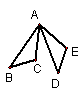 如图,△ABC经过旋转后达到△ADE的位置,∠BAD=55度,在这个旋转过程中:
如图,△ABC经过旋转后达到△ADE的位置,∠BAD=55度,在这个旋转过程中:
⑴旋转的中心是点 ;⑵旋转的角度是 ;
⑶点B的对应点是点 ;⑷∠C的对应角是 ;
⑸线段BC的对应线段是 .
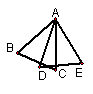 |
2. 如图,三角形ADE是由三角形ABC旋转得到的,通过观察,
旋转中心是点 ,在△ADE中,与∠ACB对应的是 ,
与线段AB对应相等的是线段 .
 |
3. 如图,如果把钟表的指针看作四边形AOBC,它绕O点旋转
得到四边形DOEF,则旋转角的度数与( )的度数相等.?
A.∠AOB B.∠BOD C.∠DOE D.∠AOD
4.
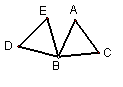 如图,等边△BDE是由等边△BAC经过旋转得到的,试判断旋转
如图,等边△BDE是由等边△BAC经过旋转得到的,试判断旋转
中心和旋转角度以及旋转的方向.
5.
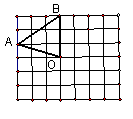
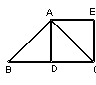 如图,△ABC是等腰直角三角形,点D是斜边BC中点,△ABD
如图,△ABC是等腰直角三角形,点D是斜边BC中点,△ABD
绕点A旋转到△ACE的位置,恰与△ACD组成正方形ADCE,则
△ABD绕点A所作的旋转是( ).
A.顺时针旋转225度 B.逆时针旋转45度
 C.顺时针旋转315度
D.逆时针旋转90度
C.顺时针旋转315度
D.逆时针旋转90度
6.如图,∠BCD=120度,把△BCD绕C点按顺时针方向旋转60度
到△ACE的位置,则BC旋转到了 ,∠ACD=
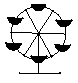 7.如图所示是游乐园中的大型旋转车的简图,游人坐在旋转车的车斗中,
7.如图所示是游乐园中的大型旋转车的简图,游人坐在旋转车的车斗中,
任旋转车不停地旋转,但总是头朝上,绝不会掉下来,试问车斗所作的
移动式什么移动?请在下面答案中选一个正确的确答案( )
A.旋转 B.对称 C.平移 D.以上答案都不对
8.在旋转过程中,下列命题中正确的是:( )
⑴图形上每一点都移动了相同的距离; ⑵图形上每一点都绕旋转中心转过了相同的角度;
⑶对应点到旋转中心的距离相等; ⑷所有的对应点到旋转中心的距离都相等.
A.(1),(2) B.(2),(3) C.(3),(4) D.(2),(4).
9.经过旋转,图形上的每一点都绕旋转中心沿相同的方向转动了相同角度.
A.任意一对对应点与旋转中心的连线所成的角都是旋转角
B.对应点到旋转中心的距离相等
C.旋转中心也转动了相同的角度
 D.经过旋转的图形,有且只有一个与已知点对应
D.经过旋转的图形,有且只有一个与已知点对应
以上错误的选项是( )
10.如图所示,画出△AOB绕O点顺时针旋转90度后的图形,
并指出图中相等的线段和角.
11.小华同学正在黑板上画△ABC绕△ABC外一点P旋转60度角的旋转图,当他完成A、B两点旋转后的对应点A'、B'时,不小心将旋转中心P擦掉了,没有旋转中心P,小华不知道如何继续画下去,请同学们帮助小华找到旋转中心P, 使他继续完成剩下的图形.
 |
12.图中△ABC与△A'B'C'是形状、大小完全一样的两 个三角形,同过平移、旋转使得△ABC运动到△A'B'C'的位置,请同学们动手试一试,看谁的方法多.
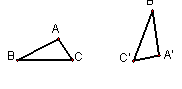 |
13.小亮在镜中看到身后墙上的时钟如图,你认为实际时间最接近8点的是( ).
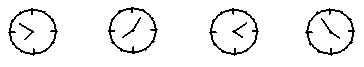
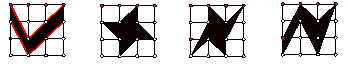
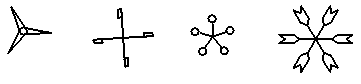
14.观察图中所列“风车”的平面图案,其中既是轴对称图形,又可以通过旋转得到的图形有( )
A.1个 B.2个 C.3个 D.4个
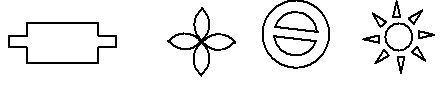
15.可由旋转得到的有( )
A.1个 B.2个 C.3个 D.4个
16.如图所示,把一个直角三角尺ACB绕着30度角的顶
点B顺时针旋转,使得点A与CB的延长线上的点E重合.?
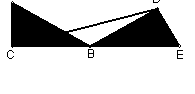
⑴三角尺旋转了多少度?
⑵连结CD,试判断△CBD的形状.?
⑶求∠BDC的度数.