初二 第一学期半期考数学卷
第一学期半期考数学卷
数 学 试 卷
(完卷时间:120 分 满分:100分 命题:林森 审核:林世保)
题 号 | 一 | 二 | 三 | 总 分 | |||||||
17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | ||||
得 分 | |||||||||||
评卷人 | |||||||||||
一、选择题(每小题2分,共20分)
1.下列函数中,是正比例函数的是( )

 A.
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
2.下列图形中与图 全等的图形是( )
A. B. C. D.
 3.期中考后,老师为了清楚地看出数学成绩各个分数段人数在全班总人数中所占的百分比,应采用的统计图是( )
3.期中考后,老师为了清楚地看出数学成绩各个分数段人数在全班总人数中所占的百分比,应采用的统计图是( )
A.条形图 B.扇形图 C.折线图 D.直方图
4.观察统计图,下列结论正确的是( )
A.甲校女生比乙校女生少
B.乙校男生比甲校男生少
C.乙校女生比甲校男生多
D.甲、乙两校女生人数无法比较
 5. 在直角坐标系中,直线
5. 在直角坐标系中,直线![]() 经过点( )
经过点( )
A.(![]() ,
,![]() )
B. (
)
B. (![]() ,
,![]() )
)
C.(![]() ,
,![]() )
D. (
)
D. (![]() ,
,![]() )
)
6. 2005年10月福州市遭受“龙王”台风袭击,闽江
水位上涨.小明以警戒水位为![]() 米,用折线统计图表示某
米,用折线统计图表示某
一天江面水位情况.请你结合折线统计图判断下列叙述不
正确的是( )
A.8时水位最高 B.这一天水位均高于警戒水位
C.8时到16时水位都在下降 D.![]() 点表示12时水位高于警戒水位0.6米
点表示12时水位高于警戒水位0.6米
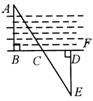 7.要测量河两岸相对的两点A、B间的距离,先在AB的垂线BF上
7.要测量河两岸相对的两点A、B间的距离,先在AB的垂线BF上
取两点C、D,使CD=BC,再定出BF的垂线DE,使A、C、E在一条直
线上,这时测量ED的长就等于A、B间的距离,这是因为△EDC≌△ABC,
全等的根据是( ).
 A. SAS B. ASA C. SSS D. H L
A. SAS B. ASA C. SSS D. H L
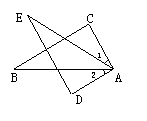
8.如图,已知![]() ,
,![]() ,增加下列条件:
,增加下列条件:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .
.
其中能使![]() 的条件有( )
的条件有( )
A.![]() 个 B.
个 B.![]() 个 C.
个 C.![]() 个 D.
个 D.![]() 个
个
9.函数与自变量满足下表关系的解析式为( ).
|
|
| -1 | 0 | 1 | 2 |
|
|
|
| -5 | -2 | 1 | 4 |
|
![]() .
.![]()
![]() .
.![]()
![]() .
.![]()
![]() .
. ![]()
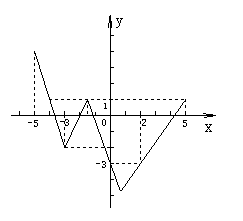
10. 如图,是某函数的图象,则下列结论中正确的是( )
A.当![]() 时,
时,![]() 的取值是
的取值是![]()
B.当![]() 时,
时,![]() 有最大值是1
有最大值是1
C.当![]() 时,函数值
时,函数值![]() 最大
最大
 D.当
D.当![]() 时,
时,![]() 随
随![]() 的增大而增大
的增大而增大
二、填空题(每空3分,共18分)
 11.函数
11.函数![]() 中,自变量
中,自变量![]() 的取值范围是
.
的取值范围是
.
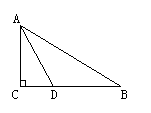
12.如图,在△ABC中,∠C=900,AD平分∠CAB,DC
=8cm,那么D点到直线AB的距离是 cm.
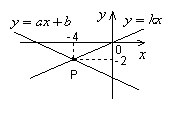
13. 如图,已知函数![]() 和
和![]() 的图象交于点
的图象交于点
 P, 则根据图象可得,关于
P, 则根据图象可得,关于![]() 、
、![]() 的二元一次方程组
的二元一次方程组![]()
的解是
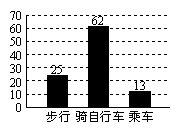
14.某中学为了解学生上学方式,现随机抽取部分学生进
行调查,将结果绘成条形统计图如下,由此可估计该校2400
名学生中有. 名学生是乘车上学的.
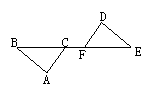 15.如图,已知AB∥DE,AC∥DF,AC=DF,BF=10,
15.如图,已知AB∥DE,AC∥DF,AC=DF,BF=10,
CF= 4,则BE的长为 .
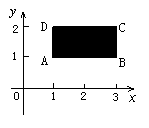 16.如图,有一种动画程序,屏幕上长方形
16.如图,有一种动画程序,屏幕上长方形![]() 是黑色区域
是黑色区域
(含长方形边界),其中![]() ,用信号枪
,用信号枪
沿直线![]() 发射信号,当信号遇到黑色区域时,区域便由
发射信号,当信号遇到黑色区域时,区域便由
黑变白,则能够使黑色区域变白的![]() 的取值范围为
.
的取值范围为
.
三、解答题(共62分)
 17、(4分)如图,要在S区建一个集贸市场P,
17、(4分)如图,要在S区建一个集贸市场P,
使它到公路,铁路距离相等,集贸市场P离
公路与铁路交叉处500米,请在图上标出这
个集贸市场的位置(比例尺为1︰20000).
S
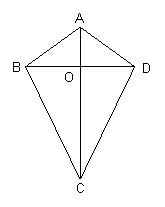 18、(7分)如图,四边形ABCD中,AC垂直BD于点O, O为BD的中点.
18、(7分)如图,四边形ABCD中,AC垂直BD于点O, O为BD的中点.
(1)图中有多少对全等三角形?请把它们都写出来;(3分)
(2)任选(1)中的一对全等三角形加以证明.(4分)
19. (6分)鞋子的“鞋码”和鞋长(cm)存在一种换算关系,下表是几组“鞋码”与鞋长的对应数值:
| 鞋长 | 16 | 19 | 24 | 27 |
| 鞋码 | 22 | 28 | 38 | 44 |
(1)分析上表,“鞋码”与鞋长之间的关系符合你学过的那种函数?(1分)
(2)设鞋长为![]() ,“鞋码”为
,“鞋码”为![]() ,求
,求![]() 与
与![]() 之间的函数关系式;(3分)
之间的函数关系式;(3分)
(3)如果你需要的鞋长为26cm,那么应该买多大码的鞋?(2分)
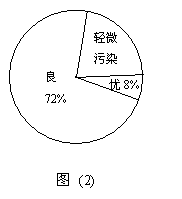
20.(8分)随着人们环保意识的增强,大家对居住环境的空气质量情况日益重视。下图8(1)和8(2)是某校初一年级的环保小组根据全国多个城市的空气质量情况进行了抽样调查后,绘制的两幅不完整的统计图.请你根据图中提供的信息,解答以下问题:
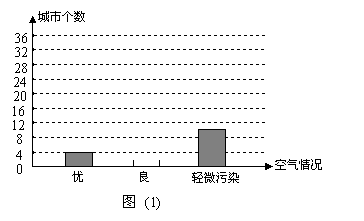 | |||
 | |||
(1)环保小组共抽样调查了 个城市的空气质量情况.(2分)
(2)在 图(1)中将等级为“良”的部分补充完整.(2分)
(3)在 图(2)中,计算等级为“轻微污染”的部分所对应的圆心角度数.(2分)
(4)若以该统计结果去估算全国300个城市的空气质量情况,达到“优秀”等级的城市共有多少个?(2分)
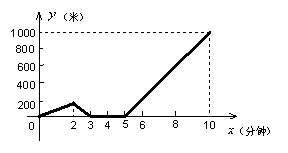 21.(8分)小文家与学校相距1000米.某天小文上学时忘了带一本书,走了一段时间才想起,于是返回家拿书,然后加快速度赶到学校.下图是小文与家的距离
21.(8分)小文家与学校相距1000米.某天小文上学时忘了带一本书,走了一段时间才想起,于是返回家拿书,然后加快速度赶到学校.下图是小文与家的距离![]() (米)关于时间
(米)关于时间![]() (分钟)的函数图象.请你根据图象中给出的信息,解答下列问题:
(分钟)的函数图象.请你根据图象中给出的信息,解答下列问题:
(1)小文走了多远才返回家拿书?(2分)
(2)小文在家呆了多长时间?(2分)
(3)小文这次行程的平均速度是多少?(2分)
(4)当![]() 分钟时,求小文与家的距离?(2分)
分钟时,求小文与家的距离?(2分)
 22. (8分)已知,如图,AB∥CD,∠A =90°,AB=CE,BC=DE.
22. (8分)已知,如图,AB∥CD,∠A =90°,AB=CE,BC=DE.
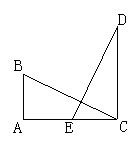 求证:DE⊥BC.
求证:DE⊥BC.
23、(9分)某电视台为某个广告公司特约播放甲、乙两部连续剧.经调查,播放甲连续剧平均每集有收视观众20万人次,播放乙连续剧平均每集有收视观众15万人次,公司要求电视台每周共播放7集.
(1)设一周内甲连续剧播![]() 集,甲、乙两部连续剧的收视观众的人次的总和为
集,甲、乙两部连续剧的收视观众的人次的总和为![]() 万人次,求
万人次,求![]() 关于
关于![]() 的函数关系式;(3分)
的函数关系式;(3分)
(2)已知电视台每周只能为该公司提供不超过300分钟的播放时间,并且播放甲连续剧每集需50分钟,播放乙连续剧每集需35分钟,请你用所学知识求电视台每周应播放甲、乙两部连续剧各多少集,才能使得每周收看甲、乙连续剧的观众的人次总和最大,并求出这个最大值.
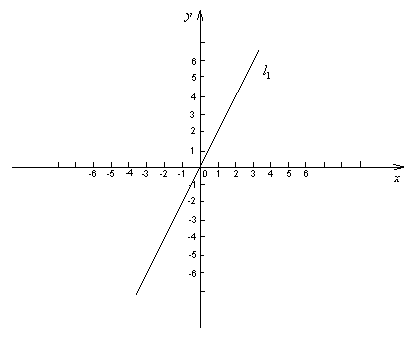
24.(12分)如图,已知:直线![]() 的函数解析式为
的函数解析式为![]() ,直线
,直线![]() 的解析式为
的解析式为![]() ,直线
,直线![]() 与
与![]() 轴相交于
轴相交于![]() ,与
,与![]() 轴相交于
轴相交于![]() ,与直线
,与直线![]() 相交于
相交于![]() ,点
,点![]() ,
,![]() 是
是![]() 轴上的一个动点,过点
轴上的一个动点,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() ,交
,交![]() 于
于![]() ,交
,交![]() 于
于![]() .
.
(1)求点![]() 、
、![]() 的坐标,并画出直线
的坐标,并画出直线![]() ;(3分)
;(3分)
(2)当![]() 时,试用含
时,试用含![]() 的代数式表示
的代数式表示![]() 、
、![]() 、
、![]() 、
、![]() 的长;(4分)
的长;(4分)
 (3)在
(3)在![]() 轴是否存在点
轴是否存在点![]() ,使△
,使△![]() 与△
与△![]() 全等,若存在,直接写出点
全等,若存在,直接写出点![]() 的坐标;若不存在,试说明理由.(5分)
的坐标;若不存在,试说明理由.(5分)