八年级数学下期末复习综合测试题二
姓名_____________ 班级____________ 分数____________
一、选择题（10×3′=30′）
1、下列命题中正确的是（ ）
A、若a<b<0，则不等式ax<b的解集为x< C、相等的角是对顶角
B、一般而言,一组数据的极差、标准差越小,数据就越稳定D、一组数据的众数只有一个
2、已知直角三角形的三边分别为a、a+b、a+2b，其中a>0,b>0,则a与b的比为（ ）
A、1∶3 B、1∶4 C、2∶1 D、3∶1
3、甲、乙两人两次都同时去某个米店买米,甲每次买m（m为正整数）千克米,乙每次用去2m元,由于市场方面的原因,虽然这两次米店出售的是一样的米,但米价却分别为每千克a元,b元,那么比较甲两次买米的平均单价与乙两次买米的平均单价结果是（ ）
A、甲、乙的平均单价B、甲比乙便宜C、乙比甲便宜D、由m、a、b的值确定
4、直角三角形的周长为48,一锐角的平分线分对边为3∶5,则斜边长为（ ）
A、20 B、15 C、25 D、16
5、下列多项式中,能用完全平方公式分解因式的是（ ）
A、x2-x+1 B、1-2xy+x2y2 C、a2+a+ D、-a2+b2-2ab
6、一组数据的方差为S2,平均数为
,将这组数据中的每个数据都乘以2所得到的一组新数据的方差与平均数是（ ）
A、S2, B、S2,
C、2S2,2 D、4S2,2
7、若分式不论x取何值总有意义,则m的取值范围是（ ）
A、m≥1 B、m>1 C、m<1 D、m≤1
 |
8、如果要使关于x的方程
有唯一解,那么需要（ ）
A、m≠1且m≠3 B、m≠3 C、m≠1且m≠2 D、m≠1
9、如图,E为
ABCD的AD边上一点,且AE∶ED=1∶3,F为AB的中点,EF交AC于G,则AG∶GC为（ ） A、1∶2 B、1∶5C、1∶4 D、1∶3
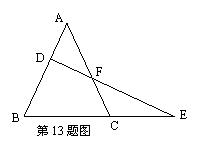
10、如图,将△ADE绕正方形ABCD的顶点A顺时针旋转90°,得△ABF,连接EF交AB于H,则下列结论错误的是（ ）
A、AE⊥AF B、EF∶AF=∶1 C、AF2=FH·FE D、FB∶FC=HB∶EC
二、填空题（10×3′=30′）
11、已知关于x的不等式组
无解,则a的取值范围是___________.
12、若分式的值等式零,,则x=_________________________.
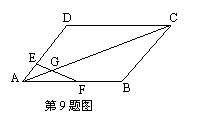
13、如图,D、F分别为△ABC的边AB、AC上的点,且AD∶DB=CF∶FA=2∶3，连DF交BC的延长线于E,则EF∶FD=_________________________.
14、把命题“等底等高的两个三角形面积相等”的条件与结论互换,得新命题为_______________________________，这个命题是___（填“真”或“假”）命题.
15、一个正整数若分别加上100与168,就可得到两个完全平方数，则这个正整数是_______.
16、一次函数y=（3-k）x+k的图象经过第一、二、四象限,则k的取值范围是_____________.
17、甲、乙两比赛射击,两人所得平均环数相同,其中甲所得环数的标准差为4,乙所得环数如下：1，5，0，9，10.那么成绩较稳定的是___________.
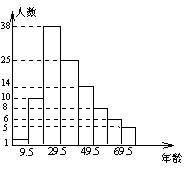18、2003年，国家卫生部信息统计中心根据国务院
新闻办公室授权发布全国内地5月21日至5月25
日非典型肺炎发病情况，按年龄段进行统计分析中，
各年龄段发病的总人数如图所示。观察图形你能获
得哪些信息（至少写三条）：
。
19、已知一个矩形的面积为4a2-2ab+b2，其中一边长
是4a-4，则其周长为_________________________.
20、B地在A地的北偏东60°的30km处,C地在A地的北偏西30°的方向上,∠BCA=30°，直线
表示经过C地并和BC垂直的一条公路,则A地到的距离是_____________________.
三、解答题（共60分）
21、（2×4′=8′）分解因式
（1）4a（b-a）-b2 （2）（p-1）（p2-pq+q2）+pq（1-p）
22、（2×5′=10′）
（1）解不等式组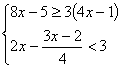
，并把解集在数轴上表示出来.
（2）化简求值:（+）÷ 其中x=-
23、（10′）某零件制造车间有工人20名,已知每名工人每天可制造甲种零件6个或乙种零件5个,且每制造一个甲种零件可获利润150元,每制造一个乙种零件可获利润260元,在这20名工人中,车间每天安排x名工人制造甲种零件,其余工人制造乙种零件.（1）请写出此车间每天利润y（元）与x（人）之间的函数关系式.（2）若要使车间每天所获利润不低于24000元,你认为至少要派多少名工人去制造乙种零件才合适?
24、（10′）某工程由甲、乙两队合做6天完成,厂家需付甲、乙两队共8700元；乙、丙两队10天完成,厂家需付乙、丙两队共9500元；甲、丙两队合做5天完成全部工程的，厂家需付甲、丙两队共5500元.（1）求甲、乙、丙各队单独完成全部工程各需多少天?（2）若工期要求不超过15天完成全部工程,问可由哪队单独完成此项工程花钱最少?请说明理由.
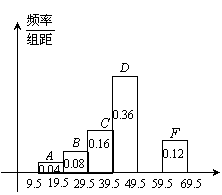25、（10′）为了解各年龄段观众对某电视剧的收视
率，某校初三（1）班的一个研究性学习小组，调查
了部分观众的收视情况并分成A、B、C、D、E、F
六组进行整理，其频率分布直方图如图所示，请回答：
（1）E组的频率为 ；若E组的频数
为12，则被调查的观众数为 人；
（2）补全频率分布直方图；
（3）若某村观众的人数为1200人，估计该村
50岁以上的观众有 人.
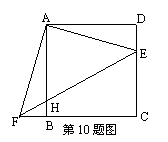
26、（12′）已知∠AOB=90°，OM是∠AOB的平分线,按以下要求解答问题:（1）将三角板的直角顶点P在射线OM上移动,两直角边分别与边OA、OB交于点C、D.①在图甲中证明:PC=PD.②在图乙中,点G是CD与OP的交点,且PG=PD,求△POD与△PDG的面积之比.（3）将三角板的直角顶点P在射线OM上移动,一直角边与边OB交于点D,OD=1,另一直角边与直线OA,OB分别交于点C、E,使以P、D、E为顶点的三角形与△OCD相似,在图丙中作出图形,并求OP的长.
