初二数学《一次函数》综合练习
考试时间：120分钟 总分：100分 命题人：许树荣 2007、6、2
一．精心选一选：（本大题共12题，每小题3分，共36分）：相信自己有能力选得又快又准，每道小题四个选择支中只有惟一一个是正确的，请将正确答案的代号填入下表。
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
|
|
1．骆驼被称为“沙漠之舟”，它的体温随时间的变化而变化，在这一问题中，自变量是 （ ）
A.沙漠 B.体温 C.时间 D.骆驼
2．下面两个变量是成正比例变化的是 ( )
A． 正方形的面积和它的边长． B． 变量x增加,变量y也随之增加;
C． 矩形的一组对边的边长固定,它的周长和另一组对边的边长．
D． 圆的周长与它的半径．
3． 下面哪个点不在函数y=－2x+3的图象上 （ ）
A．（-5，13） B．（0.5，2） C．（3，0） D．（1，1）
4．在函数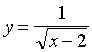
中，自变量
的取值范围是 （ ）
A． x≥2 B． x>2 C． x≤2 D． x<2
5．已知点（-4，y1），（2，y2）都在直线y= - x+2上，
则y1 y2大小关系是 ( )
A． y1 > y2 B． y1 = y2 C．y1 < y2 D． 不能比较
6．下列各图给出了变量x与y之间的函数是 （ ）
初一数学第一页（共6页）
7．直线y=kx＋b经过一、二、四象限,则k、b应满足 ( )
A． k>0, b<0 B． k>0, b>0 C． k<0, b<0; D． k<0, b>0
8．关于函数
，下列结论正确的是
（ ）
A．图象必经过点（﹣2，1） B．图象经过第一、二、三象限
C．当
时，
D．
随的增大而增大
9．已知一次函数y= ax+4与y = bx-2的图象在x轴上相交于同一点,
则
的值是 ( )
A．4 B．-2 C． D． -
 |  |  |  | ||||
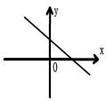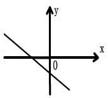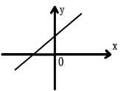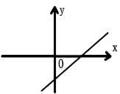10．已知一次函数y=kx+b,y随着x的增大而减小,且kb<0,则在直角坐标系内它的大致图象是 ( )
A． B． C． D．
11．小明骑自行车上学，开始以正常速度匀速行驶，但行至中途自行车出了故障，只好停下来修车。车修好后，因怕耽误上课，他比修车前加快了骑车速度匀速行驶。下面是行驶路程s(米)关于时间t(分)的函数图像，那么符合这个同学行驶情况的图像大致是 （ ）
 |
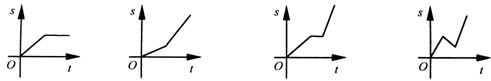A B C D
A． B． C． D．
12．已知函数y= -x+m与y= mx- 4的图象的交点在x轴的负半轴上那么m的值为 （ ）
A．±2 B．±4 C．2 D． -2
二．细心填题: （本大题共6个小题；每小题3分，共18分．）
你一定有能力把答案写在横线上
13．若一次函数
是正比例函数，则
的值为 。
初一数学第二页（共6页）
14．一次函数y=-3x+6的图象与x轴的交点坐标是 ，与y轴的交点坐标是 。
15．设地面（海拔为0km）气温是200C，如果每升高1km，气温下降60C， 则某地的气温t（0C）与高度h（km）的函数关系式是 。
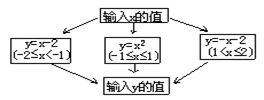16．根据右图所示的程序计算变量y
的值，若输入自变量x的值为
，
则输出的结果是_______。
17．小明根据某个一次函数关系式填写
了右表:其中有一格不慎被墨汁遮住了,
想想看，该空格里原来填的数是__________。
18．若函数y=-x-4与x轴交于点A，直线上有一点M，若△AOM的面积为8，
则点M的坐标 ．
三． 解一解: (本大题共8小题，共计46分)
通过认真思考，你完全有把握把下列各题解答完整
18. （本题6分）在同一坐标系内画出一次函数y1=-x+1 与y2=2x-2的图象， 并根据图象回答下列问题：
（1）.写出直线y1=-x+1 与y2=2x-2的
交点坐标
（2）.直接写出，当x取何值时
y1 ＜y2
19.（本题5分）已知直线
平行于直线y=-3x+4，且与直线y=2x-6的交点在x轴上，求此一次函数的解析式。
初一数学第三页（共6页）
20.（本题5分）已知函数y=(2m+1)x+m -3
(1)若这个函数的图象经过原点,求m的值
(2)若这个函数的图象不经过第二象限,求m的取值范围.
21．（本题6分） 如图是某汽车行驶的路程S(km)与时间t(min)
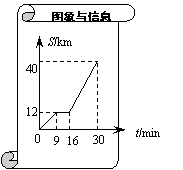的函数关系图.观察图中所提供的信息，
解答下列问题：
（1）汽车在前9分钟内的平均速度是多少？
（2）汽车在中途停了多长时间？
（3）当16≤t≤30时，求S与t的函数关系式.
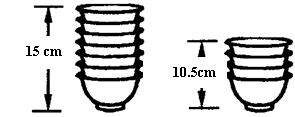
22．（本题6分）两摞相同规格的饭碗整齐地叠放在桌面上，请根据图中给出的数据信息，解答问题：
(1)求整齐叠放在桌面上饭碗的高度y(cm)与饭碗数x (个)之间的一次函数解析式(不要求写出自变量x的取值范围)；
(2 )若桌面上有12个饭碗，整齐叠放成一摞，求出它的高度。
 |
初一数学第四页（共6页）
23．（本题7分）某房地产开发公司计划建A、B两种户型的住房共80套，该公司所筹资金不少于2090万元，但不超过2096万元，且所筹资金全部用于建房，两种户型的建房成本和售价如下表：
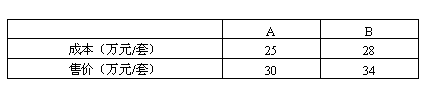
（1）该公司对这两种户型住房有哪几种建房方案？
（2）该公司如何建房获得利润最大？
（3）根据市场调查，每套B型住房的售价不会改变，每套A型住房的售价将会提高a万元（a>0），且所建的两种住房可全部售出，该公司又将如何建房获得利润最大？
注：利润=售价－成本
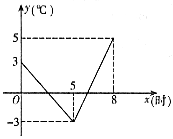
24．（5分）春、秋季节，由于冷空气的入侵，地面气温急剧下降到0℃以下的天气现象称为“霜冻”。由霜冻导致植物生长受到影响或破坏的现象称为霜冻灾害。
某种植物在气温是0℃以下持续时间超过3小时，即遭受霜冻灾害，需采取预防措施。下图是气象台某天发布的该地区气象信息，预报了次日0时～8时气温随时间变化情况，其中0时～5时，5时～8时的图像分别满足一次函数关系。请你根据图中信息，针对这种植物判断次日是否需要采取防霜冻措施，并说明理由。
初一数学第五页（共6页）
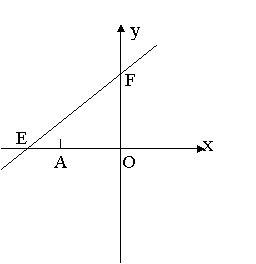
25．（本题8分）如图,直线y = kx+6与x轴y轴分别相交于点E,F.
点E的坐标为(- 8, 0), 点A的坐标为(- 6,0). 点P（x,y）是第二象限内的直线上的一个动点。
(1).求K的值；
(2).当点P运动过程中，试写出△OPA的面积S与x的函数关系式，并写出自变量x的取值范围；
(3).探究：当P运动到什么位置（求P的坐标）时，△OPA的面积为27／8，并说明理由
 |
初一数学第一页（共6页）