初二数学初中期末考试试卷
滨湖区教研中心
注意事项及说明：本卷考试时间为90分钟，满分为100分．卷中除要求近似计算的结果取近似值外，其余的结果应给出准确值．
一、细心填一填(共16个空，每空2分，共32分)
1. 16的平方根是 ， 64的立方根是 ，
= ．
2. 函数y=
中的自变量x 的取值范围是
3． 点P（－3 ，5）关于x 轴的对称点Ｑ的坐标是 ，点Ｐ到y轴的距离为 ．
4 ．已知实数
，
满足︱y－
︱+
=0， 则xy=
．
5．化简：
= ， （
）（
） = ．
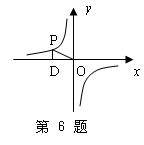
6．如图，点P是反比例函数
图象上的一点，PD⊥轴于点D，
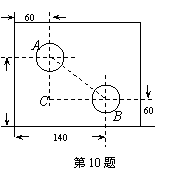若点Q（３，－２）也在该函数的图象上，则k=
，
△POD的面积= ．
|
合条件的平移变换过程： ．
8．在比例尺为１∶200 000的交通图上，距离为15厘米的两地之间的
实际距离约为 千米．
9．如图是一个外轮廓为矩形的机器零件平面示意图，根据图标出的
尺寸（单位：mm）计算两圆孔中心A和B的距离为 mm．
10．一棵树在太阳光下的影子长是9米，而在同一时刻身高1．6米的小江同学，影子长是1．2米，这棵树的高度是 米．
11．一组数据a， b， c， d， e 极差和方差分别是4和2，则数据 3a+2 ，3b+2 ，3c+2
3d+2 ，3e+2的极差和方差分别是 ．
二、精心选一选(共7小题，每小题3分，共21分)
12. 
，3.14 ， 
，π， 
，
中无理数有---------------------------【 】
A、 2个 B、 3个 C、 4个 D、 5个
13. 下列二次根式中与
是同类二次根式的是-------------------------------------------【 】
A、
B、
C、
D、
14. 已知点P（m－1，2－m）在第四象限，则m的取值范围是 ---------【 】
A、m＜1 B、m＜2 C、1＜m＜2 D、m＞2
15.下列事件发生的机会从小到大排序正确的是 ----------------------------------------【 】
错误！未找到引用源。从一副（54张）扑克牌中随机抽出一张是红心；
错误！未找到引用源。同时掷两枚硬币，出现两个正面；
错误！未找到引用源。买一注彩票，结果中特等奖；
错误！未找到引用源。无锡６月份会下雨；
错误！未找到引用源。迎面开过来一辆汽车，牌号末位数字是奇数．
A、错误！未找到引用源。错误！未找到引用源。错误！未找到引用源。错误！未找到引用源。错误！未找到引用源。 B、错误！未找到引用源。错误！未找到引用源。错误！未找到引用源。错误！未找到引用源。错误！未找到引用源。 C、错误！未找到引用源。错误！未找到引用源。错误！未找到引用源。错误！未找到引用源。错误！未找到引用源。 D、错误！未找到引用源。错误！未找到引用源。错误！未找到引用源。错误！未找到引用源。错误！未找到引用源。
16. 某人沿坡度i＝1 ：7的斜坡面前进30米，则他上升的铅直高度为-----------【 】
A、
米 B、
米 C、3
米 D、21米
17.下列说法中，正确的是--------------------------【 】
A、有两条边对应成比例且有一个角相等的两个三角形相似
B、有两个角对应相等的两个三角形相似
C、正比例函数y=3x与反比例函数
的图象位于不同的象限
D、两组数据中，平均数越小，这组数据越稳定
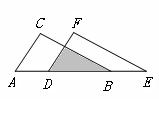
18.如图，把△ABC 沿 A－B 平移到△DEF 的位置，它们的重
叠部分（阴影部分）的面积是△ABC 的面积的一半，若AB =
，
则△ABC移动的距离是----------------------【 】
A、
－1 B、
C.、1 D、
三、认真答一答
19. 计算：（共2小题，每小题5分，共10分）
（1）
（2）
+ ６×tan30° + 
20. （本题共6分）
甲、乙两名射击运动员各进行10发子弹的射击，命中靶的环数如下表：
| 第几发 | 一 | 二 | 三 | 四 | 五 | 六 | 七 | 八 | 九 | 十 |
| 甲 | ８ | ６ | １０ | ８ | ７ | ９ | ７ | ４ | ５ | ６ |
| 乙 | ６ | ５ | ７ | ７ | ６ | ７ | ８ | ７ | ９ | ８ |
（１）在图中分别描出表示甲、乙命中靶的环数的折线图．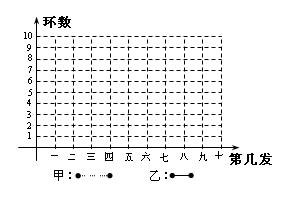
（甲用虚线连）
（２）求得：
甲命中靶的平均环数
甲＝ ，
方差S2甲＝ ；
乙命中靶的平均环数
乙＝ ，
方差S2乙= ．
（３）如果从甲、乙两名运动员中选一名参加比赛，你认为应选谁？请说明理由．
21.(本题共6分）
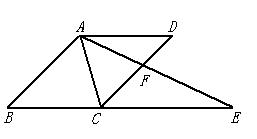
如图，ABCD是平行四边形，点E在边BC延长线上，连AE交CD于点F，如果∠EAC＝∠D．
试证明：AC·BE＝AE·AB．
22.（本题共6分）
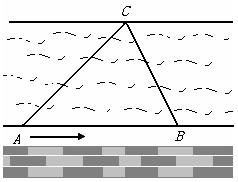
如图，小明沿着河岸边的人行道散步，想顺便测一测河的宽度，在A点，他发现对岸的一棵大树C与河岸的夹角∠CAB＝45o，继续往前走了2分钟到达点B，又测得∠ABC＝60o，已知他步行的平均速度是1米／秒．请你帮他算一算河的宽度（精确到0．1米）．
23. （本题共9分）
一般地，提高商品的单价，可以使每件商品获得更大的利润，但单价太高会反过来影响该商品的销售数量，只有通过合理的定价，才能取得较好的回报．小商品批发商李欣对其中一种小商品的单价与该种商品的日平均获利经过统计，得到下列数据：
| 该商品的销售单价x（元／件） | 1 | 1.7 | 1.9 | 2.4 |
| 该商品的日平均获利y（元） | 72 | 79 | 87 | 77 |
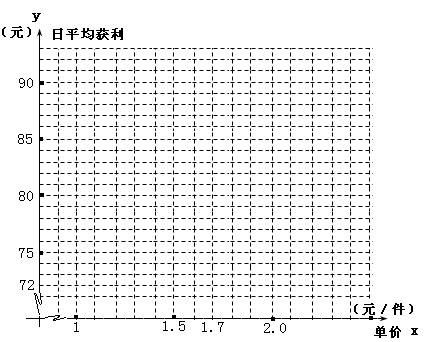
（1） 根据统计所得数据，在所给的平面直角坐标系中描出相应的各点。
（2） 用线段将题（1）所画的点从左到右顺次连接，若用此图象来模拟日平均获利y关于商品的销售单价x的函数关系，分别写出函数在 1．7≤x≤1．9和1．9≤x≤2．4 时的解析式；
（3）利用题（2）所得函数关系，当日平均获利不低于83元时，求该商品的销售单价 应该控制的范围．
24.（本题共10分）
直角梯形OABC中BC∥OA，在如图平面直角坐标系中，已知它的各顶点坐标分别是O（0，0），A（9，0），B（6，4），C（0，4）．点P从点C沿C—B—A运动，速度为每秒2个单位，点Q从A向O点运动，速度为每秒1个单位，当其中一个点到达终点时，另一个点也停止运动．两点同时出发，设运动的时间是t秒．
（1）点P和点Q 谁先到达终点？到达终点时t是多少？（请直接写出答案）
（2）当t取何值时，直线PQ∥AB ？并写出此时点Ｐ的坐标．（要写出解答过程）
（3）是否存在符合题意的t的值，使直角梯形OABC被直线PQ分成面积相等的两个部分？如果存在，求出t的值；如果不存在，请说明理由．
（4）探究：当t取何值时，直线PQ⊥AB ?（请直接写出答案，不需写出计算过程）．
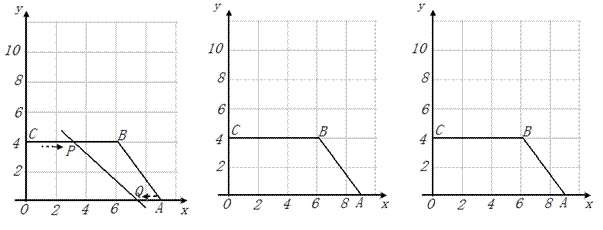图 １
图 ２（备用）
图 ３（备用）