专题1 不等式与方程
1、 某零件制造车间有工人20名,已知每名工人每天制造甲种零件6个或乙种零件5 个,且每制造一个甲种零件可获利润150元,每制造一个乙种零件可获利润260元.在这20名工人中,车间每天安排x名工人制造甲种零件,其余工人制造乙种
(1) 请写出车间每天所获利润y(元)与x(人)之间的函数关系式;
(2) 若要使车间每天所获利润不低于24000元,你认为至少要派多少名工人去制造乙种零件才合适
2、 某校科技夏令营的学生在3名老师的带领下,准备赴北京大学参观,体验大学生活,现有两家旅行社前来承包,报价均为每人2000元,他们都表示优惠:希望社表示带队老师免费,学生按8折收费;青春旅行社表示师生一律按7折收费,经核算,参加两旅行社的实际费用正好相等
(1) 该校参加科技夏令营的学生共有多少人?
(2) 如果又增加了部分学生,学校应选择哪家旅行社?
.3、乙两家旅行社为了吸引更多的顾客，分别提出了赴某地旅游的团体优惠方法，甲旅行社的优惠方法是：买4张全票，其余人按半价优惠；乙旅行社的优惠方法是：一律按7折优惠，已知两家旅行社的原价均为每人100元；那么随着团体人数的变化，哪家旅行社的收费更优惠？
4、 某饮料厂为了开发新产品,用A、B两种果汁原料各19㎏、17.2㎏.试制甲乙两种新型饮料共50㎏,下表是实验的相关数据
| 饮料 每千克含量 | 甲 | 乙 |
| A(单位:㎏) | 0.5 | 0.2 |
| B(单位:㎏) | 0.3 | 0.4 |
(1) 假设甲种饮料需配制x㎏,请你写出满足题意的不等式组,并求出其解集.
(2) 设甲种饮料每千克成本为4元,乙种饮料每千克成本为3元,这两种饮料成本总额为y元,请写出y与x的函数表达式.并根据(1)的运算结果,确定当甲种饮料配制多少千克时,甲乙两种饮料的成本总额最少?
5、在争创全国卫生城市的活动中，我市一“青年突击队”决定义务清运一堆重达100吨的垃圾．开工后，附近居民主动参加到义务劳动中，使清运垃圾的速度比原计划提高了一倍，结果提前4小时完成任务，问“青年突击队”原计划每小时清运多少吨垃圾？
6、4个男生和6个女生到图书馆参加装订杂志的义务劳动.管理员要求每人必须独立装订,而且每个男生的装订数是每个女生的2倍.在装订的过程中发现,女生们装订的总数肯定会超过30本,男、女生们装订的总数肯定不到98本.
问:男、女生平均每人各装订多少本?
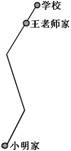
7、小明家、王老师家、学校在同一条路上，小明家到王老师家的路程为3千米，王老师家到学校的路程为0.5千米，由于小明的父母战斗在抗“非典”第一线，为了使他能按时到校，王老师每天骑自行车接小明上学。已知王老师骑自行车的速度是步行速度的3倍，每天比平时步行上班多用了20分钟，问王老师的步行速度及骑自行车速度各是多少千米/时？
 |
8、某校初一、初二两年级学生参加社会实践活动,原计划租用48座客车若干辆,但还有24人无坐位坐.
a) 设原计划租用48坐客车x辆,试用含x的代数式表示这两个年级学生的总人数;
(2)现决定租用60坐客车,则可比原计划租用48座客车少2辆,且所租60座客车中有一辆没有坐满,但这辆车已坐的座位超过36位.请你求出这两个年级学生的总数.
9、我市出租车在3km以内，起步价为12.5元，行程达到或超过3km后，每增加1km加付2.4元（不足1km亦按1km计价），昨天汪老师乘坐这种出租车从长城大厦到莲花北，恰巧沿途未遇红灯，下车时支付车费19.7元，问汪老师乘出租车走了多远的路？
10、如图所示：爬上小山有甲、乙两条石阶路. 运用所学统计知识解答下列问题：
(1)哪条路走起来更舒适？
(2)设计一条舒适的石阶路，简要说明理由。
 |
专题2 相似三角形
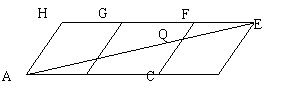
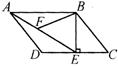
1、 如图,用三个全等的菱形ABGH,BCFG,CDEF拼成平行四边形ADEH,连接AE与BG,CF分别交于P,Q
(1) 若AB=6,求线段BP的长
(2) 观察图形是否有三角形与△ACQ全等?并证明你的结论.
 |
 | |||
|
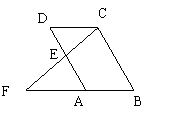
2、 如图四边形ABCD是平行四边形,点F在BA的延长线上,连接CF 交AD于点E
(1) 求证:△CDE∽△FAE
(2) 当E是AD的中点,且BC=2CD时,求证:∠F=∠BCF
 |
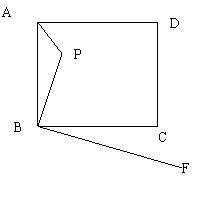3、如图,已知点P是边长为4的正方形ABCD内一点,且PB=3,BF⊥BP,垂足是B.请在射线BF上找一点M,使以点B,M,C为顶点的三角形与△ABP相似(请注意:全等图形是相似图形的特例)
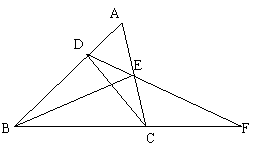
4.已知,如图,△ABC中,点D,E分别在边AB,AC上,连接DE并延长交BC的延长线于点F,连DC,BE.若∠BDE＋∠BCE=
（1）写出图中三对相似三角形(注意:不得添加字母和线)至少找两对。
（2）请在你所找出的相似三角形中选取一对,说明它们相似的理由.
 |
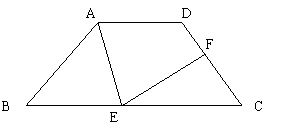
5、 如图，等腰梯形ABCD中，AD∥BC，AD=3㎝，BC=7㎝，∠B=
，P为下底BC上一点（不与B、C重合），连接AP，过P点作PE交DC于E，使得∠APE=∠B。
（1） 求证：△ABP∽△PCE
（2） 求等腰梯形的腰AB的长
（3）
在底边BC上是否存在一点P，使得DE：EC=5：3？如果存在，求BP的长如果不存在，请说明理由。
6、如图，在平行四边形ABCD中，过点B作BE⊥CD，垂足为E，连结AE．F为AE上一点，且∠BFE＝∠C．
(1)求证：△ABF∽△EAD；
(2)若AB＝4，∠BAE＝30°，求AE的长；
(3)在（1）、（2）的条件下，若AD＝3，求BF的长．（计算结果可含根号）
 |
1、 如图所示，已知：点D在△ABC的边AB上，连结CD，∠1=∠B，AD=4,AC=5,
求 BD的长.（6分）
2、如图在平面直角坐标系中，A点坐标为（8，0），B点坐标为（0，6），
点C是线段AB的中点。请问在x轴上是否存在一点P，使得以P、A、C为顶点的三角形与△AOB相似？若存在，求出P点坐标(写出计算的过程)；若不存在，说明理由。（7分）
 |
B
C
O
A
