参数法在相似形中的应用

参数法在相似形中的应用

一、已知线段倍数关系时，设其中一条线段长为参数

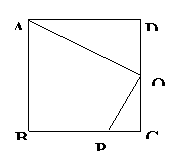例1. 已知：如图，在正方形ABCD中，P是BC上的点，且BP=3PC，Q是CD的中点，求证：△ADQ∽△QCP。（2001年河北省中考题）

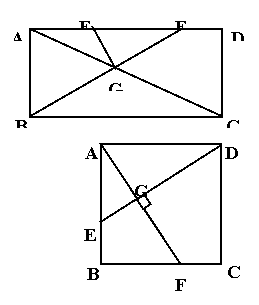
例2. 已知：如图，在矩形ABCD中，AD=3AB，AE=EF=FD，AC与BF相交于G，求证：EG⊥FB。

二、已知线段比设单位长为参数

例3. 如图，在正方形ABCD中，点E在AB边上，

且AE：EB=2：1，AF⊥DE于G，交BC于F，则

△AEG的面积与四边形BEGF的面积之比为（ ）

A. 1：2 B. 1: 4 C. 4: 9 D. 2: 3（2000年黄冈市中考单项选择题）

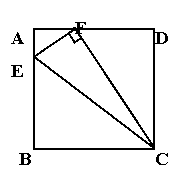
例4. 已知：如图4，ABCD是一矩形纸片，E是AB上一点，且AE：EB=3：5，EC=，把△BCE沿折痕EC向上翻折，若点B恰好落在边AD上的F点，求AB、BC的长各是多少？

三、挖掘题目中隐含的线段设参数

A

例5. 如图5，△ABC中，AD=1，DC=2，AB=4，E是AB上一点，且△DEC的面积等于△ABC面积的一半，则EB的长为___________。（2000年重庆市中考题）

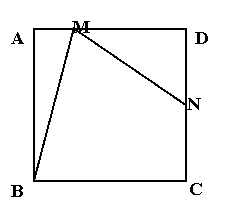例6. 如图，在正方形ABCD中，N是DC的中点，M是AD上异于D的点，且∠NMB=∠MBC，求的值。

A

练习题：已知：如图7，△ABC中，∠C=90°，D为AB上一点，作DE⊥BC于E，若BE=AC，BD=，DE+BC=1，求证：∠ABC=30°。

相似形自我测试题（B卷）

（时间60分钟 满分100分）

一. 填空题：（第2、4题6分，其余每小题4分，共36分）

1、若，则＿＿＿＿＿＿＿＿＿　

2、已知：x∶y∶z=3∶4∶5，且x+y-z=6，

则x=_______,y=_______，z=___________．

3、已知C是线段AB的黄金分割点，且AB=m，

则BC=____．

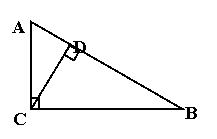
4、如图，已知在Rt△ABC中，∠ACB=90°,

CD⊥AB于D，AD＝p，DB＝q，则AC²＝＿＿＿＿；

BC²＝＿＿＿＿＿；CD²＝＿＿＿＿＿＿＿。

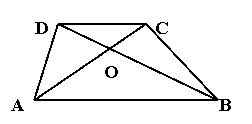
5、已知AB、CD为梯形ABCD的底，对角线

AC、BD的交点为O，且AB=12cm，CD=4cm，

BD=15cm，则OB=____，OD=______；

6、两个相似三角形的面积比为4∶2.25，若大三角形的周长为16厘米，则小三角形的周长为_____；

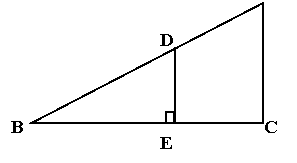
7、如图，矩形DEFG内接于△ABC，DE∶DG=3∶5，

若矩形的面积为60cm²，△ABC的高AM为10cm，

则△ABC的面积S＝＿＿＿＿＿＿。

二. 选择题：

1、下列四组图形中，不一定相似的是　　　　　　　　　　　　 　　 [　　]
A.邻边之比相等的两个矩形

B.有一个角相等的两个菱形

C.有一个角相等的两个等腰梯形

D.两条对角线的比相等，且夹角相等的两个平行四边形
2、如图，∠CAB=∠CBD，AB=4，

AC=6，BD=7.5，BC=5，则CD的长为[　　]

A.4　 B.5.5　 C.6　 D.6.25

3、两个相似多边形的相似之比为2：3，它们的面积和为78cm²，则较大的多边形的面积是　　　　　　　　　　　　　　　　　　　　　　　［　　］ A、54cm²　　　B、42 cm²　　　C、56 cm²　　　　D、52 cm²

4、如图，E为平行四边形ABCD的边AB的中点，且

，EF、AC相交于G，则［　　］ 　

A.5 　　　B.4 　　　　C.3 　　　D.2

5、△和△中，∠=∠，，则∠与∠的关系为(　　)

A.相等　　　　 B.互补　　C.相等或互补 　D.既不相等也不互补

三. 证明题：（第1题6分，第2～5题每题10分，共46分）

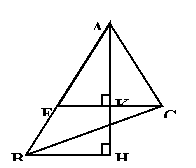
1、如图，在△ABC中，AE=AC，AH⊥CE，垂足为K，BH⊥AH，垂足为H．求证：△ABH∽△ACK

2、已知：△ABC中，AD是∠BAC的外角平分线，交BC的延长线于D．求证：

3、已知：在△ABC中，AD⊥BC于D，垂足D在B与C之间，且AB²=BD·BC，求证：∠BAC=90°

4、在△ABC中，∠ACB=90°，以AC为边向外作正方形ACDE，BE交AC于F，FG∥BC交AB于G．求证：CF=FG

5、梯形ABCD中，AD∥BC，E、F分别在AB、CD上，且EF∥AD，ED∥BF．求证：梯形AEFD∽梯形EBCF