初二2007级期末数学练习题（一）
班级: 姓名:
一、选择题：
1、函数
的自变量x的取值范围是（ ）
A、x≤-1 B、x≥-1 C、x≥-1 且x≠0、 D、x≤-1且x≠0
2、已知菱形的边长为6cm ,
一个内角为60°，则菱形较长的对角线长是（ ）
A、6cm B、
cm C、3cm D、
cm
3、如图，梯形ABCD，AB∥CD，E是AD的中点，EF∥CB
交AB于F，BC=4cm，则EF的长等于（ ）
A、1.5cm B、2cm C、2.5cm D、3cm
4、为适应国民经济持续快速协调发展，自2004年4月18日起，全国铁路实施第五次提速，提速后，火车由天津到上海的时间缩短了7.42小时，若天津到上海的路程为1362千米，提速前火车的平均速度为x千米/时，提速后火车的平均速度为y千米/时，则x、y应满足的关系是（ ）
A、
B、
C、
D、
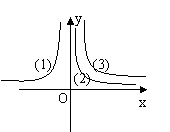
5、如图是三个反比例函数（1）
（2）
（3）
在x轴上方的图象，由此观察得到
k1、k2、k3的大小关系为（ ）
A、k1 >k2 >k3 B、k3> k2 > k1
C、k2> k3 > k1 D、k3 > k1 > k2
6、在⊿ABC中，AB=15，AC=13，高AD=12，则⊿ABC的周长为（ ）
A、42 B、32 C、42或32 D、37或33
7、某班七个合作学习小组人数如下：5、5、6、x、7、7、8，已知这组数据的平均数是6，则这组数据的中位数是（ ）
A、7 B、6 C、5.5 D、5
8、化简：
的结果是（ ）
A、
B、
C、
D、a+b
9、若一直角三角形两条边长为12和5，则第三边长为（ ）
A、13 B、13或
C、13或15 D、15
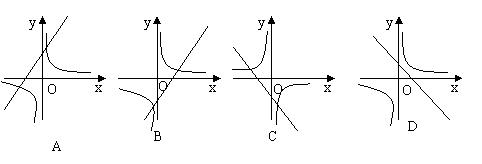10、在同一坐标系中，函数
和y=kx+1的图象大致是（ ）
二、填空题：
11、若反比例函数的图象经过点（3，-4），则此函数的解析式为
。
12、甲、乙两人进行射击比赛，在相同条件下各射击10次，他拉的平均成绩均为7环，10次射击成绩的方差分别是：s2甲=3，s2乙=1.2，，则成绩较稳定的是 （填“甲”或“乙”）
13、矩形ABCD中，对角线AC、BD相交于点O，∠AOB=2∠BOC，若AC=18cm，则
S矩形ABCD= cm。
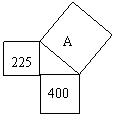
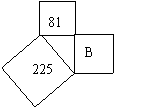
14、如图，图中正方形A的面积是 ，图中正方形B的面积是 。
 | |||
 |
4题图 5题图
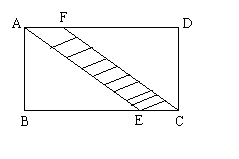
15、如图，有一条小路穿过长方形的草地ABCD，若
AB=10cm，BC=84cm，AE=100cm，则这条小路的面积是 m2。
16、如图，Rt⊿ABC中 ,BC是斜边，将⊿ABP绕点A逆时针旋转后，能与⊿ACP’重合，如果AP=3，由此可算出PP’= 。
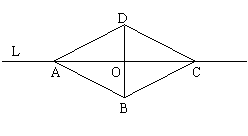
17、如图，直线l是四边形ABCD的对称轴，若AB=CD，有下面的结论：（1）AB∥CD；（2）AC⊥BD；（3）AO=OC；（4）AB⊥BC。其中正确的结论有 。
 |  | ||
16题图 17题图
18、近视眼镜的度数y（度）与镜片焦距x（米）成反比例，已知400度近视眼镜片的焦距为0.25米，则眼镜度数y与镜片焦距x之间的函数关系式为 。
三、解答题：
19、化简：
20、当k为何值时，关于x的方程
的解不大于13？
21、某班40名学生的某次数学测验成绩统计如下：
| 成绩（分） | 50 | 60 | 70 | 80 | 90 | 100 |
| 人数（人） | 2 | x | 10 | y | 4 | 2 |
（1） 若这个班的数学平均成绩是69成，求x和y的值；
（2） 设此班40名学生成绩的众数为a，中位数为b，求（ a-b）2的值；
（3） 根据以上信息，你认为这个班的数学水平怎么样？
 |
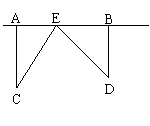22、为了丰富少年儿童的业余生活，某社区要在如图
所示AB所在的直线上建一图书室，本社区有两所学
校所在的位置在点C和点D处，CA⊥AB于A，DB⊥AB
于B。已知AB=25km，CA=15km，DB=10km。试问：图书
室E应建在距点A多少km处，才能使它到两所学校的
距离相等？
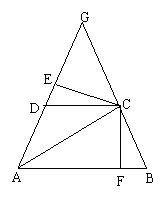23、如图，梯形ABCD中，AB∥DC，AD=DC=CD，AD、BC的延长线相交于G，CE⊥AB于F，
（1）请写图中5组相等的线段（已知的相等线段除外）
（2）选择（1）中你所写出的一组相等线段，说明它们相等的理由。
24、某气球内充满了一定质量的气体，当温度不变时，气球内气体的气压P（千帕）是气球体积、V（m3）的反比例函数，其图象如图所示（千帕是压强的一种单位）
（1）写出这个函数的解析式；
（2）当气球的体积为0.8立方米时，气球内的气压是多少千帕？
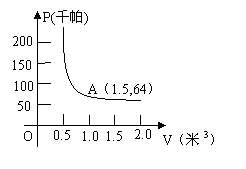（3）当气球内的气压大于144千帕时，气球将爆炸，为了安全起见，气球的体积应不小于多少立方米？
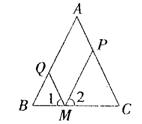
25．（8分）已知，在△ABC中，AB＝AC＝a，M为底边BC上任意一点，过点M分别作AB、AC的平行线交AC于P，交AB于Q。
⑴求四边形AQMP的周长；
⑵M位于BC的什么位置时，四边形AQMP为菱形？说明你的理由。
