八年级下学期期末测试题
一、填空题（每小题3分，共30分）
1、在平面直角坐标系中，点P（－1，2）关于y轴的对称点为
．
2、
的立方根是
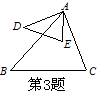
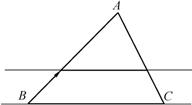
3、如图，已知∠DAB =∠CAE，请你添加一个适当的条件，使△ADE∽△ABC，你添加的条件是 ．
4、矩形长8cm，宽4cm，与该矩形面积相等的正方形的边长是 cm.
5、某公园的儿童游乐场是两个相似三角形地块，周长分别为
，它们的面积之和为
，则其中较大三角形的面积为
6、点P（3－a，5－a）是第二象限的点，则
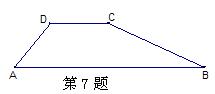
7、如图，一水坝的横断面为梯形ABCD，坝顶DC宽5m，斜坡AD=6m，∠A=600，斜坡BC的坡度i=1：2．则坝底AB的长= m（精确到0.1m）
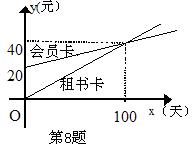8、某图书馆开展两种方式的租书业务：一种是使用会员卡，另一种是使用租书卡，使用这两种卡租书，租书金额y（元）与租书时间χ(天） 之间的关系如下图所示。当租书时间为120天时，应采用
方式比较合算。
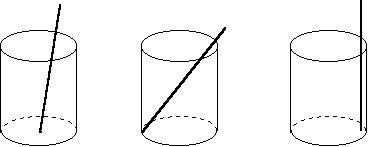
9、如图将一根长24cm的筷子，置于底面直径为5cm，高为12cm的圆柱形水杯中，设筷子露出在杯子外面长为hcm，则h的取值范围是
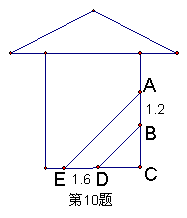10、如图，阳光通过窗口照到室内，在地面上留下1.6m宽的亮区DE，已知亮区一边到窗下的墙脚距离CE=3.6m，窗高AB=1.2m，那么窗口底边离地面的高度BC= m
．
二、选择题（每小题3分，共30分）
11、下列计算正确的是（ ）
A、
B、
C、
D、
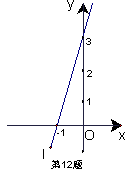12、如图，在直角坐标系中，直线l所表示的一次函数是（ ）
A、y=3x+3 B、y=3x－3 C、y=－3x+3 D、y=－3x－3
13、一个布袋里有2个红球和2个蓝球，第一次从布袋中摸出一个球，放回后第二次再摸出一个球，则两次摸出的球中发生的机会最大的是（ ）
A、两个红球 B、两个蓝球 C、一红一蓝 D、以上均错
14、样本X1、X2、X3、X4的平均数是
，极差是r，则样本X1+3，X2+3，X3+3，X4+3的平均数和极差分别是（ ）
A、+3，r+3 B、+3，r C、， r+3 D、， r
15、学校举行小发明比赛，小明要做一个直角三角形木架，现有长为30cm和40cm的两根木条，那么第三根木条的长应为（ ）cm ．
A、 50 B、 
C、 50或 D、50或
16、有下列说法：①有理数和数轴上的点一一对应；②
是3的平方根；③若∠A为锐角，且tanA=
，则∠A <
；④若A（a，m）、B（a+1，n）（a<0）在反比例函数
的图象上，则n<m．其中正确的有（ ）个
A、1 B、2 C、3 D、4
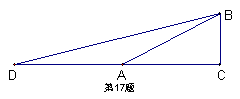
17、如图，在ΔABC中，∠C=900，延长CA至D，使AD=AB，∠BAC=300，则由图可得cot150的值是（ ）
A、
B、
C、
D、
18、如图，在长为8cm，宽为6cm的矩形中，截去一个矩形（图中阴影部分），如果剩下的矩形与原矩形相似，那么剩下矩形的面积是（ ）
A、 28cm2 B、 27cm2 C、21cm2 D 、 20cm2
19、在等腰△ABC和等腰△DEF中，∠A与∠D是顶角，下列判断正确的是（ ）
①∠A=∠D时，两三角形相似； ②∠A=∠E时，两三角形相似；
③
时，两三角形相似； ④∠B=∠E时，两三角形相似。
A、1个 B、2个 C、3个 D、4个
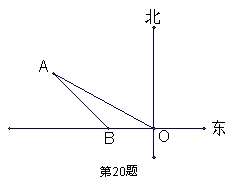
20、如图，某轮船在点O处测得一个小岛上的电视塔A在北偏西600的方向，船向西航行20海里到达B处，测得电视塔A在船的西北方向，若要轮船离电视塔最近，则还需向西航行（ ）
A、
B、
C、
D、
三、解答题（6小题，共60分）
21、（本题8分）计算：
22、（本题8分）八年级一、二班举行投篮比赛，每班各挑选10名同学代表班级参加7轮积分赛，投篮命中率如下：
| 场次 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 一班 | 85% | 88% | 77% | 75% | 85% | 80% | 70% |
| 二班 | 90% | 85% | 70% | 80% | 60% | 83% | 92% |
你认为哪个班级的投篮命中率较稳定？为什么？
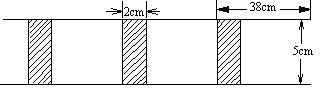23、（本题10分）将长为38cm，宽为5cm的长方形白纸，按如图所示方法粘合在一起，粘合部分白纸为2cm。
（1） 求10张白纸粘合后的长度；
（2） 
设x张白纸粘合后的总长为ycm，写出y与x的函数关系式。
24、（本题10分）升国旗活动时，某同学站在距旗杆27米的地方，当五星红旗冉冉升起时，同学行注目礼，五星红旗升至旗杆顶端时测得该同学视线的仰角为30°，已知该同学身高1.5米，你能计算出旗杆的高度吗？请你先画出示意图，再写出计算过程（结果用根式表示）。
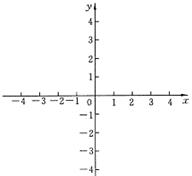
25、（本题12分）如图，在△ABC中，AB＝7，AC＝6，BC＝8.线段BC所在直线以每秒2个单位的速度沿BA方向运动，并始终保持与原位置平行.记x秒时，该直线在△ABC内的部分的长度为y.试写出y关于x的函数关系式，并在直角坐标系中画出这一函数的图象.
26、（本题12分）
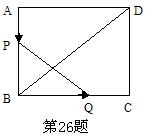已知矩形ABCD，长BC=12cm，宽AB=8cm，P、Q分别是AB、BC上运动的两点。若P自点A出发，以1cm/s的速度沿AB方向运动，同时，Q自点B出发以2cm/s的速度沿BC方向运动，问经过几秒，以P、B、Q为顶点的三角形与△BDC相似？
2005-2006学年度第二学期期末练习2
一、填空：（本大题共12小题，每空2分，共2 6分）
1、
的相反数是 。
2、9的平方根是 。
3、点A（－1，2）关于原点对称的点的坐标是___ __。
4、函数
中，自变量
的取值范围是 。
5、写出一个图象经过点
的函数的解析式
。
6、计算：
。
7、分解因式：
。
8、相似三角形对应边的比为2：3，则它们对应高的比为 ，它们面积的比为 。
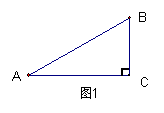
9、如图1，在Rt
中，
，则
。
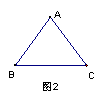10、如图2，在等腰△ABC中，AB=AC=5，BC=6，则△ABC的面积为
。
11、在RtΔABC中，∠C＝90º，若sinA=
, 则tanB=
12、。某次数学检测，从频数分布直方图中看出，落在50~60分的人数是20，频率是10%，则参加该次考试的总人数是 人。
二、选择题：（每小题4分，共20分）
13、下列各式计算正确的是 （ ）
A．
B． 
C ．
D． 
14、当
时，化简
的结果为（ ）
Ａ． 
Ｂ． 
Ｃ．
Ｄ．
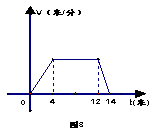
15、如图2所示的图象表示一辆汽车从出发到停止的行驶过程中速度（V）随时间（t）变化而变化的情况，下列判断错误的是（ ）
A、汽车从出发到停止共行驶了14分钟
B、汽车保持匀速行驶8分钟
C、出发后4分钟到12分钟之间汽车处于停止状态
D、汽车从减速行驶到停止用了2分钟
16、有下列一些事件：（1）抛一枚普通硬币，反面朝上 （2）在一副52张（无大小王）的普通扑克中抽出一张恰为红桃（3）掷一枚普通的正六面体色子所得的点数为奇数（4）从装有17个红球、2个白球的口袋中摸出一个球恰为白球的，其中等可能的是（ ）
A、（1）（2）（3） B、（1）（2）（4） C、（1）（3） D、（1）（2）（3）（4）
17、四个边长都为2cm的正方形按如图的位置摆放，
点A、B、C分别为三个正方形的中心，则图中三块阴影
部分的面积总和是（ ）
A．
B．
C．
D．无法确定
三、解答题：（本大题共5小题，每小题7分，共35分）
18、计算：
19、计算：
20、如图，为了测量某铁塔的高
，在距离
点
米的
点安置测角仪，测得点
的仰角
为
，已知测角仪的高
米，求铁塔的高（精确到
米）。
|
21、如图，已知AD=2，AE=3，AB=6，AC=4。
（1）
试证明△ADE和 △ACB相似；
（2） 若DE=1.5 求BC的长。
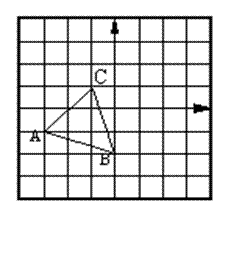22、将方格图中的△ABC作下列运动，分别画出相应的图形，并就其中一种变换指出三个顶点的坐标有什么变化？
(1) 将△ABC向右平移了3个单位得△A1B1C1，
点A1的坐标为 ；
(2) △ABC关于x轴对称的图形△A2B2C2，
点A2的坐标为 ；
四、解答题：
23、一次函数
图象经过点
和
。
（1）
试求
和
；
（2） 画出这个一次函数的图象；
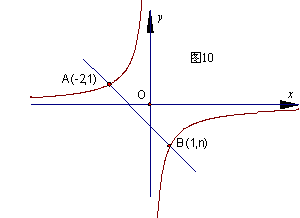24、如图，一次函数与反比例函数
的图象交于A、B两点，
（1） 利用图中条件求反比例函数和一次函数的解析式；
（2） 根据图象写出一次函数的值大于反比例函数值的的取值范围。
 |
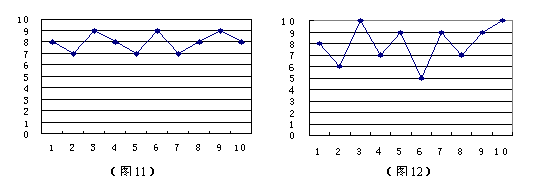25、甲、乙两名射手在相同条件下打靶，射中的环数分别如图11、图12所示：
（1）求甲、乙射中环数的平均数和方差。
（2）如果要从甲、乙两名射手中选一名去参加比赛，应选谁去？请说明你的理由。
25、如图，在△ABC中，BD、CE分别为三角形的两条高交于点O。
⑴问图11中有 个三角形与
相似；它们是
⑵连结DE,△ADE与△ABC是否相似，试说明理由。
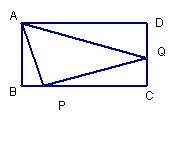
26、如图，在长方形ABCD中，AB=2，BC=4， Q是DC边的中点，P为一动点，若点P从A点出发，以1个单位/秒的速度沿着A→B→C→D方向运动。设从点A出发运动了秒，
（1）试分别写出当点P在AB、BC、CD上时，△AQP的面积
关于的函数关系式。
（2）问当取何值时，△AQP 是等腰三角形（至少求出一个值，每多求出一个值加2分）。
 |