八年级
 下学期期中数学试题
下学期期中数学试题
(总分:120分 时间:100分钟)

一、填空题(每小题2分,共24分)
1、![]() =
;
=
;
2、当![]() = 时,分式
= 时,分式![]() 的值为0;
的值为0;
3、已知直角三角形的两直角边长分别为3和4,则斜边长为 ;
4、学校到百色城的距离为5千米,则某同学骑自行车上街所用时间![]() 与速度
与速度![]() 的函数
的函数
关系式为 ;
5、命题“两直线平行,同位角相等”的逆命题是 ;
6、化简![]() 的结果是
;
的结果是
;
7、已知反比例函数![]() 的图象经过点(3,4),则
的图象经过点(3,4),则![]() =
;
=
;
|

|
![]()
|
R(Ω)之间的函数关系如右图所示,则I与R之间的函数
关系式是 ;
11、计算:![]() = ;
= ;
12、如下图,已知OA=OB,那么数轴上点A所表示的数是_______。
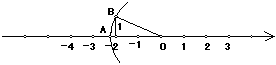 |
二、选择题(每小题2分,共16分)
13、以下列各组线段的长为边的三角形中,是直角三角形的是( )
(A) 2、3、4 (B) 3、4、5 (C) 4、5、6 (D)5、6、7
14、当分式![]() 有意义时,字母
有意义时,字母![]() 应满足( )
应满足( )
(A) ![]() (B)
(B) ![]() (C)
(C)
![]() (D)
(D)
![]()
15、反比例函数![]() 的图象经过点(
的图象经过点(![]() ,3),则它还经过点( )
,3),则它还经过点( )
(A)(6,![]() ) (B)(
) (B)(![]() ,
,![]() ) (C)(3,2) (D)(
) (C)(3,2) (D)(![]() ,3.1)
,3.1)
16、下列分式与分式![]() 相等的是( )
相等的是( )
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D)![]()
17、点![]() 、
、![]() 分别是反比例函数
分别是反比例函数![]() 上的两点,
上的两点,![]() ,则( )
,则( )
(A)
![]() (B)
(B) ![]() (C)
(C)![]() (D)无法确定
(D)无法确定
18、在同一直角坐标系中,正比例函数![]() 与反比例函数
与反比例函数![]() 的图象交点有( )
的图象交点有( )
(A) 3个 (B)2个 (C)1个 (D)0个
19、化简![]() 的结果是( )
的结果是( )
(A)![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D)
![]()
20、已知![]() ,则函数
,则函数![]() ,
,![]() 的图象可能是( )
的图象可能是( )
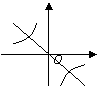
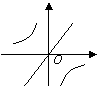


![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
(A) (B) (C) (D)
三、解答题(共60分)
21、计算(每小题5分,共10分)
(1)![]() (2)
(2)![]()
22、(6分)已知![]() 是
是![]() 的反比例函数,当
的反比例函数,当![]() =3时,
=3时,![]() =4,求当
=4,求当![]() =2时
=2时![]() 的值。
的值。
23、(6分)解方程:![]()
24、(6分)化简求值:![]() ,其中
,其中![]() ,
,![]()
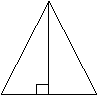 25、(7分)
25、(7分)![]() 中,
中,![]() ,
,![]() ,
,![]() 边上的高
边上的高![]() ,求
,求![]() 。
A
。
A
B D C
 26、(7分)A、B两种机器人都被用来搬运化工原料,A型机器人比B型机器人每小时多搬运30千克,A型机器人搬运900千克所用时间与B型机器人搬运600千克所用时间相等,两种机器人每小时各搬运多少化工原料?
26、(7分)A、B两种机器人都被用来搬运化工原料,A型机器人比B型机器人每小时多搬运30千克,A型机器人搬运900千克所用时间与B型机器人搬运600千克所用时间相等,两种机器人每小时各搬运多少化工原料?
27、(8分)小明家离学校的距离为2400![]() ,他骑自行车上学的速度为
,他骑自行车上学的速度为![]() (
(![]() /
/![]() ),所需时间
),所需时间![]() (
(![]() )。
)。
(1)写出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)如果小明骑车的速度最快为5![]() /
/![]() ,他至少需几分钟到校?
,他至少需几分钟到校?
(3)小明若用10![]() 到校,那么他骑车的平均速度是多少?
到校,那么他骑车的平均速度是多少?
|
|
|
 28、(10分)如图,已知直线
28、(10分)如图,已知直线(1)分别求直线ab及双曲线的解析式;
(2)已知点d的横坐标是 —2,求点d的坐标; d
![]() (3)根据图象,当
(3)根据图象,当![]() 在什么范围内取值时,
在什么范围内取值时,![]() ?
a o
?
a o ![]()