八年级数学第一学期教学质量检测试卷
| 题号 | 一 | 二 | 三 | 四 | 五 | 总分 |
| 得分 |
一、轻松入题选一选．本题共有10道小题，每小题3分，共30分．请把你认为唯一正确
的答案代号选出，填入题后的括号内．
1、已知点P位于y轴左侧和x轴上方，距y轴3个单位长度，距x轴4个单位长度，则点P的坐
标是( )
A、(3，4) B、(- 3，4) C、(4，3) D、(- 4，3)
2、若点P(a，b)在第四象限，则点Q(a，-b)在( )
A、第一象限 B、第二象限 C、第三象限 D、第四象限
3、下列各曲线中，不能表示y是x函数的是( )
4、全等的图形是 ( )
A、形状相同的两个图形 B、周长相等的两个图形
C、面积相等的两个图形 D、能够完全重合的两个图形
5、以下关于三角形的各种叙述中，错误的一个是( )
A、三角形的三条高至少有一条在三角形内
B、三角形的三个内角中至少有两个是锐角
C、两条边及其中以边对角对应相等的两个三角形全等
D、两条边相等的两个直角三角形不一定全等
6、在平面直角坐标系中P
(x，y)→P (x+2，y
-3)的平移过程是( )
A、向右平移2个单位，再向上平移3个单位
B、向右平移2个单位，再向下平移3个单位
C、向左平移2个单位，再向上平移3个单位
D、向左平移2个单位，再向下平移3个单位
7、若函数y=
- 2mx- (m-
4)的图象过原点，则m 的取值为( )
A、2 B、-2 C、2或-2 D、不确定
8、根据下列已知条件，能画出唯一ΔABC的是( )
A、AB=3，BC=4，CA=8 B、AB=4，BC=3，∠A=30°
C、∠A=60°，∠B=45°，AB=4 D、∠C=90°，AB=6
9、一次函数y=k x + b中，当x=1时，y=1；当x=2时，y=4．则k、b的值为( )
A、3，-2 B、-3，2 C、-2，3 D、-3，-2
10、已知一次函数y=kx- k，若y随x的增大而增大，则它的图象经过( )
A、第一、二、三象限 B、第二、三、四象限
C、第一、二、四象限 D、第一、三、四象限
二、快乐晋级填一填．本大题共10小题，每小题3分，共30分．
11、点P(a，b)在x轴的正半轴上，则ab= 
．
12、已知点P在第二象限，它的横坐标与纵坐标的和为3，则点P的坐标可以是
(写出
符合条件的一个即可)．
13、函数y= 
中，自变量x的取值范围是 
．
14、游泳池原有水300 m，现以每分钟10 m的速度向池内注水．已知池的容积为1500m，
则池内水量Q(m)与注水时间t(min)之间的函数关系是
，自变量t 的取值范
围是
．
15、下列函数：① y+x=0；② y= 
；③ y= - x；④ y= - 2x+1．
其中是一次函数的是 (填代号)．
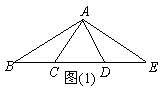
16、如图(1)，已知AC=CD=DA=CB=DE，则图
中共有
个等腰三角形．
17、在ΔABC 中，已知∠A=105°，∠B -∠C=15°，则∠C= ．
18、已知y=(m-3)x
是正比例函数，且y随x的增大而减小，则的值是
．
19、正比例函数y=
- kx的图象经过原点和第一、三象限，则直线y= kx+3不经过第
象限．
20、“两个锐角对应相等”(填“能”或“不能”)判定两个直角三角形全等．
三、挑战你的技能．每小题6分，共12分.
21、 如果点A(-3，2)，B(2a，a +1)都在函数y = x- b的图像上，求b、a的值．-5，- 4
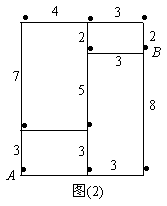
22、星期天，小明和爸爸一起从家(A点)去看望奶奶(B点)，如图(2)所示，他们所走的一条
路径可用(0，0)→(0，3)→(4，3)→(4，8)→(7，8)表示．
(1)用笔在图中描出小明和爸爸所走的这条路径；
(2)请你用数对写出另外的两条由到的路径，并判断这三种走法(包括给出的走法)的路
程是否相等．
四、试试你的推理．每小题分，共分．
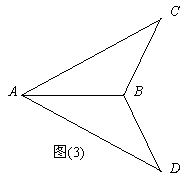
23、如图(3)，AC=AD，BC=BD，图中有相等的角吗？请你找出来，并说明理由．
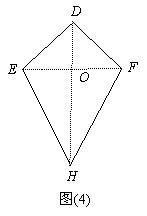
24、小明做作了一个如图(4)所示的风筝骨架，其中∠EDH=∠FDH，ED=FD．
(1)请你找出图中所有的全等三角形；
(2)请选择其中的一对，简要说明理由．
五、数学与我们的生活．第25题6分，26题8分，共14分．
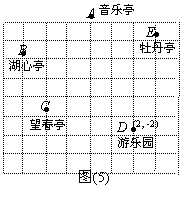
25、李明和爸爸、妈妈到世纪公园游玩，回到家后，他利用平面直角坐标系画出了公园
的景区地图，如图(5)，可是他忘记了在图中标出原点和x轴、y轴，只知道游乐园D的
坐标是(2，-2)，请你帮他画出坐标系并求出其他各景点的坐标．
26、在正常情况下，一个人在运动时所能承受的每分钟心跳的最高次数S(次/分)是这个人
年龄n(岁)的一次函数．
(1)根据以上信息，求在正常情况下，S关于n的函数关系式；
(2)若一位63岁的人在跑步，医生在途中给他测得10秒心跳为26次，问：他是否有危
险？为什么？