八年级数学阶段性评价试卷
班级 姓名 学号 得分
说明：（1）本卷的测试范围是浙教版八年级下册第三章：频数及其分布；
（2）本卷满分100分，测试时间为50分钟。
一、精心选一选（每题3分，共30分）：
1、样本频数分布反映了（ ）
（A）样本数据的多少； （B）样本数据的平均水平；
（C）样本数据的离散程度； （D）样本数据在各个小范围内数量的多少。
2、有一句地方民谣“早穿皮袄午穿纱”，说明此地气温的特点的特征数是（ ）
（A）平均数； （B）中位数； （C）极差； （D）众数。
3、在数据10，20，40，30，80，90，50，40，40，50中，极差是（ ）
（A）40； （B）70； （C）80； （D）90。
4、某中学教研组有25名教师，将他们的年龄分成3组，在28～35岁组内有8名教师，那么这个小组的频率是（ ）
（A）0.38； （B）0.32； （C）3.12； （D）0.12。
5、一组数据的最大值与最小值之差为80，若取组距为10，则组数一般是（ ）
（A）7； （B）8； （C）9； （D）10。
6、在英文字母was a sunny in park中,字母 n出现的频率是（ ）
（A）0.2； （B）0.3； （C）0.13； （D）0.22。
7、在样本12，8，14，6，10，13，15，9，11，16，8，12，14，9，13，5，8，11，7，10中，频率是0.3的组的范围是（ ）
（A）4.5～7.5； （B）7.5～10.5； （C）10.5～13.5； （D）13.5～16.5。
8、一组数据共40个，分成6组，第1～4组的频数分别是10，5，7，6，第5组的频率是0.10，则第6组的频率是（ ）
（A）0.15； （B）0.20； （C）0.25； （D）0.30。
9、将100个数据分成8组（如下表），则第6组的频数是（ ）
（A）12； （B）13； （C）14； （D）15。
| 组号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|
| 频数 | 11 | 14 | 12 | 13 | 13 | 12 | 10 |
810、某校九（1）班50名学生中考成绩的频数分布
直方图如图所示，则总分在600分以上的学生人数为（ ）
（A）20； （B）30； （C）35； （D）45。
二、细心填一填（每题3分，共30分）：
11、在对100个数据进行整理的频数分布表中，各组的频数之和等于 ，各组的频率之和等于 。
12、瑞安某日的最高气温是15℃，气温的极差为10℃，则该日的最低气温是 。
13、某校八年级（1）班共有55位同学，2月份出生的人数的频率是0.2，则该班2月份生日的同学有 人。
14、在数据6，9，11，8，7，11，12，10，9，10，12，10，9，8，13，15，10，11，12，13中，出现次数最多的数据是 。
15、荷兰著名数学家卢道夫早在1596年就推算出了具有15位小数的
值，的值是3.93，在这个数中，数字3出现的频率是
。
16、下表是某校八年级（1）班共50位同学身高情况的频数分布表，则表中的组距是 ，估计极差至多是 。
| 组别（cm） | 145.5～152.5 | 152.5～159.5 | 159.5～166.5 | 166.5～173.5 |
| 频数(人) | 9 | 19 | 14 | 8 |
17、在第16题中，频率是0.28的这一小组的组中值是 。
18、在第16题中，该班50名学生的平均身高是 cm（精确到0.01）。
19、将数据分成4组，画出频数分布直方图，各小长方形的高的比是1：3：4：2，若第2组的频数是15，则此样本的样本容量是 。
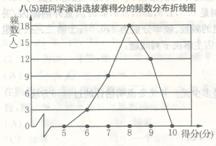20、如图是八（5）班演讲选拔赛得分情况的频数分布折线图，则分布在折线图两端的虚设组的范围分别是
。
三、认真做一做（本题共有4小题，共40分）：
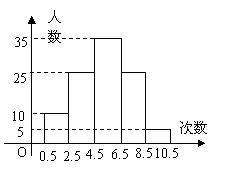21、（本题6分）：为了了解某初中学生的体能情况，抽取若干名学生在单位时间内进行引体向上测试，将所得数据整理后，画出频数分布直方图（如图4），图中从左到右依次为第1、2、3、4、5组。
（1） 求抽取了多少名学生参加测试？
（2） 处于哪个次数段的学生数最多？
（答出是第几组即可）
（3） 若次数在5次（含5次）以上为达标，
求这次测试的达标率。
22、（本题9分）：当今，青少年视力水平的下降已引起全社会的关注，为了了解某校八年级800名学生的视力情况，从中抽取一部分学生进行检测。
（1）补全频数分布表：
| 组别 | 3.95～4.25 |
| 4.55～4.85 | 4.85～5.15 | 5.15～5.45 |
| 频数 | 2 | 6 | 10 | 1 |
|
| 频率 |
| 0.12 |
|
|
|
（2）估算该校八年级800名学生的平均视力；
（3）对该校八年级青少年视力情况作出评价。
23、（本题9分）：如图是若干名学生每分钟脉搏跳动次数的频数分布折线图。
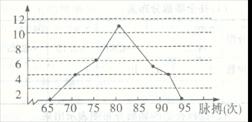（1）求学生的总人数；
（2）分布在两端虚设的两组的组中值分别是多少？
（3）估计样本的中位数。
24、（本题16分）：测量36名老人的血压，获得每位老人的舒张压数据如下（单位：毫米汞柱）：100，110，80，88，90，80，87，88，90，78，120，80，82，84，88，89，72，100，110，90，80，85，86，88，90，88，87，85，70，80，88，89，90，92，85，84。
（1）求这组数据的极差；
（2）按组距5毫米汞柱将数据分组，确定每组的组中值，列出频数分布表；
（3）画出频数分布直方图；
（4）画出频数分布折线图。