八年级数学期末整合卷（总分120分）
班级 姓名 成绩
一：选择题（每题2分，共32分）
1、 在 
中，分式的个数是（ ）
A、1 B、2 C、3 D、4
2、下列式中，与分式
的值相等的是（ ）
A、
B、
C、
D、
3、下列函数中，y是x的反比例函数的是（ ）
A、
B、
C、
D、
4、对于
，下列说法错误的是（ ）
A、图象在第一、三象限内B、图象经过（2，2）、（－2，－2）
C、y随x增大而减小 D、关于原点对称
5、如图，函数
与
在同一坐标系中，图象只能是下图中的（ ）
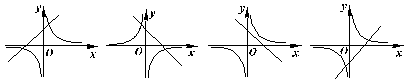
（A） （B） （C） （D）
6. 用科学计数法表示0.＝（ ）
A. 
B.
C.
D.
7. 在下列图形中，不是轴对称图形的有（ ）
A. 钝角 B.
正多边形 C.
平行四边形 D.
等腰三角形
8. 若双曲线
经过（a，－a）点，则a的值为（ ）
A. 2 B.
4 C.
D.
9.在平行四边形ABCD中，对角线AC与BD相交于点O，若AC=6，BD=8，则边AB的取值范围是( )
A.1﹤AB﹤7; B. 2﹤AB﹤14; C. 6﹤AB﹤8; D. 3﹤AB﹤4
10. 不能判定四边形ABCD为平行四边形的条件是( )
A.AB∥CD，AD=BC. B.
AB∥CD，∠A=∠C;
C. AD∥BC，AD=BC. D.
∠A=∠C，∠B=∠D.
11.在下列性质中，平行四边形不一定具有的是（ ）
A、对边相等 B、对边平行 C、对角互补 D、内角和为360°
12. 如图，在一个由4×4个小正方形组成的正方形网格中，阴影部分面积与正方形 ABCD的面积比是（ ） A、3：4 B、5：8 C、9：16 D、1：2
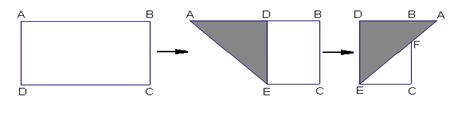
13．如图,有一矩形纸片ABCD,AB=10,AD=6,将纸片折叠，使AD边落在AB边上， 折痕为AE，再将△AED以DE为折痕向右折叠，AE与BC交于点F，则△CEF的 面积为（ ） A．4 B．6 C．8 D．10
14．在平行四边形ABCD中,∠B=110O,延长AD至F,延长CD至E,连接EF,则∠E+∠F=（ ） A、110O B、30O C、50O D、70O
15．如图，已知在梯形ABCD中，AD∥BC，E为CD的中点，若用S1、S2、S3分别表示△ABE、△ADE、△BCE、的面积，则S1、S2、S3的关系是（ ）
A、S1+S3﹥S2 B、S1+S3=S2 C、S1+S3﹤S2 D、不能确定
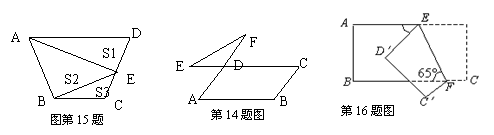16．如图,把一长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置，若∠EFB＝65°，则∠AED′等于（ ）A．50°B．55° C．60° D．65°
二．填空题（每题2分，共34分）
1、x、y满足关系_____________时，分式
无意义.
2、若分式方程
有增根，则增根为_____________.
3、函数
的图象在_____________象限内，在每一象限内y随x的增大而___________.
4、若反比例函数的图象过点（－2，－3）则其解析式为_____________.
5、若一个三角形的三边长之比为5∶12∶13，则最长边所对的角为_____________.
6、若直角三角形的两边长为6和8，则第三边长为_____________.
7. 菱形ABCD的周长为36，其相邻两内角的度数比为1:5，则此菱形的面积为_________；
8.直角梯形的两底分别为2和6，与底不垂直的腰长为5，则些梯形的面积为_________________;
9．如图，矩形ABCD中，O是对角线的交点，AE⊥BD于E，若OE﹕OD=1﹕2，AC=18cm，则AB=________
10.一梯形的两条对角线互相垂直，上、下底之和为3，则梯形两条对角线的平方和等于__________________;
11. 已知菱形ABCD的两条对角线AC=8cm，BD=6cm，那么对角线交点到任意一边的距离等于_______米.
12.如图，矩形ABCD中，AB=4，BC=2，E是DC上一点，∠BAC=∠EAC，则EC长为_________________;
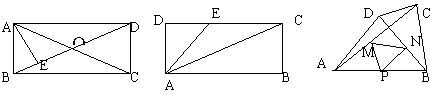
第(9)题 第(12题 第(13)题
13. 如图,在四边形ABCD中，AD=BC，∠DAB=50度，∠ABC=70度，若P、M、N分别是AB、AC、BD的中点，BC=8cm，那么△PMN的周长等于______;
14.已知菱形ABCD的边长为6，∠A=60°，如果点P是菱形内一点，且PB=PD=
那么AP的长为__ ___;
15. 直角三角形周长为2+
，斜边上的中线为1，那么其面积为_________;
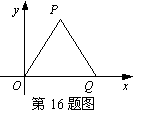
16. 如右图，△OPQ是边长为2的等边三角形，
若反比例函数的图象过点P，则它的解析式是_______。
17．在样本方差计算公式S2＝
[(x1—25)2+(x2—25)2+…+(x30—25)2]中数字25表示样本的__________________________。
三．计算与解答
1、（5分）解方程
（5分） 2化简求值：
，其中
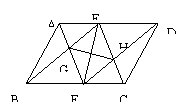2．（6分）如图，平行四边形ABCD中，E、F分别在AD、BC上，AE=CF，AF与BE交于G，CE与DF交于H，求证：EF与GH互相平分。
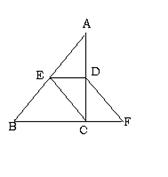
3、（6分）如图在△ABC中，∠BCA=90°，D、E分别是AC、AB的中点，点F在BC延长线上，∠CDF=∠A；
（1） 求证：四边形DECF是平行四边形；
（2） BC/AB=3/5，四边形EBFD的周长为22，求DE的长。
 | |
名称（或创意）__________________ 名称（或创意）
4、（6分）许多几何图形是优美的。对称，就是一种美。请你运用“二个圆、二个三角形、二条线段”在下图的方框内设计两幅轴对称图形，并用简练的文字说明这幅图形的名称（或创意）。
5、（12分）如图1，点A在反比例函数（x＞0）的图象上，B点在x轴上，且∠OAB = 90°，OA = AB，作AC⊥OB于C
.①（4分）求点A的坐标.
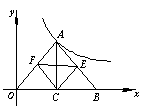
②取AB的中点E，作∠ECF = 90°交AO于F，试通过计算说明EF2与OF2+EB2的大小关系.
③如图2，过点C作∠ECF = 90°交AB于E，交AO于F，②中的结论是否仍成立？证明你的结论.
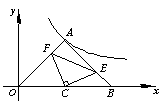
（图2）
6、（8分）如图所示，一根长2a的木棍（AB），斜靠在与地面（OM）垂直的墙（ON）上，设木棍的中点为P。若木棍A端沿墙下滑，且B端沿地面向右滑行。
（1）请判断木棍滑动的过程中，点P到点O的距离是否变化，并简述理由。
（2）在木棍滑动的过程中，当滑动到什么位置时，△AOB的面积最大？简述理由，并求出面积的最大值。
7（6分）如图，正方形网格中的每个小正方形边长都为1，每个小正方形的顶点叫格点，以格点为顶点分别按下列要求画三角形和平行四边形。
（1）使三角形三边长为3，
，
。
（2）使平行四边形有一锐角为45°，且面积为4。
|
|
（1） （2）
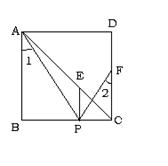8、（7分选做）已知：如图，在正方形ABCD中，F是CD边上的中点，点P在BC上，∠1=∠2，PE⊥BC交AC于点E，垂足为P。求证：AP=3PE。