八年级数学第十一章单元测试题

八年级数学第十一章单元测试题

一、填空题（每小题2分，共20分）

1、在圆的周长公式C=2πr中，变量是________，常量是_________.

2、在函数中，自变量的取值范围是_________.

3、若函数是正比例函数，则的值是　　　　　 .

4、若直线y=与直线y=3mx+6平行，则m=　　　　。

5、已知一次函数y＝kx＋5过点P（－1，2）则k=　　　

6、函数与轴交点坐标为__________，与轴交点坐标为__________,通过第__________象限，它与两坐标轴围成三角形面积为__________.

7、将直线y＝3x向下平移5个单位，得到直线　　　　　 ；将直线y＝-x-5向上平移5个单位，得到直线　　　　　 .

8、出租车收费按路程计算，3km内（包括3km）收费8元;超过3km每增加1km加收１元，则路程x≥3km时，车费y（元）与x (km)之间的函数关系式是________________．

9、对于一次函数，当_______时，图象在轴下方.

10、某商店出售一种瓜子，其售价（元）与瓜子质量（千克）之间的关系如下表

质量（千克）	1	2	3	4	……
售价（元）	3.60+0.20	7.20+0.20	10.80+0.20	14.40+0.2	……

由上表得与之间的关系式是 　　　　　　　　　　 .

二、选择题（每小题3分，共30分）

1、下列函数 (1) (2) (3)　(4)　(5)中，是一次函数的有（　　）　　　　

A、4个　　  B、3个　　　C、2个　　　D、1个

2、函数中自变量的取值范围是 （　　）

A、　　 B、　　  C、且　　D、且

3、在直线y=x+1上的点是（　　）

A、（1，-1）　　 B、（-1，-1）　　C、（2，3） 　　D、（0，-1）

4、一次函数y=-2x-3的图象经过第（　　）象限

A、一、二、三　　　B、一、二、四　　  C、一、三、四　　 D、二、三、四

5、函数y=x-8与y轴的交点坐标是（　　）

A、（0，-8）　　 B、（-8，0）　　 C、（2，0）　　 D、（0，2）

6、直线,,共同具有的特征是 （　　）

A、经过原点　　　　　　　　　　　  B、与轴交于负半轴

C、随增大而增大　　　　　　　  D、随增大而减小

7、函数y=(k-1)x，y随x增大而减小，则k的范围是　(　　)

A、　　　 B、 　　 C、　　　　D、

8、一辆汽车从江油以40千米/时的速度驶往成都,已知江油与成都相距约160千米,则汽车距成都的距离S(千米)与其行驶的时间(小时)之间的函数关系是 （　　）

A、　　　　　　　　 B、

C、　　　　　　  D、

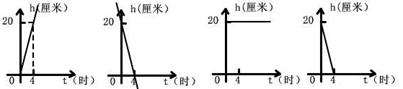9、一支蜡烛长20厘米, 点燃后每小时燃烧5厘米, 燃烧时剩下的高度(厘米)与燃烧时间 (时)的函数关系的图象是 （　　）

A　　　　　　  B　　　　　　　  C　　　　　　  D

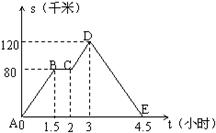10、如右上图中的图象（折线ABCDE）描述了一汽车在某一直线上的行驶过程中，汽车离出发地的距离（千米）和行驶时间（小时）之间的函数关系，根据图中提供的信息，给出下列说法：①汽车共行驶了120千米；②汽车在行驶途中停留了0.5小时；③汽车在整个行驶过程中的平均速度为千米/时；④汽车自出发后3小时至4.5小时之间行驶的速度在逐渐减少.其中正确的说法共有 (　　)

　 A、1个　　 B、2个　　　C、3个　　　D、4个

三、解答题

1、（6分）已知函数

(1)若函数的图象是经过原点的直线, 求的值.

(2)若这个函数是一次函数,且随着的增大而减小, 求的取值范围.

(3)若这个函数是一次函数,且图象不经过第四象限, 求的取值范围.

2、（6分）已知直线L与直线y=2x+1的交点的横坐标为2，与直线y=-x+2的交点的纵坐标为1，求直线L的解析式。

3、（6分）在同一直角坐标系中,

(1)作出函数和的图象.

(2)用图象法求不等式的解集.

4、（6分）已知：等腰三角形的周长为40cm。

⑴求等腰三角形的底边长ycm与xcm腰长之间的函数关系式（x为自变量）；

⑵写出自变量的取值范围；

⑶在直角坐标系中，画出该函数的图像。

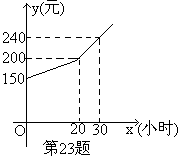5、（8分）为了鼓励小强勤做家务，培养他的劳动意识，小强每月的费用都是根据上月他的家务劳动时间所得奖励加上基本生活费从父母那里获取的。若设小强每月的家务劳动时间为x小时，该月可得（即下月他可获得）的总费为y元，则y（元）和x（小时）之间的函数图像如图所示。

（1）根据图像，请你写出小强每月的基本生活费为多少元；父母是如何奖励小强家务劳动的？

（2）写出当0≤x≤20时，相对应的y与x之间的函数关系式；

（3）若小强5月份希望有250元费用，则小强4月份需做家务多少时间？

6、（8分）某移动通讯公司开设了两种通讯业务①“全球通”：使用者先缴50元月租费，然后每通话1分钟时间，再付话费0.4元；②“快捷通”：不缴月租，每通话1分钟付话费0.6元，（本题的通话均指市内通话）。若一个月内通话x分钟，“全球通”和“快捷通”两种方式的费用分别为y₁元和y₂元。

⑴写出y₁、y₂之间的函数关系式；

⑵一个月通话多少分钟，两种移动通讯费用相同？

⑶某人估计一个月通话时间为300分钟，应选择哪种移动通讯合算些？

7、（10分）某服装厂现有A种布料70米，B种布料52米，现计划用这种布料生产M、N两种型号的时装80套。已知做一套M型号的时装需要A种布料0.6米，B种布料0.9米，可获利45元。做一套N型号的时装需要A种布料1.1米，B种布料0.4米，可获利50元。若设生产N型号的时装套数为x，用这种布料生产这两种型号的时装所获的总利润为y元。

（1）请写出满足题意的不等式组，并写出其解集。

（2）求y与x的函数关系式。

（3）该服装厂在生产这批时装中，当生产N型号的时装多少套时，所获利润最大？最大利润是多少？